Відношення і пропорції. Розв’язування задач прикладного характеру.

Про матеріал

Навчальний проект з математики "Відношення і пропорції. Розв’язування задач прикладного характеру". Даний проект розрахований для учнів 6 класу. Проект передбачає поділ класу на групи, кожна з яких протягом двох тижнів працює над своєю частиною роботи: збирає інформацію, підбирає цікаві факти, готує презентацію зі змістом опрацьованого матеріалу, робить висновки. Керівником проекту виступає вчитель. Всього формується 4 групи: історики, теоретики, практики, публіцисти. Даний проект об'єднує математику, географію, хімію, фізику.

Перегляд файлу

Навчальний проект з математики

Назва проекту: Відношення і пропорції. Розв’язування задач прикладного характеру.

Керівники проекту: Семенів О. Г., Пронтенко Л. О., Кучерук А. С.

Навчальні предмети: Математика

Клас: 6

Тип проекту: Дослідницький, творчий, пізнавальний

За кількістю учасників: Груповий

Приблизний час, необхідний для реалізації навчального проекту: Протягом одного або двох тижнів

Тематичне питання: Застосування знань з математики до розв’язування задач сюжетного змісту

Змістові питання:

Яка задача називається практичною
Які є види практичних задач в даній темі
Які практичні задачі з цієї теми може розв’язувати 6-ти класники

Мета та задачі проекту:

вивчити означення пропорції та відношення, основну властивість пропорції.
формувати навички розв'язування вправ на пропорції, уміння знаходити невідомий член пропорції;
розширити кругозір учнів, розвивати у них пізнавальну активність, логічне мислення;
виховувати зацікавленість предметом, почуття колективізму, відповідальність за одержання колективного результату роботи, впевненість у собі;
формувати економічну компетентність учнів.

Необхідне устаткування, приладдя та витратні матеріали: Комп’ютер, сканер, принтер, інтернет, процесори Microsoft Office (Word, Power Point, Publisher ) кольорові олівці, папір, учнівські зошити.

Вихідні знання та навички: Учні мають уявлення про задачі практичного змісту та застосовують знання з теми відношення і пропорції для їх роз’язування, формулюють властивості відношеня і пропорції. Вміють користуватися комп’ютером, створювати презентації та публікаціі.

Очікувані продукти: Комп’ютерна презентація, публікація, реферати.

Девіз проекту: «Математика – це мова, на якій говорять всі точні науки.»

М.І.Лобачевський

Опис проекту

Етапи роботи над проектом:

Визначення теми та мети проекту, його вихідного положення.
Визначення робочої групи
Визначення джерел, способу збору та обробки інформації. Визначення форми проекту. Розподіл обов’язків між членами робочої групи.
Збір та уточнення інформації. Вибір оптимального ходу проекту.
Захист проекту. Оцінка результатів.

Проект передбачає поділ класу на групи, кожна з яких протягом одного – двох тижнів працює над своєю частиною роботи: збирає інформацію, підбирає цікаві факти, готує презентацію зі змістом опрацьованого матеріалу, робить висновки. Керівником проекту виступає вчитель.

Всього формується 4 групи.

Діяльність учнів

Учні одержують завдання об’єднуються в групи.

І група «Історики»

Готують доповідь та презентацію на тему: «Історичні факти про відношення і пропорції». Завданням групи є знайти цікаві історичні факти на дану тему.

ІІ група «Теоретики»

Готують доповідь та презентацію на тему «Властивості і пропорції, їх основна властивість». Завданням даної групи є зібрати інформацію щодо понять відношення і пропорції, виступити з презентацією перед класом. Доступно викладають матеріал, роблять фронтальну перевірку вивченого матеріалу.

ІІІ група «Дослідники»

Досліджують різні види практичних задач, способи їх розв’язання. Займаються пошуком інформації в мережі Інтернет та в наукових посібниках, збирають цікаві дані з теми. Готують доповідь та створюють презентацію.

ІV група «Практики»

Створюються 4 підгрупи: банкіри, географи, кулінари і металурги, які розглядають питання застосування знань про відношення та пропорції до розв’язання задач. Розв’язують поставлені задачі, добирають яскравий та наглядний матеріал, а також створюють презентацію.

Вступ

(Діяльність вчителя)

Математика – цариця наук. Її коханий - істина, її вбрання – простота та ясність. Палац цієї володарки оточений тернистими заростями і, щоб досягти його, кожному треба продертися крізь хащі. Випадковий подорожній не знайде в її палаці нічого привабливого. Краса його відкривається лише розуму, який любить істину і загартовується в боротьбі з труднощами.

Математика створювалася людським розумом упродовж багатьох століть і продовжує розвиватися, а її застосування охоплюють все ширші кола буття.

Математика – велика книга людського досвіду.

На сьогоднішньому уроці ви дізнаєтеся тільки про одну сторінку цієї великої книги. Найкращий спосіб вивчити і запам’ятати – зробити відкриття самому.

Протягом кількох тижнів ми вивчали окремі розділи математики. Це були наші краплинки, які ми сьогодні на уроці зберемо у величезний океан знань про пропорції та відношення. Щоб легше нам було мандрувати по океану пропорції і відношень ми скористаємося маршрутом з відповідними зупинками:

Історики
Теоретики
Дослідники
Практики

Ця подорож допоможе нам вивчити та вдосконалити навички про пропорції та відношення, дізнатися цікаві історичні факти та навчитися розв’язувати задачі про відношення і пропорції, які зустрічаються в повсякденному житті.

(Вчитель повідомляє ціль та задачі проекту, строки здачі проекту, вимоги; учні діляться на групи за інтересами, кожна група отримує завдання, інформуються про те, у якому вигляді здається інформація.)

Історики

Першими відношення та пропорції вивчали давньогрецькі філософи. 2500 років тому у Греції існувала велика філософсько-математична школа, послідовники якої називали себе піфагорійцями. Усе, що робилося в цій школі, ховалося за завісою таємниці та містики. Отримані результати піфагорійці приписували одній і тій самій особі своєму вчителю Піфагору. Кажуть, що не всі послідовники Піфагора мали право бачити свого вчителя. Тому кімната для різних учнів поділялась на дві частини полотняною перегородкою: в одній знаходився Піфагор і його учні, в іншій сиділи ті, хто мав право лише слухати вчителя.
Найулюбленішою галуззю математики у піфагорійців була теорія чисел. Вони вважали, що все на світі підпорядковується тим самим законам, що й відношення цілих чисел. Вони виявили, що струни, відношення довжин яких при однаковому натязі дорівнюють відношенням 2:3, 3:4 і т.д., утворюють при одночасному звучанні акорд, тобто «злиття звуків». Такі ж самі акорди ніби утворюються під час руху Землі, Сонця, Місяця.
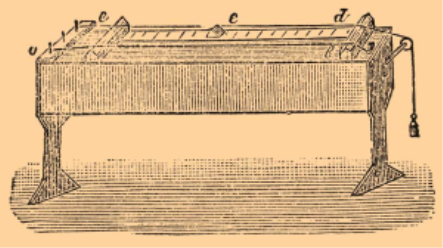
Піфагор був визначним математиком. Але мало хто знає, що він був також і прекрасним музикантом. Він першим здогадався про залежність між струною і мелодією. Для цього він створив однострунний інструмент монохорд і провів багато експериментів. Встановив , що чим довша струна, тим звук нижчий, чим коротша – вищий. А чим товща струна, тим звук нижчий, чим тонша – тим вищий. Але на музичному інструменті не одна, а декілька струн. Щоб усі вони звучали узгоджено, їх довжини повинні перебувати в певному відношенні. Згодом монохорд Піфагора перетворився в домбри, балалайки, гітари, гуслі, бандури, органи, піаніно. За допомогою цих інструментів люди створюють чарівні мелодії, які поліпшують нам настрій. Тепер стає зрозуміло чому вчення про відношення і пропорції древні греки називали музикою.

Теоретики

ВІДНОШЕННЯ

Українська мова багата на синоніми. Наприклад, слова урок і заняття, думати і мислити, вчитель і наставник близькі за значенням.

Подібних прикладів чимало й у математиці: другий степінь числа і його квадрат, один процент, один відсоток і одна сота, промінь і півпряма — вже знайомі тобі «математичні синоніми».

Ось ще один приклад:

частку двох чисел а і b, які не дорівнюють нулю, ще називають відношенням чисел а і b або відношенням числа а до числа b.

Числа а і b називають членами відношення, число а — попереднім членом відношення, а число b — наступним. Наприклад,

16:4 — відношення числа 16 до числа 4;

3:7— відношення числа 3 до числа 7;

Зрозуміло, що відношення двох натуральних чисел а і b можна записати у вигляді дробу . Так само домовились використовувати риску дробу і тоді, коли а і b — дробові числа. Наприклад, відношення 0,3:1,2 записують і так: .

Отже, відношення чисел а і b можна записати двома способами:

або а : b

Найчастіше вибір способу запису визначається його компактністю. Наприклад, запис відношення числа до числа у вигляді не зовсім зручний.

Часто відношення чисел використовують тоді, коли треба порівняти дві 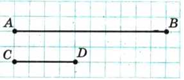величини. На рисунку зображено два відрізки: АВ = 5 см, СD = 2 см. Відношення довжини відрізка АВ до довжини відрізка СD дорівнює 5 : 2 або 2,5. Це відношення показує, що відрізок АВ у 2,5 раза більший за відрізок СD або що відрізок АВ становить відрізка СD.

Відношення довжини відрізка СD до довжини відрізка АВ дорівнює 2:5. Це відношення показує, що довжина відрізка СD становить довжини відрізка АВ.

Отже, відношення чисел а і b показує, у скільки разів число а більше за число b або яку частину число а становить від числа b.

Якщо а і b — натуральні числа, то для відношення «працює» основна властивість дробу:

відношення не зміниться, якщо його члени помножити або поділити на одне й те саме число, яке не дорівнює нулю.

Ця властивість залишається справедливою й тоді, коли члени відношення — дробові числа. Це правило називають основною властивістю відношення.

Наприклад,

;

Ці приклади підказують такий висновок: відношення дробових чисел можна замінити відношенням натуральних чисел.

Часто на практиці використовують відношення величин:

• швидкість — відношення довжини пройденого шляху до часу, за який пройдено цей шлях;

• ціна — відношення вартості товару до кількості одиниць його виміру (кілограмів, літрів, метрів, коробок, пачок, пакетів і т. ін.);

• масштаб карти — відношення відстані на карті до відповідної відстані на реальній місцевості;

• густина — відношення маси речовини до її об’єму;

• продуктивність праці — відношення обсягу виконаної роботи до часу, за який було виконано цю роботу.

Приклад. Знайдіть відношення 3,2 м до 16 см.

Щоб знайти відношення двох величин, треба спочатку виразити їх в однакових одиницях виміру, а потім виконати ділення:

3,2м : 16 см = 320 см : 16 см = 20.

ПРОПОРЦІЇ

Оскільки 3,6 : 0,9 = 4 і 1,2 : 0,3 = 4, то справедливою є рівність 3,6 : 0,9 = 1,2 : 0,3, яку називають пропорцією.

Рівність двох відношень називають пропорцією.

У буквеному вигляді пропорцію можна записати так:

a:b = c:d або .

Наведені записи читають: «відношення а до b дорівнює відношенню с до d або «а відноситься до b, як с відноситься до d».

Числа a i d називають крайніми членами пропорції, а числа b і с — середніми членами пропорції.

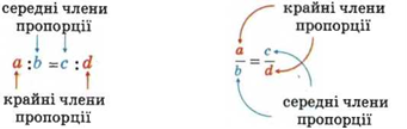
У пропорції 3,6 : 0,9 = 1,2 : 0,3 числа 3,6 і 0,3 — крайні члени, числа 0,9 і 1,2 — середні члени.

Зауважимо, наприклад, що відношення 2:4 і 3 : 9 не рівні, тому утворити пропорцію вони не можуть.

Для пропорції розглянемо добуток крайніх членів 1,5∙4 і добуток середніх членів 2∙3. Вони рівні! Ця властивість притаманна будь-якій пропорції. Вона виражає основну властивість пропорції:

добуток крайніх членів пропорції дорівнює добутку и середніх членів.

Це означає:

якщо , то ad=bc

Правильне і таке твердження:

якщо а, b, с і d — числа, які не дорівнюють нулю, і аd= bс, то відношення рівні й можуть утворити пропорцію .

Наведена властивість дає можливість установлювати рівність двох відношень, не знаходячи їх значень. Наприклад, щоб установити, чи утворюють відношення 0,25: і 1,4 : 40 пропорцію, досить перевірити, чи рівні добутки 0,25∙40 і ∙1,4.

Отримуємо: 0,25∙40 = 10, ∙1,4 = 10. Отже, маємо пропорцію

0,25: = 1,4 : 40.

Також зазначимо, що з рівності аd = bс випливають, наприклад, і такі пропорції: , .

Приклад 1. Знайдіть невідомий член пропорції 9 : x= 3 : 7. Використовуючи основну властивість пропорції, маємо:

З ∙ x = 9 ∙ 7;

Приклад 2. Скільки коштують 3,2 м тканини, якщо за 4,2м цієї тканини заплатили 63 грн.?

Нехай 3,2 м тканини коштують х грн. Запишемо коротку умову задачі в такому вигляді:

3,2м — х грн.;

4,2м — 63 грн.

Відношення і рівні, оскільки кожне з них показує, скільки коштує 1 м даної тканини.

Тоді маємо:

і ;

x=16∙3 = 48

Відповідь: 48 грн.

Фронтальне опитування:

Що називають відношенням двох чисел?

Що називають пропорцією?

Як називають числа, з яких складається пропорція?

Сформулювати основну властивість пропорції.

Дослідники

Насамперед потрібно розрізняти практичні і прикладні задачі. У методиці навчання математики існують різні тлумачення поняття “прикладна спрямованість”.

Ю.М. Налягін і В.В. Пікан розрізняють поняття “прикладна” і “практична” спрямованість.

На їх погляд:

Прикладна спрямованість навчання математики – це орієнтація змісту і методів навчання на застосування математики в техніці і суміжних науках; у професійній діяльності; в народному господарстві і побуті». Згідно з таким тлумаченням міжпредметні зв’язки, політехнічна спрямованість охоплюються поняттям “прикладна спрямованість. Прикладна спрямованість сприяє формуванню наукового світогляду і показує роль математики в сучасному виробництві, економіці, науці.

Практична спрямованість навчання математики – це спрямованість змісту і методів навчання на розв’язування задач і вправ, на формування у школярів навичок самостійної діяльності математичного характеру.

У реальному процесі навчання прикладна і практична спрямованість звичайно функціонують спільно.

Дещо інакше розуміємо прикладну спрямованість В.А. Долінгер. Він вважає, що «прикладна спрямованість математичних знань повинна означати як їх практичне застосування, так і їх теоретичне значення в самій математиці. Лише в цьому випадку буде виховуватися в учнів справжня повага до сили наукових знань».

Прикладна спрямованість навчання математики найбільше реалізується при розв’язування прикладних задач. Під прикладними задачами в школі здебільшого розуміють задачі, які виникають поза курсом математики і розв’язуються математичними методами і способами, які визначаються в шкільному курсі.

Сформулюємо основні вимоги до прикладних задач, які використовуються у навчанні математики.

1.Задачі повинні мати реальний практичний зміст, який забезпечує ілюстрацію практичної цінності і значущості набутих математичних знань.

2. Задачі повинні відповідати шкільним програмам і підручникам за формулюванням і змістом методів і фактів, які будуть використовувати в процесі їх розв’язування.

3. Задачі повинні бути сформульовані доступною і зрозумілою мовою, не містити термінів, з якими учні не зустрічалися і які вимагатимуть додаткових пояснень.

4. Числові дані в прикладних задачах повинні бути реальними, відповідати існуючим в практиці.

5. У змісті задачі по можливості повинен бути відображений особистий досвід учнів, місцевий матеріал, який дозволяє ефективно показати використання математичних знань і викликати в учнів пізнавальний інтерес.

6. Прикладні задачі повинні відображати ситуації промислового і сільськогосподарського виробництва, економіки, торгівлі, ілюструвати застосування математичних знань у конкретних професіях людей.

7. У прикладних задача числові дані, як правило, мають бути наближеними, а при їх розв’язуванні необхідно використовувати обчислювальні засоби, зокрема ЕОМ.

8. При розв’язанні прикладних задач у класах з поглибленим вивченням математики їх формулювання може бути розширене і являти собою деяке теоретичне зведення до проблеми, що вивчається. Сама проблема може мати багатоступеневе розв’язання, при якому кожний наступний етап розвиває і доповнює попередній.

Відношення і пропорції загальновживані у повсякденному житті людини. Наприклад, розрахунок відсоткового відношення величини калорій або працездатного населення регіону; прийняття рішень у сфері фінансових операцій, розрахунок власних та родинних фінансів, комунальних платежів; вміння розпоряджатись власними коштами, в простих ситуаціях оцінювати очікуванні та реальні витрати.

Все це і багато іншого дозволяє нам побачити, що відношення і пропорції використовуються в житті людини і вивчення цієї теми, так як і математики загалом являється необхідною складовою нашого життя.

Практики

1 підгрупа – Банкіри

«Приват Банк» — один з найбільших банківУкраїни. Національна мережа банківського обслуговування Приват Банку включає понад 3 000 філій і відділень на всій території України. Приват Банк є найбільшим оператором ринку роздрібних банківських послуг — за станом на 1 травня 2007 року банк обслуговує 13 млн рахунків фізичних осіб, обсяг залучених банком коштів громадян досяг 16,373 млрд гривень. Приват Банк є найбільшим емітентом і еквайєром платіжних карток в Україні. На сьогодні банком емітовано понад 19,98 мільйона карток, у мережі обслуговування карток працює 7 030 банкоматів і 54 486 POS-терміналів.

Задача

Клієнт Приват Банку поклав на рахунок 60000 грн. Скільки грошей буде у неї на рахунку через рік, якщо банк виплачує 2,5% річних? Розв’язання.

60000грн – 100%

х грн – 2,5%

;

60000грн + 1500грн = 61500грн

Відповідь: 61500 грн.

2 підгрупа Географи

Наша група підготувала пропозиції де провити канікули. Перед вами карта України, незабаром канікули і вас чекають цікаві подорожі. Ми пропонуємо вам такі маршрут:

- до столиці України – Києва;

- до міста Запоріжжя.

На карті є масштаб, ми на уроках географії та математики вчили, як ним користуватися. Заміряйте відстань від нашого міста до вибраного місця подорожі і знайдіть скільки до нього кілометрів, використовуючи знання пропорції.

А наші консультанти, якщо у вас виникне потреба, проінформують вас і допоможуть.

На кожному столі карта України. Учні лінійкою виміряють відстань від міста Миколаїв до місця екскурсії, використовуючи масштаб карти. Складають пропорцію і визначають відстань на місцевості.

Консультанти географи – картографи допомагають і перевіряють.

Задача

Відстань між містом Миколаїв та Київ на карті становить 8,4 см. Яка відстань між цими містами, якщо її масштаб 5000000 (в 1 см 50 км)?

Розв’язання:

1 см – 50 км

8,4 см – х км

;

Відповідь: 420 км між містами Миколаїв так Київ.

Задача

Відстань між містом Миколаїв та Запоріжжя на карті становить 5,4 см. Яка відстань між цими містами, якщо її масштаб 5000000 (в 1 см 50 км)?

Розв’язання:

1 см – 50 км

5,4 см – х км

;

Відповідь: 270 км між містами Миколаїв так Запоріжжя.

3 підгрупа Кулінари

На уроках трудового навчання ми вивчали технологію приготування кулінарних страв. Тут ми побачили що без відношень і пропорцій не обійтись . Тому пропонуємо вам таку задачу.

Задача

З 10 кг. свіжих яблук виходить 8 кг. яблучного пюре. Скільки можна одержати яблучного пюре з 44 кг. свіжих яблук ?

Розв’язання

З 10 кг. яблук – виходить 8 кг. пюре

З 44 кг. яблук – виходить Х кг. пюре

;

Відповідь : з 44 кг яблук виходить 35,2 кг пюре.

підгрупа Металурги

На додаткових уроках ми вивчали сплави різних речовин та їх склад і для нас це виявилося дуже цікавим. Пропонуємо і вам занурити в світ різних речовин та розв’язати задачу

Задача

У 400г сплаву міститься 176г міді. Який відсоток міді у даному сплаві?
Розв’язання.

400 г – 100%

176г – х%

;
Відповідь: 44% міді у даному сплаві.

Висновок

В курсі математики 6 класу відкривається чи не найширше поле для застосування прикладних задач. Досить цікавими можуть бути задачі на визначення відсотку речовини в предметі, банківські розрахунки, визначення раціонального харчування, робота з географічними даними. За період вивчення теми пропорції та відношення ми дізналися масу цікавих та корисних відомостей з цієї теми , тому для закріплення цього матеріалу розгадаємо кросворд.

Питання :