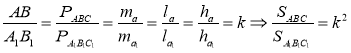Відношення площ подібних трикутників

Тема. Відношення площ подібних трикутників

Мета: домогтися засвоєння учнями змісту та ідеї доведення теоре­ми про відношення площ подібних трикутників. Сформувати вміння відтворювати зміст теореми та застосовувати її під час розв'язування задач.

Тип уроку: засвоєння вмінь та навичок.

Наочність та обладнання: конспект «Відношення площ подібних трикутників».

Хід уроку

І. Організаційний етап

II. Перевірка домашнього завдання

Учитель збирає зошити учнів із виконаною домашньою самостій­ною роботою (див. вище). Учням оголошується правильне розв'язання за рисунками, зображеними на дошці заздалегідь.

Контрольні моменти обговорюються.

III. Формулювання мети і завдань уроку

Учитель пропонує учням відповісти на запитання, зміст яких наштовхне учнів на роздуми відповідно до теми уроку.

1. У паралелограмі проведено діагональ. На які фігури ця діагональ ділить даний паралелограм? Що можна сказати про площі утворе­них фігур? Чому?
2. У паралелограмі проведено дві діагоналі. На які фігури ці діагоналі ділять даний паралелограм? Що можна сказати про площі утворе­них фігур? Чому?
3. У трапеції проведено діагоналі. На які фігури ці діагоналі ділять дану трапецію? Що можна сказати про площі утворених фігур? Чому?

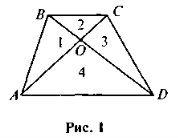Під час пошуку відповідей на останнє запитання (див. рис. 1) учні мають усві­домити, що, на відміну від діагоналей паралелограма, діагоналі трапеції не ділять ЇЇ на трикутники, серед яких є пари рівних. Серед чотирьох здобутих трикутників є два рівновеликих (трикутники 1 і 3), а також два подібних (2 і 4).

Отже, формулюється питання: «Що ми знаємо про площі подібних трикутників?»  Логічно припустити, що відповідь на це питання (тобто встановлення залежності між площами подібних фігур та вираження її у числовій формі, а також формування вмінь застосування цієї залежності під час розв'язування задач), і буде головною метою уроку.

IV. Актуалізація опорних знань

З метою формування свідомого розуміння учнями змісту та доведення теореми про відношення площ подібних трикутників учні мають повторити зміст вивчених раніше понять.

Виконання усних вправ

1. Які два трикутники називаються подібними?
2. Що означає запис: ΔABC подібний до ΔMNK ?
3. Що називають коефіцієнтом подібності трикутників?
4. Нехай у подібних трикутниках ΔАВС  і ΔMNK 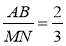. Для яких ще елементів цих трикутників буде виконуватись таке саме відношення?

V. Засвоєння знань

План вивчення нового матеріалу

1. Теорема (про відношення площ подібних трикутників): формулю­вання та доведення.
2. Приклади застосування теореми (про відношення площ подібних трикутників).

Традиційно на завершення вивчення теми «Площі» у 9 класі вивча­лась теорема про відношення площ подібних многокутників, дове­дення якої складалось із двох частин: 1) доведення твердження те­ореми для трикутників; 2) доведення твердження теореми для про­стих многокутників через доведене твердження для трикутників. За новою програмою у 8 класі вивчається тільки теорема про відно­шення площ подібних трикутників (тобто особливий випадок тео­реми про площі подібних многокутників). Це обумовлено тим, що поняття подібності многокутників не вивчалось.

Доведення теореми майже повністю відповідає традиційному доведенню властивості площ подібних трикутників і спирається на властивість сторін подібних трикутників, на ознаки подібності прямокутних трикутників та застосування формули площі трикутника (доведення можна провести простіше, якщо використати властивості відношень відповідних лінійних елементів подібних трикутників, сформульовані і доведені в темі «Подібність трикутників»). Після виконання роботи з повторення змісту цих понять (див. усні вправи) доведення теореми має бути зрозумілим усім учням.

Як приклад із застосування теореми про відношення площ подібних трикутників можна розглянути з учнями опорний факт, який є узагальненням задачі, а саме: площа трикутника, що відтинається від даного його середньою лінією, дорівнює чверті площі даного Трикутника. Розуміння твердження теореми та наслідку відбувається під час розв'язування усних вправ та завдань за готовими рисунками.

VI. Формування первинних умінь

Виконання усних вправ

1. Визначте, як зміниться площа трикутника, якщо кожну його сто­рону:

а) збільшити в 4 рази;

б) зменшити в 3 рази;

в) зменшити в п разів.

2. Визначте, як треба змінити кожну сторону трикутника, щоб його площа:

а) зменшилася в 25 разів;

б) збільшилася в 49 разів;

в) збільшилася в  п² разів.

3. Відношення площ двох трикутників дорівнює 4. Чи означає це, що дані трикутники подібні з коефіцієнтом 2?
4. В одного із двох правильних трикутників висота удвічі менша, ніж у другого. У скільки разів площа другого трикутника більша за пло­щу першого? У скільки разів периметр другого трикутника біль­ший, ніж периметр першою?
5. Висота одного правильного трикутника дорівнює стороні другого. Яке відношення площ цих трикутників?
6. Площі двох подібних трикутників відносяться як 1 : 16. Як відно­сяться: а) відповідні висоти; б) периметри; в) відповідні кути цих трикутників?
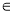7. Площа ΔАВС дорівнює 48 см². Через середину висоти BD прове­дено пряму MN, паралельну АС. Чому дорівнює площа трикут­ника MBN (М АВ, N BC)?

Виконання письмових вправ

1. Відомо, що ΔАВС ~ ΔА₁В₁С₁, причому 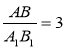. Знайдіть:

a) S_AВC, якщо см²;

б) , якщо S_AВC  = 9 см².

2. Відомо, що ΔABC ~ Δ А₁В₁С₁. Знайдіть:

а) сторону А₁В₁, якщо S_AВC = 24 см², = 6 см², АВ = 8 см;

б) площу  трикутника АВС, якщо ВС = 2 см, В₁С₁ = 6 см, =18 см².

3. Катети прямокутного трикутника дорівнюють 6 см і 8 см. Знайдіть площу трикутника, утвореного середніми лініями цього трикутника.
4. Два трикутники подібні з коефіцієнтом 3, причому площа одного з них на 24 см² більша за площу іншого. Знайдіть площі цих три­кутників.
5. Площі двох подібних трикутників дорівнюють 75 м² і 300 м². Пери­метр першого трикутника дорівнює 54 м. Знайдіть периметр друго­го трикутника.
6. На плані земельна ділянка має форму трикутника з площею 2,5 см². Знайдіть площу ділянки, якщо масштаб плану 1 : 1 000.

 Розв'язування запланованих задач сприяє закріпленню в учнів фор­мулювання теореми та розуміння, що з доведеного в підручнику твердження випливають два різних варіанти його застосування:

• Якщо трикутники подібні з коефіцієнтом подібності k (від­ношенням відповідних сторін, висот, медіан, периметрів, тобто відношенням відповідних лінійних елементів), то відношення їх площ дорівнює k².
• Якщо трикутники подібні і відношення площ дорівнює k², то коефіцієнт подібності (відношення відповідних сторін, висот, медіан, периметрів, тобто відношення відповідних лінійних елементів) дорівнює k.

VII. Підсумки уроку

Відповідні сторони двох подібних трикутників дорівнюють а і b . Заповніть пропуски так, щоб рівності стали правильними (рис. 2).

; ; ; ; ;

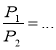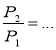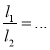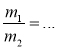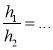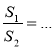
(l, т, h — відповідні бісектриси, медіани і ви­соти трикутників).

VIII. Домашнє завдання

Вивчити   зміст   та   доведення   теореми   про відношення площ подібних трикутників.

Розв'язати задачі.

1. Сторони рівносторонніх трикутників дорівнюють 2 см і 6 см. Знай­діть відношення їх площ.
2. Знайдіть площу трикутника, якщо трикутник, утворений середні­ми лініями даного трикутника, має площу 5 см².
3. Відповідні сторони двох подібних трикутників відносяться як 2 : 3. Площа другого трикутника дорівнює 81 см². Знайдіть площу пер­шого трикутника.

Розв'язати задачі на повторення.

1. Сторони прямокутника відносяться як 5 : 12. Знайдіть площу прямокутника, якщо його діагональ дорівнює 26 см.
2. На діагоналі квадрата як на стороні побудовано інший квадрат. До­ведіть, що його площа вдвічі більша за площу даного квадрата.
3. Висоти паралелограма дорівнюють 12 см і 16 см, а кут між ними — 30°. Знайдіть площу паралелограма.