Синус, косинус і тангенс гострого кута прямокутного трикутника

Тема. Синус, косинус і тангенс гострого кута прямокутного трикутника

Мета: домогтися засвоєння учнями змісту означень синуса, коси­нуса, тангенса і котангенса гострого кута прямокутного трикутника та їх властивостей, що випливають із теореми Піфагора, подібності пря­мокутних трикутників та властивостей сторін прямокутного трикутни­ка (проти більшої сторони лежить більший кут, і навпаки). Сформува­ти вміння відтворювати зміст означень та їх властивостей, а також зна­ходити значення тригонометричних функцій гострого кута за даними прямокутного трикутника.

Тип уроку: засвоєння нових знань.

Наочність та обладнання: конспект «Означення тригонометричних функцій гострого кута».

Хід уроку

І. Організаційний етап

Як завжди, на початку вивчення нового розділу слід надати учням інформацію:

• про орієнтовний план вивчення розділу;
• кількість навчальних годин;
• приблизний зміст матеріалу;
• основні вимоги до знань та вмінь учнів;
• приблизний зміст завдань, що будуть винесені на контроль.

(Цю інформацію можна помістити на стенді «Довідково-інформаційний куточок» у кабінеті математики та з метою економії часу запропонувати учням для самостійного ознайомлення в позаурочний час).

II. Перевірка домашнього завдання

Якщо вдома учні виконували письмове завдання (аналіз розв'язання задач контрольної роботи або корекційну роботу тощо), то правиль­ність виконання цієї роботи вчитель перевіряє, зібравши зошити уч­нів на перевірку.

III. Формулювання мети і завдань уроку

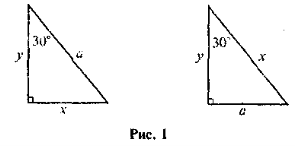Щоб сформулювати мету уроку, достатньо слів учителя про те, що в науці і техніці часто розв'язують задачі, в яких за відомими стороною і кутом прямокутного трикутника треба знайти невідомі його сторони і кути, або навпаки, знаючи сторони прямокутного трикутник, обчис­лити його кути. Прикладом таких задач є добре відомі задачі на засто­сування співвідношень між катетом, що лежить проти кута 30°, і гіпо­тенузою, рисунки до яких подані нижче (див. рис. 1).

Знайдіть х, у, якщо а — відоме.

Розв'язання цих задач демонструє залежність між довжиною катета, протилежним кутом 30° і довжиною гіпотенузи, тобто залежність між сторонами прямокутного трикутника та його кутом. Міркуючи послідовно, можна передбачити існування загальних залежностей між сторонами і кутами прямокутного трикутника, які. можуть бути записані в алгебраїчному вигляді і одним з окремих випадків яких є відоме співвідношення між довжиною катета, протилежним кутом 30° і довжиною гіпотенузи. Отже, мета уроку визначається як необхідність вивчення співвідношень між сторонами і кутами прямокутного трикутника та вивчення їх властивостей, а також опанування способів застосування цих співвідношень під час розв'язування задач.

IV. Актуалізація опорних знань

З метою формування свідомого розуміння учнями змісту означень відношень між сторонами і кутами прямокутного трикутника та їх властивостей учні мають повторити зміст означення прямокутного трикутника та його елементів (поняття катета, що лежить проти даного гострого кута, та катета, що прилеглий доданого кута), ознак подібності прямокутних трикутників та властивості сторін подібних трикутників.

Повторення цього матеріалу можна провести у формі бесіди або під час виконання усних вправ.

Виконання усних вправ

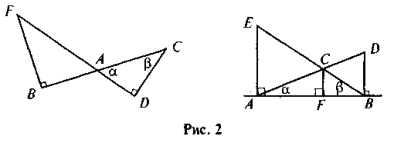
На рис. 2 знайдіть усі пари подібних прямокутних трикутників і доведіть їх подібність. У кожному трикутнику назвіть найменший катет та кут, що лежить проти цього катета, а також кут, що є прилеглим до цього катета.

V. Засвоєння знань

План вивчення нового матеріалу

1. Означення синуса гострого кута прямокутного трикутника. Його позначення.
2. Означення косинуса гострого кута прямокутного трикутника. Його позначення.
3. Означення тангенса гострого куга прямокутного трикутника. Його позначення.
4. Означення котангенса гострого кута прямокутного трикутника. Його позначення.
5. Властивості тригонометричних функцій гострого кута прямокут­ного трикутника.

 Вивчення співвідношень між сторонами і кутами в прямокутно­му трикутнику традиційно розпочинається з уведення понять си­нуса, косинуса, тангенса і котангенса гострого кута прямокутного трикутника та формулювання і доведення їх властивостей (залеж­ність числових значень тільки від міри кута). У цьому плані теоре­тичний матеріал нового підручника не відрізняється від традицій­ного змісту відповідного розділу попереднього підручника. Проте, у зв'язку зі зміною послідовності вивчення матеріалу за новою програмою порівняно з попередньою, обґрунтування властивостей си­нуса, косинуса, тангенса і котангенса гострого кута прямокутного трикутника змінилося. Тепер сформульовані властивості дуже лег­ко доводяться із посиланням на подібність прямокутних трикут­ників (трикутники із спільним гострим кутом подібні за ознакою, отже, їх відповідні сторони пропорційні за означенням подібності трикутників).

Слід відзначити, що в новому підручнику міститься додатковий матеріал щодо семантики понять «синус», «косинус», «тангенс»; цей матеріал може допомогти учням швидше запам'ятати зміст означень цих понять.

Серед властивостей, які використовуються в задачах і які слід побачити «між рядками», необхідно виділити властивість, яка вип­ливає з того, що в трикутнику проти більшого кута лежить більша сторона, і навпаки. Ця властивість — зростання синуса го­строго кута за зростання кута і спадання косинуса гострого кута за зростання кута — на цьому етапі вивчення тригонометрії може бути сформульована у вигляді твердження: більшому гострому куту прямокутного трикутника відповідає більше значення синуса і менше значення косинуса. Вивчення змісту теоретичного матеріалу уроку доречно проводити відповідно до підручника за планом, по­даним вище. Під час вивчення питання про спосіб позначення три­гонометричних функцій слід одразу, попереджаючи типові помил­ки учнів, пояснити, що ці позначення є скороченим записом від­повідної назви латинськими літерами (наприклад, sin α — це ско­рочення виразу «синус кута альфа»), а не добуток. Крім того, ос­кільки не існує абстрактних понять синуса, косинуса, тангенса і котангенса (ці поняття обов'язково асоціюються з певним гострим кутом прямокутного трикутника), то й записи типу sin, cos тощо просто не мають змісту.

Домогтися розуміння учнями змісту вивченого матеріалу та його закріплення можна шляхом виконання вправ (див. нижче), запропо­нованих учням під час вивчення нового матеріалу.

1. Один з учнів 8 класу накреслив на дошці прямокутний трикутник із катетами 30 см і 50 см та обчислив значення синуса, косинуса, тангенса і котангенса гострого кута, що лежить проти меншого ка­тета. Потім до дошки вийшов інший учень і сказав, що накреслить прямокутний трикутник із катетами 45 см і 75 см, у якому синус, косинус, тангенс і котангенс гострого кута, протилежного до най­меншого катета, будуть більшими, бо його трикутник більший. Чи не помиляється цей восьмикласним? У чому його помилка?
2. Які з чисел:

1; 0,5; ; ; ; ; 0; -0,3 можуть бути числовими значеннями синуса, косинуса, тангенса і котангенса гострого кута прямокутного трикутника? Поясніть.

3. Прочитайте записи: sin A = 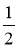; соs B = 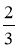; tg γ = 1; ctg φ = 2. Пояс­ніть, що вони означають.

Після обговорення питань слід провести узагальнення способів застосування вивченого матеріалу, якщо треба знайти значення синуса, косинуса, тангенса і котангенса гострого кута прямокутного трикутника, то використовують означення цих понять; якщо ж треба відповісти на питання стосовно даних значень тригонометричних функцій, то слід використовувати їх властивості. У вивченні нового матеріалу користуємося конспектом.

VI. Формування первинних умінь

Виконання усних вправ

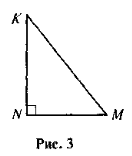
1. За рисунком 3 визначте, яка тригонометрична функція кута К ви­ражається відношенням:

а) ;    б) ;    в) .

2. У прямокутному трикутнику KMN (рис. 3) KN > MN. Який із гострих кутів трикутника має більший синус; більший косинус; більший тангенс?
3. Чи може синус гострого кута прямокутного трикутника дорівнювати 0,99; 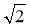, 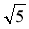– 2?
4. Чи може добуток синуса і косинуса одного кута дорівнювати одиниці? А добуток танген­са і котангенса?
5. Чи може тангенс гострого кута прямокутного трикутника дорівню­вати 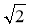; 0,01; 100?

Виконання письмових вправ

1. Накресліть за допомогою транспортира прямокутний трикутник із гострим кутом 40°. Виміряйте його сторони та обчисліть синус, ко­синус і тангенс цього кута.
2. Побудуйте прямокутний трикутник ЛИС, в якому:

а) tg А = ;  б) sin А = .

3. Побудуйте кут 75°. За допомогою додаткових побудов і вимірювань знайдіть синус, косинус, тангенс і котангенс цього кута.
4. Побудуйте гострий кут ос, якщо:

a) sin α = ; б) cos α = .

5. Доведіть, що для будь-якого гострого кута A tg A > sin A.
6. Катеті гіпотенуза прямокутного трикутника відповідно дорівню­ють 6 см і 10 см. Знайдіть:

а) синус гострого кута, що лежить проти більшого катета;

б) косинус гострого кута, прилеглого до меншого катета;

в) тангенс гострого кута, що лежить проти більшого катета.

 Виконання всіх вправ має на меті закріплення учнями вивченої термінології та вивчених властивостей, а також розуміння сфери застосування вивченого матеріалу (див. висновок попереднього етапу уроку). Розв'язання задач передбачає додаткове повторення теореми Піфагора для обчислення невідомої сторони прямокутно­го трикутника перед застосуванням вивчених означень.

VII. Підсумки уроку

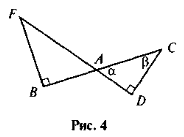
Подайте різними способами косинус, синус і тангенс кутів α і β (рис. 4).

VIII. Домашнє завдання

Вивчити зміст означень синуса, косинуса, тангенса гострого кута, прямо­кутного трикутника та доведення їх власти­востей.

Розв'язати задачі.

1. Накресліть гострий кут. Позначте на одній стороні кута дві точки і проведіть із них перпендикуляри до іншої сторони кута.

а) Виміряйте сторони прямокутних трикутників, що утворилися, та обчисліть двома способами синус побудованого кута. Порівняйте
результати.

б) Обчисліть косинус побудованого кута двома способами — за означенням і за основною тригонометричною тотожністю. Порівняйте результати.

2. Катети прямокутного трикутника дорівнюють 8 см і 15 см. Обчис­літь синус, косинус і тангенс найменшого кута трикутника.
3. Висота рівнобедреного трикутник, проведена до основи, дорівнює 5 см, а довжина основи — 24 см. Знайдіть синус, косинус, тангенс і котангенс кута при основі трикутника.
4. Доведіть, що для будь-якого гострого кута A cos A < ctg А.