Відсоткові розрахунки

Відношення і пропорції. Відсоткові розрахунки.

Відношення і пропорції

 Частка від ділення двох дійсних чисел називається відношенням. Вона показує, у скільки разів одне число більше від другого, або яку частину одне число становить від другого. Рівність двох відношень називають пропорцією: а:b=c:d або .

Основна властивість пропорції: добуток крайніх членів дорівнює добутку середніх: ad=bc

Дві взаємно залежні величини називаються пропорційними, якщо відношення їх значень залишається сталим. Стале відношення пропорційних величин називається коефіцієнтом пропорційності. Він показує скільки одиниць однієї величини припадає на одиницю іншої.

Прямопропорційні величини – зі збільшенням (зменшенням) однієї з пропорційних величин у кілька разів інша величина збільшується (зменшується) у стільки ж разів. Наприклад, час роботи і заробіток, одержаний за цей час при поденній оплаті праці. Властивість прямої пропорційності: відношення двох довільно взятих значень першої величини дорівнює відношенню двох відповідних значень другої величини. Оберненопропорційні величини – зі збільшенням (зменшенням) однієї з пропорційних величин у кілька разів інша величина зменшується (збільшується) у стільки ж разів. Наприклад, зі збільшенням швидкості у кілька разів час пересування зменшується у стільки ж разів. Властивість оберненої пропорційності: відношення двох відношення двох довільно взятих значень однієї величини дорівнює оберненому відношенню відповідних значень другої величини.

• Задача 1. У басейн за 7 хв. вливається 116л води. Скільки води вливається за 15 хв.?
• Задача 2. 9 тракторів зорюють поле за 8 год. За який час зорюють це поле 4 трактори?
• Завдання. Із формули 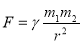виразити кожну зі змінних.

Відсоткові розрахунки

Відсоток – це частина від цілого.

Щоби перетворити дане число на відсотки, треба це число помножити на 100.

Наприклад,

а) 0,245=(0,245*100)%=24,5%    б)  в)

Щоби перетворити дане число відсотків на дріб чи ціле число, треба поділити дане число відсотків на 100.

Наприклад,

а) 52%=, б) , в) 250%=.

Основні задачі на відсотки

1. Знаходження відсотків від числа: .

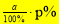Щоби знайти відсотки від числа, треба ці відсотки записати звичайним чи десятковим дробом і помножити дане число на здобутий дріб.

• Задача 3. Знайти 17% від числа 400.
• Задача 4. На ціну товару зроблено послідовно знижки на 15%, а потім на 8%. На скільки відсотків знизилася ціна товару?
• Задача 5. Місячна зарплата робітника становить 2400 грн. Додатково було нараховано премію 24% від місячної зарплати. Скільки гривень становить премія?

2. Знаходження числа за відомими його відсотками: .

Щоби знайти число за його відсотками, треба відсотки записати звичайним чи десятковим дробом і поділити дане число на здобутий дріб.

• Задача 6. Знайти число 15% якого дорівнює 90.
• Задача 7. При перемелюванні пшениці вихід борошна становить 80%. Скільки пшениці треба змолоти, щоб отримати 520 кг борошна?
• Задача 8. З овочевого складу відправлено 33,6% усієї кількості картоплі. На складі залишилося 33,2 т картоплі. Скільки тон картоплі було на складі спочатку?

3. Знаходження відсоткового відношення двох чисел: .

Щоби знайти відсоткове відношення двох чисел, треба знайти їх відношення і виразити його у відсотках.

Задачі такого типу розв’язують при визначенні відсотків успішності, відвідування, жирності молока, вологості, сушіння. Тут відношення двох чисел показує, яку частину становить перше число від другого (за основне беруть те, з яким порівнюють число).

• Задача 9. З чотирьох запланованих деталей токар виточив три. На скільки відсотків він виконав план?
• Задача 10. Завдяки раціональному розкрою металевого листа робітник вирізав 35 деталей замість 20. Скільки відсотків економії металу досягається при цьому?
• Задача 11. Книга коштувала 38 грн. Якою буде ціна книги після послідовних підвищень її на 20% і 25%?
• Задача 12. До просушування вологість зерна становила 23%, а після просушування – 12%. На скільки відсотків зменшилася маса зерна після просушування?

Наприклад, збільшення числа на 50% – це збільшення його у 1,5 рази, оскільки 150%=150/100=1,5;

 збільшення числа а на 30% = а+а*0,3=1,3а. Тобто число а збільшилося у 1,3 рази;

 зменшення числа в 1,2 рази: 1,2=, тому число становитиме свого попереднього значення;

 якщо після зменшення нове число становить свого попереднього значення, то воно зменшилося в рази.