Відсоткові відношення і пропорційний поділ. Збірник задач

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Збірка задач професійної спрямованості

з математики

 

«Відсоткове відношення і пропорційний поділ

 в житті людей»

 

Автор: Сліпович Н.М.,

вчитель математики

 

 

 

 

 

 

 

 

 

Синельникове

 

 

 

 

Сліпович Н.М.

«Відсоткове відношення і пропорційний поділ  в житті людей». Збірка задач професійної спрямованості, 2010/  20 с.

 

Відсотки в нашому житті займають значне місце. Різні сфери діяльності, різні технологічні процеси часто вимагають нас виконувати відсоткові розрахунки. Дані задачі показують застосування даних розрахунків у галузях хімічної промисловості, металургії, харчової промисловості тощо.

В даній збірці зібрані задачі за такими темами:

1. Відсотки. Знаходження відсотків від числа

2. Знаходження числа за його відсотками

3. Знаходження відсоткового відношення двох чисел

4. Пропорційний поділ числа на частини

Рекомендується для використання на уроках математики в 5-9 класах.

 

 

 

 

 

 

 

 

 

 

1. Розчин містить 18 % солі. Скільки грамів солі міститься в 340 г цього розчину?

Розв’язання:

Весь розчин -340 г  - 100%, тоді х г солі це 18%. Складаємо пропорцію:

340 г – 100%;

    х г -  18%.

340∙0,18=61,2 (г)

Відповідь: 61,2 г солі.

 

2. Руда містить 70% заліза, Скільки треба взяти руди, щоб отримати 42 т заліза?

Розв’язання:

Вся руда –х кг – 100%,

Вміст заліза  - 42 т – 70 %.

Складаємо пропорцію:

х кг – 100%,

42 т – 70%

х= 42∙100: 70=600(кг)

Відповідь: 600 кг руди.

 

3. При сушіння яблука втрачають 84% своєї ваги. Скільки треба взяти свіжих яблук, щоб одержати 12 кг  сушених?

Розв’язання:

При сушіння залишається тверда маса. 100%-84%=16%.

16% - 12 кг,

100% - х кг.

х= 12∙100:16=75 (кг)

Відповідь: 75 кг свіжих яблук.

 

4. Мідна руда містить 8% міді. Скільки тонн міді міститься в 260 т такої руди?

Розв’язання:

Мідна руда – 260 т – 100%,  мідь  х т -8%. Складаємо пропорцію:

260 т – 100%,

 х т     - 8 %.

х = 260∙8:100= 20,8 (т)

Відповідь: 20,8 т міді.

 

5. Сплав складається з 5 частин міді та 8 частин цинку. Скільки потрібно взяти кілограмів цинку, щоб одержати 520 кг сплаву?

Розв’язання:

Весь сплав складається з 13 рівних частин. Маса сплаву 520 кг. Знайдемо скільки приходиться кг на одну частину.

1. 520: (5+8)=40 (кг) – маса однієї частини.
2. 8∙40=320(кг) – маса цинку

Відповідь: 320 кг цинку.

 

6. Щоб замісити тісто, необхідно взяти борошно, молоко, і олію у відношенні: 8:5:1. Скільки грамів борошна потрібно взяти, щоб вийшло 840 г тіста?

Розв’язання:

І спосіб.

1. 8+5+1=14 (частин) – становить усе тісто.
2. 840: 14= 60(г) – припадає на одну частину.
3. 60∙8=480(г) – потрібно взяти борошна.

ІІ спосіб

Нехай одна частина становить х г. Тоді борошна треба взяти 8х г, молока – 5х г, олії – х г.

Маємо,

8х+5х+х=840;

14х=840;

х=60.

Отже, борошна потрібно взяти 8∙60=480(г)

Відповідь: 480 г.

 

7. Для виготовлення сплаву із міді і цинку взяли мідь і цинк у відношенні 5:3. Скільки взяли кілограмів міді, якщо її було на 12 кг більше ніж цинку?

Розв’язання:

Сплав містить 5 частин міді і 3 таких самих частин цинку. Нехай маса однієї такої частини х кг. Тоді міді взяли 5х  кг, а цинку – 3х кг.

5х-3х=12;

2х=12;

х=6 (кг) – містить одна частина.

5∙6=30 (кг) – вміст міді.

Відповідь: 30 кг

 

Задачі для самостійного розв’язку.

 

1.                Для виготовлення соку беруть 12 частин ягід і 17 частин води. Скільки ягід їм потрібно взяти, щоб отримати 232 кг соку?

Відповідь:  96 кг.

2. Для виготовлення царської корони  використовували сплав, що містить 7 частин золота і 5 частин платини. Скільки кожного металу потрібно взяти, щоб маса корони дорівнювала 2 кг 460 г? Відповідь: 1 кг 435 г золота, 1кг 25 г платини.
3. Сплав містить 6 частин цинку і 8 частин заліза. Скільки потрібно взяти заліза, щоб отримати 448 кг сплаву? Відповідь: 256 кг.
4. Деталь містить 28% міді, 56% заліза, а решта 144 г – нікель Скільки грамів важить деталь?  Відповідь: 900 г.
5. Морська вода містить 6% солі. Скільки води потрібно взяти, щоб отримати 42 кг солі? Відповідь: 700 кг.
6. Під час сушіння гриби втрачають 92% своєї ваги. Скільки свіжих грибів потрібно взяти, щоб отримати 6 кг сушених? Відповідь:75 кг.
7. В насінні сої міститься 20% масла. Скільки масла в 700 кг сої?

         8. З хлопка-сирцю отримали 24 % волокна. Скільки треба взяти   

хлопка-сирцю, щоб отримати480 кг волокна?

 9. Треба обробити ділянку поля 500 га. В перший день обробили    150   га. Скільки відсотків складає оброблена ділянка по відношенню до  всього поля?

         10. Робітник виготовив за зміну 45 деталей замість 36 за планом.   

Скільки процентів фактична вироботка складає по відношенню до  планової?

ІІ розділ

  1. Населення міста за два роки збільшилось з 20 000 до 22 050 людей.  Знайдіть середній щорічний процент приросту населення цього міста.

Розв'язок:

Нехай Х – середній щорічний  процент росту населення.

(20 000 х 0,01 х Х) людей– прирост населення за перший рік.

(20 000 + 200 х Х) людей – кількість населення через рік.

(0,01 х Х х (20 000 + 200 х Х)) людей – прирост населення за другий рік.

20 000 + 200 х Х + 0,01 х Х х (20 000 + 200 х Х)людей– ккількість населення через два роки, а за умовою задачі воно дорівнює 22 050 людей.

 Складаємо і розв’язуємо рівняння: 

20 000 +200 х Х + 0,01 х Х х (20 000 + 200 х Х) = 22 050, Х > 0.

 В результаті отримуємо Х = 5.

Відповідь: 5 %

2. Вода при замерзанні збільшується  на 1/9 свого об’єму . На скільки відсотків свого об’єму збільшиться лід при перетворенні у воду?

Розв’язок:

Якщо V – об'єм води, то (1 + 1/9) х V = 10/9 х V – об’єм  льда.

 

                                         об'єм льда – об'єм  води

шуканий розв’язок =     ________________________  х 100 %;

                                                     об'єм льда

Підставив необхідні величини, отримуємо, що об’єм льда збільшиться на 10%..

Відповідь: на 10%.

3. Якщо першу цифру двозначного числа збільшити на 25%, то отримуємо його другу цифру, а якщо його другу цифру зменшити на 20%. То отримуємо його першу цифру. Знайдіть це двозначне число.

Розв’язок:

Нехай а – перша цифра двузначного числа;

            b – друга цифра двузначного числа.

Маємо систему рівнянь:

1,25a = b;

0,8b = a,

враховуємо, що а, b – цифри, отримуємо, що а = 4 і b = 5.

Відповідь: Шукане двузначне число – 45.

 

4. Банк обіцяв своїм клієнтам річний прирост вкладу 30%. Яку суму може отримати клієнт, якщо покладе в цей банк 450 000 гривень?

Розв’язок:

 1) 4500 * 0,3 = 1350(руб.) – «прирост» за рік.

 2) 4500 + 1350 = 5850(руб.)

 Відповідь: в кінці року на рахунку буде знаходитись 5851 гривень.

 

5. Яку суму треба покласти в банк. Що виплачує 25% річних, щоб в кінці року отримати 1000грн.?

Розв’язок:

1)100% + 25% = 125% - складає 1000 грн. от первинного вкладу.

2)125% = 1,25 = 800 (грн.) – сума вкладу.

Відповідь: сума вкладу 800 грн.

6. В 200 г води розчинили 50 г солі. Яка концентрація отриманого розчину?

Розв’язок:

Концентрація розчину – це процент, який складає маса речовини від маси розчину. Тому потрібно обчислити процент, який складає 50 г солі всієї маси розчину:

1)50 + 200 = 250 (г.) – маса отриманого розчину.

2)(50 / 250) * 100 = 50 * 100 / 250 = 20 (%).

Відповідь: концентрація розчину дорівнює 20%.

7. Протягом січня ціна на яблука виросла на 30%., а у лютому лютому – на 20%. На скільки відсотків піднялась ціна за два місяці?

Розв’язок:

Позначимо первинну ціну  S. В кінці січня вона стала дорівнювати 1.3S, а в кінці лютого 1,2 * (1,3S) = 1,56S. Значить,вона ззросла на 56%.

Розв’язок можна записати так:

Нехай S – первинна  ціна.

1)1,3S – ціна в кінці січня (130% от S).

2)1,2 * (1,3S) = 1,56S – ціна в кінці лютого (120% от 1,3S).

3)1,56S складає 156% от S. 

    156% - 100% = 56%

Відповідь: за два місяці ціна виросла на 56%.

8. Статистика показує, що об’єм знань, накопичених людством, подвоюється кожні 5 років. На скільки відсотків збільшиться запас знань за 1 місяць, за 1 рік, за 10 років?

Розв’язання:

Нехай  Х – об’єм  знань на якийсь рік. Тоді через 5 років знань буде Х*5. Або 500%.

Один місяц = 1/12 року. В 5 роках 5*12=60 місяців, один буде 1/60.

Якщо накопичення знань за 5 років вважати лінійним, то буде так: х*5*1/60=X/12 - стільки знань за місяць. В процентах = x/12*100%

За рік буде X*5*1/5=1X или 100% За 10 років буде (X*5)*5 = X*25 або 2500%.

 

9. Мама дала Павлу гроші на 30 олівців. Виявилось, що в магазині олівцева фабрика проводить рекламну акцію: в обмін на чек про покупку набору з 20 олівців повертає 25% вартості набору. А в обмін на чек про покупку з 5 олівців 10%. Яку най більшу кількість олівців може купити Павло?

Розв’язання:

Треба відмітити, що 25% від вартості 20 олівців – це вартість 5 олівців, а 10% від вартості 5 олівців – це половина вартості олівця.

Зрозуміло, що для отримання максимальної скидки Павло повинен діяти так:

Якщо вистачає коштів, купувати набір з 20 олівців і зразу обмінювати його на чек при виході. Якщо грошей не вистачає, але вистачає на 5, купувати набір з 5 олівців і обмінювати чеки на виході.

Поступаючи таким чином, Павло спочатку купує коробку з 20 олівців і отримує чек на 5 олівців. Після цього у нього буде грошей на 15 олівців. Потім він купує три набори по 5 олівців і отримує на виході вартість одного. Всього виходить 36 олівців.

Відповідь: 36 олівців.

10. Остап Бендер і Кіса Ворб'янінов поділили між собою виручку від продажу слонів населенню. Остап подумав: якщо б я взяв  грошей на 40% більше, то доля Кіси зменшилась б на 60%. Як би змінилась доля Кіси . якби Остап взяв грошей на 50% більше?

Розв’язання:

Нехай Остап взяв собі х рублів, а Кіса – у рублів, тоді за умовою, 0,4х=0,6у. Звідси отримуємо 0,5х=0,75у. Значить, якщо би доля Остапа збільшилась на 50%. То доля Кіси зменшилась на 75%.

Відповідь: зменшилась на 75 %

 

11. Під який відсоток вигідніше покласти гроші в банк на рік: 6 % в рік або ½ відсотків в місяць?

Розв’язання:

Нехай банк начисляє ½ % кожен місяць.Якби ½ % нараховувалась виходячи з суми покладеної на початок року. То в кінці року сума збільшилась на 6%. Проте, починаючи з другого місяця1/2 буде нараховуватися на суму, яка є на рахунку на початок місяця.Тому в кінці року сума окажеться більшою, якщо кожен місяць буде нараховуватися ½ %, ніж 6% річних.

Відповідь: вигідніше другий варіант.

 

12. Екологи запротестували проти великого об’єму лісозаготівель. Голова лісопромхозу заспокоїв їх наступним чином: «В лісі 99% сосен Будуть вирубуватися тільки сосні, після вирубок відсоток сосен залишиться незмінним – 98%». Яка частина лісу відведена для вирубки?

Підсказка

Кількість "не сосен" залишається постійним, а доля "не сосен" збільшується с одного процента до двух...

Розв’язання:

Позначимо через х число дерев, що не є соснами. Тоді до вирубки х складає 100%-99%=1%. А після вирубки х складає 100%-98%=2% лісу. Таким чином до вирубки в лісі було 100х. а після вирубки повинно залишитися 50х дерев. тобто в два рази  менше.

Відповідь: половина

13. Токар виготовляє за 1 год 40 деталей. Замінивши різець на інший з більш міцної сталі, він став виготовляти на 10 деталей в годину більше. На скільки відсотків збільшилась продуктивність праці?

Розв’язання:

Треба дізнатися скільки відсотків складає 10 деталей від 40.

40 деталей – 100%

10 деталей – х%

х=10:40∙100=25%

Відповідь: на 25%.

 

14. Якщо молодий чоловік викурює в день пачку сигарет за ціною 10 грн. Який відсоток свого місячного заробітку витрачає він на сигарети за умови, що заробляє 2000 грн. на місяць і в місяці 30 днів?

Розв’язання:

1)      10 · 30 = 300 (грн.) – витрачає в місяць на сигарети

2)      300 : 2000 = 0,15 (ч.) – витрачає на сигарети

3)      0,15 · 100% = 15 %.

Відповідь: 15%.

 

ІІІ розділ

1. Скільки грамів 4-відсоткового і скільки грамів 10-відсоткового розчинів солі треба взяти, щоб отримати 180 г 6-відсоткового розчину?

Розв’язання:

Нехай треба взяти х г 4-відсоткового розчину і у г 10-відсоткового розчину. Тоді загальна кількість розчину складає х+у=180 (г)

В х г 4-відсоткового розчину  міститься 0,04 х г солі, а в у г 10-відсоткового розчину  - 0,10у г солі, за умовою сумарна кількість повинна складати 6%  від 180 г , тобто 180∙0,06 =10,8 (г) Тому, 0,04х+0,1у=10,8. Отримуємо систему:

х+у=180,                  х+у=180,          2х+2у=360;     3у=180,      х=120                           0,04х+0,1у=10,8;    2х+5у=540;       2х+5у=540;     х+у=180;    у=60     

 

Відповідь: 60 г, 120 г.

 

2. Після того, як змішали 60-відсотковий і 30-відсотковий розчини кислоти, отримали 600г 40-відсоткового  розчину. Скільки грамів кожного розчину змішали?

Розв’язання:

Нехай треба взяти х г 60-відсоткового розчину і у г 10-відсоткового розчину. Тоді загальна кількість розчину складає х+у=600 (г)

В х г 60-відсоткового розчину  міститься 0,6 х г кислоти, а в у г 30-відсоткового розчину  - 0,3у г солі, за умовою сумарна кількість повинна складати 40%  від 600 г , тобто 600∙0,4=240 (г) Тому, 0,6х+0,3у=240. Отримуємо систему:

х+у=600,                      х+у=600,         у=600-х;                х=200,          

0,6х+0,3у=240;           2х+у=800;         2х+600-х=800;     у=400.       

Відповідь: 200 г, 400 г.

 

3. Маємо два сплави міді і цинку. Перший сплав містить 9%, а другий  - 30% цинку. Скільки треба взяти кілограмів першого і скільки кілограмів другого сплавів, щоб отримати сплав масою 300 кг, що містить 23% цинку?

Розв’язання:

Нехай маса 9-відсоткового сплаву цинку  дорівнює х кг, а 30-відсоткового – у кг. Тоді х+у=300. Перший сплав містить  0,09х кг цинку, другий – 0,3у кг, а новий сплав 300∙0,23=69 (кг) цинку. Тоді 0,09х+0,3у=69. Маємо,

х+у=300,             х=300-у,                           х=300-у,                   

0,09х+0,1у=69;   0,09.(300-у)+0,3у=69;     27-0,09у+0,3у=69    

 

х=300-у;      х=100

0,21у=42;    у=200

Відповідь: 100 кг, 200 кг

4. Маємо два водно-сольових розчини. Перший розчин містить 25%, а другий – 40% солі. Скільки треба взяти кілограмів першого розчину і скільки кілограмів другого розчину, щоб отримати розчин масою 50 кг, що містить 34% солі?

Розв'язання:

Нехай маса 25-відсоткового розчину   дорівнює х кг, а 40-відсоткового – у кг. Тоді х+у=50. Перший розчин містить  0,25х кг солі, другий – 0,4у кг, а новий розчин 50∙0,34=17  (кг) солі. Тоді 0,25х+0,4у=17. Маємо,

х+у=50,                 х=50-у,                           у =50-х;                 

0,25х+0,4у=17;     0,25х + 0,4(50-х)=17;   0,25х+20-0,4х=17;           

у=50-х,             х=20,

0,15х=3;            у=30.

Відповідь: 20 кг, 30 кг.

5. У першому бідоні було молоко, масова частка жиру якого становила 3%, а в другому вершки, жирність яких  18 %. Скільки треба взяти молока і скільки вершків, щоб отримати 10 кг молока масовою часткою жиру 6%?

Розв’язання:

Нехай х кг і у кг – кількість молока і сливок, які треба взяти, щоб отримати молоко потрібної жирності. Тоді маса жиру молока складає – 3%∙х=0,03х (кг), вершків  18%∙у=0,18у (кг) . Загальна маса отриманого молока  дорівнює х+у=10 (кг), а маса жиру в отриманому молоці дорівнює 6%∙10=0,6 (кг).

Маємо систему:

х+у=10,                               х+у=10,              х=8;

0,03х+0,18у=0,6;                х+6у=20;            у=2.

Відповідь:8 кг молока , 2 кг вершків

6. Маємо два сплави золота і срібла. Один містить ці метали у співвідношенні 1:2, а другий – 2:3. Визначте яку кількість цих сплавів  потрібно взяти, щоб отримати 880 г нового сплаву, в якому співвідношення  золота і срібла складало б 17:27.

Розв’язання:

Нехай х – маса частини першого сплаву, у кг – маса частини другого сплаву. Концентрація золота в першому сплаві  дорівнює , а в другому - . Концентрація золота в остаточному сплаві дорівнює .

х+у=880,                х+у=880,           х+у=880,                 -5х-5у=-4400,

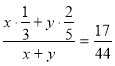
               5х+6у=5100,

у=700,

х=880-700=180.

Відповідь:180 г, 700 г.

7. Просушили 55 т зерна 16% вологості, після чого його 50т. Знайти відсоток вологості просушеного зерна.

Розв’язання:

1. 0,16∙55=8,8 (т)початковий вміст вологи.
2. 55-50 = 5 (т) – випарувалось вологи
3. 8,8 – 5 =3,8(т) – залишилось вологи в зерні
4. 3,8:50∙100=7,6% - відсоток вологи просушеного зерна

Відповідь: 7,6%

8. Вкладник поклав у банк 100 000 грн. під 10% річних. Яка сума буде нарахована через 7 років, за умови, що вкладник протягом даного часу не знімає гроші з рахунку?

Розв’язання:

а₀=100 000 грн.

р=7

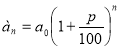
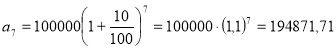(грн.)

Відповідь: 194 871, 71 грн.

Задача.

З гарячого крану ванна заповнюється за 23 хвилини. Із холодного крану за 17 хвилин. Маша відкрила спочатку гарячий кран. Через скільки хвилин вона повинна відкрити холодний кран, щоб до моменту наповнення ванни гарячої води налилося в 1,5 разів більше, ніж холодної

Розв’язання:

Позначимо об’єм ванни  - V.

Тоді:

Швидкість наповнення з гарячого крану V/23

Швидкість наповнення з холодного крану V/17

Виходячи з умови, що гарячої води налилось в 1,5 рази більше, ніж холодної, отримуємо, що

1,5x + x = 1

2,5x = 1

x = 0,4

Тобто гарячої води повинно бути 0,6 ванни, а холодної 0,4.

Так як швидкість заповнення гарячою водою дорівнює 23 хвилини, 0,6 ванни заповниться за

23 * 0,6  = 13,8 минут

Так як швидкість заповнення холодною водою дорівнює 17 хвилини, 0,4 ванни заповниться за

17 * 0,4 = 6,8 минут

Таким чином, оскільки загальне заповнення ванни дорівнює більшому з двох часів, то холодний кран потрібно відкрити за 6,8 хвилин до закінчення заповнення, тобто

13,8 - 6,8 = 7

Відповідь: через 7 хвилин

 

Задачі для самостійного розв’язку.

1. До розчину, який містив 20 г солі, додали 100 г води, після цього концентрація розчину зменшилась на 10%. Скільки грамів води містив розчин спочатку?   Відповідь: 80 г.

2. Скільки кілограмів 25-відсоткового і скільки кілограмів 50-відсоткового сплавів міді треба взяти, щоб отримати 20 кг 40-відсоткового сплаву?   Відповідь: 8кг 25% сплаву, 12 кг 50% сплаву.

3. Ціну товару знизили на 10%, а потім підвищили на 25%.  На скільки відсотків змінилась початкова ціна?

4. Меблева майстерня виготовляє стільці і столи. Стільці спочатку становили 80% обсягу продукції, а тепер 90%. На скільки відсотків при цьому зменшилось виробництво столів? Відповідь: на 50%.

5. Вологість свіжих грибів дорівнювала 99%. Коли гриби підсушили, то їх вологість знизилась до 98%. Як змінилась маса грибів?

6. Раніше 3 кг м’яса коштували стільки, скільки тепер коштують 2 кг. На скільки відсотків подорожчало м'ясо?

7. З молока виходить 25% вершків, а з вершків – 20% масла. Скільки треба мати молока, щоб одержати 10 кг масла?

8. Скільки грошей потрібно покласти в банк під 3% річних, щоб через три роки отримати більше , ніж 3000 грн.?

9. Через скільки років капітал вкладений в банк під 5 % річних, збільшиться у 2 рази?

10. Говорять, що в 1723 р. гетьман Полуботок поклав до англійського банку великий капітал з України під 4% річних. У скільки разів збільшився б той капітал з тих часів до наших днів?