Урок на тему "Визначні математичні задачі"

Про матеріал

Мета заняття: Познайомити учнів з різними етапами розвитку математичних задач різних епох і народів з стародавніх часів до нашого часу. Розкрити привабливість історії математики на прикладах стародавніх задач, теорем та алгоритмів їх розв’язування. Виховувати інтерес не тільки до вивчення математичних теорій, фактів, але й до історії виникнення і формування цих понять та теорій.

Перегляд файлу

Тема заняття: Визначні математичні задачі

Мета заняття: Познайомити учнів з різними етапами розвитку математичних задач різних епох і народів з стародавніх часів до нашого часу.

Розкрити привабливість історії математики на прикладах стародавніх задач, теорем та алгоритмів їх розв’язування.

Виховувати інтерес не тільки до вивчення математичних теорій, фактів, але й до історії виникнення і формування цих понять та теорій.

Обладнання: Презентація Microsoft Power Point.

Хід заняття:

Вступне слово вчителя.

Повідомлення теми та мети заходу.

Мотивація діяльності.

«Лейбніц застерігав, що хто хоче обмежитися сучасним без знання минулого, той ніколи не зрозуміє сучасного.

Перегорнемо сторінки минулого математичної науки».

Вступна задача.

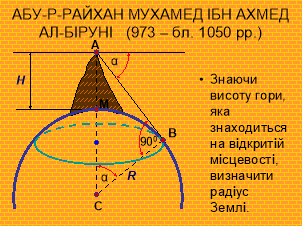
Перший учень:

Висвітлюється відповідний слайд.

Учень наводить приклад однієї з відомих задач про обчислення радіуса Землі, розповідає про спосіб розв’язання цієї задачі

АБУ – Р – РАЙХАНОМ МУХАМЕД ІБН АХМЕДОМ АЛ – БІРУНІ (973 – 1050 рр.)

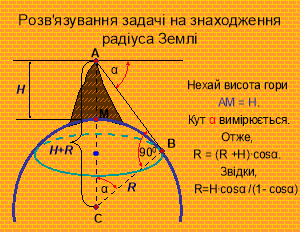
Етапи розв’язування задачі записуються на дошці, з наступною появою слайда з відповіддю.

Повідомлення учнів про розвиток математичної науки.

Другий учень:

Читає зміст наступних слайдів, розповідаючи про найвидатніші математичні тексти, що дійшли від цивілізацій Стародавнього сходу – Єгипту та Вавілону.

Розповідь про пам’ятки єгипетської математики.

Розв’язування задач.

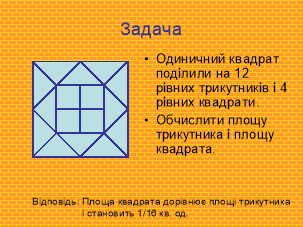
	Третій учень: «Переконаємось, що найбільші поклади математичних ідей, понять, задач, які потім об’єднувались у теорії, містяться у практичній діяльності людини». Читається умова однієї достатньо простої стародавньої задачі. Учням пропонується розв’язати цю задачу. Після швидкого обговорення висвітлюється прогнозоване пояснення та відповідь.
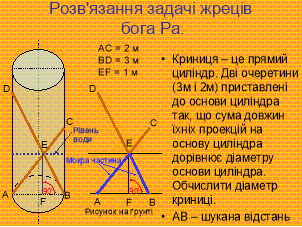
	Четвертий учень: «У 1912 році під час розкопок у дельті Ніла вчені виявили залишки храму, на стінах якого збереглися письмена. Були тут і математичні задачі. Текст цієї задачі жреці бога Ра вирізьбили на стіні велетенської кімнати, побудованої з гранітних брил. Задача була одним з випробувань для бажаючих стати жрецями бога Ра. Це був важкий і небезпечний іспит, про що відверто застерігали жреці».
	Четвертий учень: Розповідає про те, що цю задачу можна розв’язати аналітично, позначивши одну з невідомих відстаней іксом. Цей спосіб приводить до розв’язування рівняння четвертого степеня. Стародавні єгиптяни не знали ні теореми Піфагора, ні алгоритму розв’язування рівнянь четвертого степеня. Тому задачу жреців бога Ра вони розв’язували інакше.
	Четвертий учень: « На ґрунті креслили крейдою пряму і на відстані 1 метр від неї креслили другу. Потім опускали очеретини в криницю і позначали на них місце їх схрещення. Після цього очеретини клали на креслення так, щоб точка схрещення лежала на другій прямій, а очеретини починали обертати так, щоб мокрі кінці очеретин А і В попали на першу пряму. Після цього залишалося тільки виміряти наближено АВ, користуючись однією з очеретин».
	П’ятий учень: Продовжує розповідь про розвиток вавілонської культури, демонструючи джерело вивчення вавілонської математики – клинописні таблички. Більша частина математичних текстів – це посібники для учнів шкіл писців або вправи , які виконували писці й придворні чиновники. Ці тексти в основному починалися із слів: «роби, як робиться». Після чого наводився рецепт, як потрібно діяти.
	П’ятий учень: «Вавілонські математики зробили крок у розвитку всієї математики (квадратні рівняння – справжній зразок математичної теорії). Зробили крок і в розвитку геометрії. Квадрат і трикутник вавілоняни сприймали як абстрактні фігури, а про прямокутник говорили: «те, що має довжину й ширину», про трапецію – «лоб бика», про круг – «вигин», про сегмент – «поле півмісяця»». Розв’язується наступна задача.
	Шостий учень: «Учені Єгипту і Вавілона відкрили багато важливих математичних фактів, але наука розвивалася надзвичайно повільно. Приблизно на такому самому рівні були математичні знання і стародавніх греків. Але з VІ ст.. до н. е. грецька математика починає швидко збагачуватися новими фундаментальними знаннями. Греки перші прийшли до ідеї доведення і надали доведенням логічної форми, яка зберігається і тепер».
	Шостий учень: Розповідає про перших учених Античної Греції на прикладі Фалеса Мілетського, Піфагора Самоського.

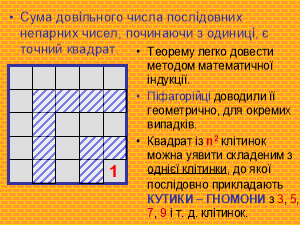
	Другий учень: Розв’язання задачі про суму довільного числа послідовних непарних чисел: «Нехай 2n + 1, 2n + 3, 2n + 5…- послідовні непарні числа. Доведемо, що сума довільного числа цих чисел є точний квадрат»… Доведення цього твердження геометричним способом, запропонованим піфагорійцями, є яскравим зразком красивого, елегантного розв’язання непростої алгебраїчної задачі..
	Третій учень: «У V столітті до н. д. були сформульовані три знамениті задачі. Спроби розв’язати їх засобами класичної геометричної алгебри й пошуки різних некласичних способів розв’язування спричинило виникнення нових математичних понять, способів і методів. Тільки в другій половині ХІХ ст.. математики дали вичерпну відповідь на запитання, поставлені давньогрецькими вченими в цих задачах».
	Третій учень: «Гіппократ Хіоський перший відкрив фігури, обмежені дугами кіл (серпики Гіппократа), сума площ яких рівновелика прямокутному трикутнику».
	Третій учень: Розв’язання задачі записується на дошці з наступним висвітленням розв’язку на дошці. Четвертий учень: Переглядаючи та читаючи наступні слайди, учні продовжують знайомство з розвитком математичної науки та з окремими визначними досягненнями.




Підсумок заняття. Домашнє завдання.
	Вчитель: «Математичні задачі практичного змісту відлиті в сучасні форми теоретичною думкою вчених різних епох і народів. Водночас пошуки розв’язків багатьох математичних задач не раз приводили вчених до відкриття нових математичних фактів».