Відстань у просторі.

Урок №1

Мета:систематизація знань учнів о відстані на площині та у просторі. Введення означення відстані між площинами та між двома мимобіжними прямими. Розвиток математичного мовлення, просторового уявлення учнів, графічної грамотності, охайності, вміння аналізувати. Виховання колективізму.

I Вивчення нового матеріалу

Одним з ключових понять геометрії є поняття відстані між точками. Воно має широке застосування в найрізноманітніших сферах життя людини – від високої науки до побуту і дозвілля. Використовується воно і тоді, коли розмірами реальних об’єктів, відстанню між якими цікавляться, за даних умов можна знехтувати. Так ми кажемо про відстань між зірками, планетами, передавачами та приймачами інформації, населеними пунктами, ядрами атома і електронами на орбіті тощо.

1.       Що розуміють під відстанню між двома точками? (довжина відрізка)

2.       ^{від точки до прямої, якщо точка не належить прямій?} (довжина перпендикуляра з цієї точки на пряму)

3.       від точки до прямої, якщо точка належить прямій? (відстань дорівнює нулю)

Оскільки всі інші відрізки з кінцями у даній точці і довільній точці прямої – похилі, то вони мають довжину більшу за довжину перпендикуляра. Тому кажуть, що відстань від точки до прямої – це довжина найменшого відрізка з усіх можливих, проведених з цієї точки до прямої. A

4. 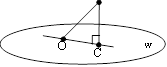      Що розуміють під відстанню від точки до площини, якщо ^{точка не належить площині?} (довжина перпендикуляра з цієї точки до площини)

5. 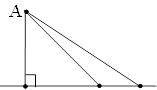      від точки до площини, якщо точка належить площині? (відстань дорівнює нулю) 6.Відстань від точки А до відрізка ВС визначається за таким алгоритмом: §            проводимо перпендикуляр АО з точки А на пряму ВС;

§    якщо основа О цього перпендикуляра належить даному

відрізку ВС, то шукана відстань дорівнює довжині відрізка АО;

§    в іншому випадку вона дорівнює довжині відрізка АВ або АС

O                   B C (залежно від того, яка з точок В чи С лежить ближче до точки О§                                       Аналогічно визначається відстань від точки до променя.⁾ 

Відстань між двома паралельними прямими дорівнює довжині спільного S1 A1 X h перпендикуляра цих прямих. Це випливає з того, що всі такі перпендикуляри АА₁=SS₁ рівні між собою, а кожний відрізок YX, який не є їхнім спільним перпендикуляром, має довжину, більшу від довжини

спільного перпендикуляра.                                                                                       ^{S A Y}

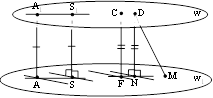Існують теореми про відстані між прямою і паралельною площиною, між паралельними площинами та мимобіжними прямими. Теорема про відстань між паралельними прямою і площиною:

відстань між паралельними прямою і площиною дорівнює

довжині спільного перпендикуляра, проведеного з якої-небудь точки прямої на площину.

Теорема про відстань між паралельними площинами: відстань між паралельними площинами дорівнює довжині спільного перпендикуляра, проведеного з якої-небудь точки однієї площини на другу площину.

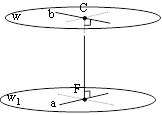Теорема про відстань між мимобіжними прямими: дві мимобіжні прямі мають спільний перпендикуляр і до того ж тільки один. Він є спільним перпендикуляром до паралельних площин, які проходять через ці мимобіжні прямі. Відстанню між мимобіжними прямими називається довжина спільного перпендикуляра.

Згідно з цим правилом потрібен спільний перпендикуляр до двох мимобіжних прямих. Спільним перпендикуляром до двох мимобіжних прямих називається відрізок з кінцями на цих прямих, перпендикулярний до кожної з них.

II Закріплення.

M

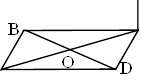
1. Дано квадрат ABCD, діагоналі якого перетинаються в точці C

О. Пряма МС перпендикулярна до площини квадрата. Доберіть до кожної пари мимобіжних прямих відрізок, що A виражає відстань між ними.

§    AB ^і MC (у квадраті кути прямі, тому BC_⊥BA, за означенням перпендикулярності прямої та площини BC_⊥MC_⇒BC – спільний перпендикуляр)

§    AD ^і MC (у квадраті кути прямі, тому DC_⊥AD, а означенням перпендикулярності прямої та площини DC_⊥CM_⇒DC – спільний перпендикуляр)

§               BD і MC (у         квадраті     діагоналі    перпендикулярні,     тому    OC⊥BD, перпендикулярності прямої та площини OC⊥MC⇒OC – спільний перпендикуляр)

а

означенням

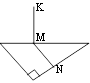2. У прямокутному трикутнику ∆АВС (∠С=90°) через точку М – середину гіпотенузи АВ проведено MNAC (M∈AB, N∈BC).

Точка К∉(АВС), КМ – перпендикуляр до площини трикутника. AB

Укажіть відрізок, що є відстанню від точки К до прямої ВС та

                знайдіть його, якщо АС=24 см, КМ=12 см.                                                   C

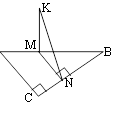Відповідь: Проведемо відрізок KN. Розглянемо _∆KMN. KM – перпендикуляр до площини, KN - похила, MN – проекція. За властивістю паралельних прямих, якщо ∠С=90°і MNAC, тоді і ∠MNB=90°. Тоді за теоремою про три перпендикуляри, якщо проекція MN⊥BC, тоді і похила KN⊥BC. Відрізок KN – є

відстанню від точки К до прямої ВС.                                                                                   A

Якщо через точку М – середину гіпотенузи АВ проведено MNAC (M∈AB, N∈BC), тоді за теоремою Фалеса точка N∈BC середина сторони. За означенням середньої лінії трикутника, MN – середня лінія і за властивістю MN=AC_×0,5=12 см. За теоремою Піфагора знайдемо KN.

 

Відстань у просторі. Властивість точки, рівновіддаленої від вершин та сторін многокутника. Урок №2-3

Мета:Контроль та закріплення отриманих знань. Розвиток математичного мовлення, кмітливості, допитливості, графічної грамотності, вміння узагальнювати отриманні знання, порівнювати. Виховання самостійності, зосередженості, наполегливості до праці.

Самостійна робота за темою «Кути і відстань у просторі»

(1-6 завдання по 1 балу, 7-9 завдання по 2 бали)

Варіант №1

1.                   Чи може кут між прямою і площиною бути 146°? (ні, бо 0⁰ ≤∠(aw) ≤ 90⁰)

2.                   У якому випадку кут між прямою і площиною дорівнює 0°? (якщо пряма

паралельна площині або належить їй)

3.                   Чи залежить кут між мимобіжними прямими від вибору прямих, які перетинаються? (кут не залежить від вибору прямих, що перетинаються, оскільки

паралельне перенесення зберігає рівність відповідних кутів з паралельними сторонами.)

4.                   Чи може двогранний кут бути тупим? (ні, бо 0⁰ ≤∠(nm) ≤ 90⁰)

5.                   Що розуміють під відстанню від точки до площини, якщо точка не належить площині? (довжина перпендикуляра з цієї точки до площини)

6.                   Сформулюйте теорему про відстань між мимобіжними прямими.

7. 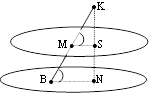                  Чи правильно, що пряма, яка перетинає паралельні площини, перетинає їх під однаковими кутами? Поясніть відповідь. (так тому, що пряма нахилу є похилою і разом зі спільним перпендикуляром утворює єдину площину. Якщо дві паралельні площини перетинаються третьою площиною, то прямі перетину

паралельні і відповідні кути при паралельних MSBN прямих рівні)

8.                   Дано ромб ABCD, діагоналі якого перетинаються в точці О. Пряма МС перпендикулярна до площини ромба. Доберіть до пари мимобіжних прямих BD і MC відрізок, що виражає відстань між ними. Поясніть відповідь. (у ромбі діагоналі перпендикулярні, тому OC⊥BD, за означенням перпендикулярності прямої та площини OC⊥MC⇒OC

– спільний перпендикуляр)

9. Із вершини В квадрата ABCD проведено перпендикуляр ВМ до площини квадрата. Пряма АМ утворює з площиною квадрата кут 45°. Знайти кут між прямою MD і площиною квадрата, якщо АВ=8 см.

Варіант №2

1.                        В яких межах знаходиться кутова міра кута між прямими, що ^{перетинаються?}(не перевищує 90°)

2.                        Як знайти кут між похилою і площиною, до якої вона проведена?

3.                        Яку фігуру утворюють основи всіх можливих похилих, проведених до

площини з однієї точки під однаковими кутами? (коло)

4.                        Чи можна говорити, мимобіжні прямі взаємно перпендикулярні? (про перпендикулярність мимобіжних прямих не кажуть, оскільки витримується означення поняття перпендикулярних прямих.)

5.                        Що розуміють під відстанню між двома точками?

(довжина відрізка)

6.                        Що розуміють під відстанню від точки до площини, якщо точка належить площині? (відстань дорівнює нулю)

7.                        Чи правильно, що площина, яка перетинає паралельні площини, перетинає їх під однаковими кутами? Поясніть відповідь. (Так. При перетині двох паралельних площин третьою, прямі перетину паралельні nd. Нехай деяка пряма s у цій третій площині перетинає ці прямі під прямим кутом n⊥s, s⊥d. З точок перетину проведемо у паралельних площинах прямі m⊥nі k⊥d. Ці дві нові прямі утворюють разом єдину площину, яка перетинає паралельні площини по цим паралельним прямим mk. Пряма s розташована у новій площині, бо має з нею дві спільні точки. Як січна, вона утворює з цими прямими рівні відповідні кути за властивістю паралельних прямих у площині ∠(s,m)=∠(s,k). Ці кути і є за означенням лінійні кути між площинами)

8.                        Дано прямокутник ABCD, діагоналі якого перетинаються в точці О. Пряма МС перпендикулярна до площини прямокутника. Доберіть до пари мимобіжних прямих AB і MC відрізок, що виражає відстань між ними. Поясніть відповідь. (у прямокутнику кути прямі, тому BC⊥BA, за означенням перпендикулярності прямої та площини

BC_⊥MC_⇒BC – спільний перпендикуляр)

9.                        Із вершини С прямокутника ABCD проведено до площини перпендикуляр

СК. Пряма ВК утворює з площиною прямокутника кут 30°. Знайти кут між прямою АК і площиною прямокутника, якщо АВ=16 см, ВС=12 см. Варіант №3

1.                        Чому дорівнює кут між перпендикулярними прямими? Паралельними прямими? (90^°, 0^°)

2.                        Який кут називають кутом між прямою і площиною? (кут між прямою і її проекцією на площину)

3.                        Дайте означення кута між двома площинами, які перетинаються. (це кут між двома прямими, які належать цим площинам і перпендикулярні до прямої їхнього перетину.)

4.                        Що розуміють під відстанню від точки до прямої, якщо точка належить

прямій? (відстань дорівнює нулю)

5.                        Що таке спільний перпендикуляр між мимобіжними прямими?

6.                        Сформулюйте теорему про відстань між прямою і паралельною площиною.

7.                        Чи можуть дві похилі, проведені з однієї точки до площини, що мають різну довжину, бути нахиленими до цієї площини під однаковим кутом? Поясніть відповідь.

(ні, бо маємо різні значення синусів відповідних кутів, так як синус гострого кута - це відношення протилежного катета, тобто перпендикуляра до гіпотенузи, тобто похилої)

8.                        Дано квадрат ABCD, діагоналі якого перетинаються в точці О. Пряма МС перпендикулярна до площини квадрата. Доберіть до пари мимобіжних прямих AD і MC відрізок, що виражає відстань між ними. Поясніть відповідь. (у квадраті кути прямі, тому DC_⊥AD, за означенням перпендикулярності прямої та площини DC_⊥CM_⇒DC – спільний перпендикуляр)

9.                        Із вершини Н квадрата AНCD проведено перпендикуляр НМ до площини квадрата. Пряма АМ утворює з площиною квадрата кут 60°. Знайти кут між прямою MD і площиною квадрата, якщо АН=10 см.

Варіант №4 1. Що називають кутом між прямими? (менший з кутів, які утворюють дві прямі при перетині)

2.                        Коли говорять про кут нахилу прямої до площини? (коли пряма перетинає площину)

3.                        Дайте означення кута між мимобіжними прямими? (кут між прямими, які перетинаються і відповідно паралельні даним мимобіжним прямим)

4.                        Чому дорівнює кут між паралельними площинами? (0_°)

5.                        Що розуміють під відстанню від точки до прямої, якщо точка не належить прямій? (довжина перпендикуляра з цієї точки на пряму)

6.                        Сформулюйте теорему про відстань між паралельними площинами.

7.                        Чи правильно, що пряма, яка перетинає паралельні площини, перетинає їх під однаковими кутами? Поясніть відповідь. (так тому, що пряма нахилу є похилою і разом зі спільним перпендикуляром утворює єдину площину. Якщо дві паралельні площини перетинаються третьою площиною, то прямі перетину

паралельні і відповідні кути при паралельних MSBN прямих рівні)

8.                        Дано ромб ABCD, діагоналі якого перетинаються в точці О. Пряма МС перпендикулярна до площини ромба. Доберіть до пари мимобіжних прямих BD і MC відрізок, що виражає відстань між ними. Поясніть відповідь. (у ромбі діагоналі перпендикулярні, тому OC⊥BD, за означенням перпендикулярності прямої та площини OC⊥MC⇒OC

– спільний перпендикуляр)

             9.         Із вершини Р прямокутника ABРD проведено до площини перпендикуляр РК.

Пряма ВК утворює з площиною прямокутника кут 45°. Знайти кут між прямою АК і площиною прямокутника, якщо АВ=4 см, ВР=6 см.

II Нова темаТеореми про точку, рівновіддалену від вершин многокутника:

Якщо через центр кола, описаного навколо многокутника, проведено пряму, перпендикулярну до площини многокутника, то кожна точка цієї прямої рівновіддалена від вершин многокутника.

Якщо деяка точка рівновіддалена від вершин многокутника, то основа перпендикуляра, опущеного з даної точки на площину многокутника, збігається з центром кола, описаного навколо многокутника.

Центр описаного кола – це точка перетину серединних перпендикулярів до сторін многокутника, а радіус – відрізок, що сполучає центр з вершиною многокутника.

Положення центра описаного кола та радіуси описаного кола:

В гострокутному трикутнику центр внутрішній, у тупокутному – зовнішній центр, у прямокутному – на середині гіпотенузи. У прямокутнику та квадраті центр розташовано на перетині діагоналей, описати коло можливо навколо рівнобедреної трапеції. Радіуси знаходяться за формулами:

Довільний трикутник Прямокутний трикутник

                                                  R = abc ;                                  відношення сторониR = c ;               с − гіпотенуза

                                  4^S                                до подвоєного синуса протилежного кута2

Правильний трикутник                 Правильний чотирикутник Правильний шестикутник

R = a3 R = a2 R = a

Теореми про точку, рівновіддалену від сторін многокутника:

Якщо через центр кола, вписаного в многокутник, проведено пряму, перпендикулярну до площини многокутника, то кожна точка цієї прямої рівновіддалена від сторін многокутника.

Якщо деяка точка рівновіддалена від сторін многокутника, то основа перпендикуляра, опущеного з даної точки на площину многокутника, збігається з центром кола, вписаного в многокутник.

Центр вписаного кола – це точка перетину бісектрис внутрішніх кутів многокутника, а радіус – перпендикулярний відрізок з центра до сторони. Положення центра вписаного кола та радіуси вписаного кола:

Якщо у опуклого чотирикутника суми довжин протилежних сторін рівні, у нього можна вписати коло. У прямокутнику, ромбі та квадраті центр розташовано на перетині діагоналей, вписати коло можливо у деяку трапецію. Радіуси знаходяться за формулами:

Довільний многокутник Ромб Трапеція 

S = rp,     де                р − півпериметр r = h;                                h −висота r = h;                     h −висота

22

Правильний трикутник Правильний чотирикутник шестикутн^{Правильний} ик

r = 2a3 = R2 r = ^a2 r ₌ a23

У правильних многокутниках центри описаного і вписаного кола співпадають.

III Закріплення.

1.                        Точка М віддалена від вершин квадрата зі стороною 6 _смна 2 см. Чому дорівнює відстань від точки М до площини квадрата?

2.                        Точка В віддалена від усіх сторін правильного трикутника на 12 см, а від площини трикутника на 3 см. Чому дорівнює сторона трикутника?

3.                        Точка О – центр квадрата зі стороною 4 см, ОА – пряма, що перпендикулярна до площини квадрата, ОА=5 см. Знайдіть відстані від точки А до сторін та вершин квадрата та кути між цими прямими і площиною квадрата.

4.                        Відстань від точки Р до сторін правильного трикутника дорівнює 10 см. Знайдіть відстані від точки Р до площини трикутника і до вершин трикутника, якщо сторона трикутника дорівнює 163 см .

5.                        Кут між площинами aі βдорівнює 30°. Точка А, яка лежить у площині a, віддалена від лінії перетину площин на 12см. Знайдіть відстань від проекції точки А на площину β до лінії перетину площин.

Відстань та кути у просторі. Властивість точки, рівновіддаленої від вершин та сторін многокутника.

Урок №4-5

Мета: Контроль та закріплення отриманих знань. Розвиток математичного мовлення, кмітливості, допитливості, графічної грамотності, вміння узагальнювати отриманні знання, порівнювати. Виховання самостійності, зосередженості, наполегливості до праці.

Самостійна робота за темою «Властивості точки, рівновіддаленої від вершин та сторін многокутника»

(1-6 завдання по 1 балу, 7-8 завдання по 3 бали)

Варіант №1

1.                   Де розташовано центр кола, вписаного у трикутник?

2.                   Запишіть формулу знаходження радіуса кола, вписаного у многокутник.

3.                   Де розташовано центр кола, описаного навколо прямокутника?

4.                   Що розуміють під відстанню від точки до площини, якщо точка не належить площині?

5.                   Дайте означення кута між двома площинами, які перетинаються.

6.                   Сформулюйте теорему про відстань від точки поза площиною до сторін многокутника.

7.                   Точка С віддалена від вершин прямокутника зі сторонами 5 см _та 3 _смна 5 см. Чому дорівнює відстань від точки С до площини прямокутника?

8.                   Кут між площинами αі βдорівнює 30°. Точка А, яка лежить у площині α, віддалена від лінії перетину площин на 12см. Знайдіть відстань від проекції точки А на площину β до лінії перетину площин.

Варіант №2 1.   Де розташовано центр кола, вписаного у ромб?

2.                        Запишіть формулу знаходження радіуса кола, вписаного у правильний чотирикутник.

3.                        Навколо якої трапеції можливо описати коло?

4.                        Чи можна говорити, мимобіжні прямі взаємно перпендикулярні?

5.                        Що розуміють під відстанню між двома точками?

6.                        Сформулюйте теорему про пряму, проведену у центр вписаного кола, перпендикулярно до площини многокутника.

7.                        Точка А віддалена від усіх сторін правильного трикутника на 21 см , а від площини трикутника на 4 см. Чому дорівнює сторона трикутника?

8.                        Кут між площинами αі βдорівнює 30°. Знайдіть відстань від точки М, яка лежить у площині α, до лінії перетину площин, якщо проекція точки М на площину βвіддалена від лінії перетину площин на 6 см.

Варіант №3

1.                   Де розташовано центр кола, описаного навколо трапеції?

2.                   Запишіть формулу знаходження радіуса кола, описаного навколо правильного трикутника.?

3.                   Де розташовано центр кола, описаного навколо прямокутного трикутника?

4.                   В яких межах знаходиться кутова міра кута між прямими, що перетинаються?

5.                   Що таке спільний перпендикуляр між мимобіжними прямими?

6.                   Сформулюйте теорему про пряму, проведену у центр описаного кола, перпендикулярно до площини многокутника.

7.                   Точка Р віддалена від сторін квадрата на 15 см. Чому дорівнює довжина сторони квадрата, якщо відстань від точки Р до площини 10 см?

8.                   Кут між площинами αі βдорівнює 60°. Точка О, яка лежить у площині α, віддалена від лінії перетину площин на 4 см. Знайдіть відстань від проекції точки О на площину β до лінії перетину площин.

Варіант №4

1.                   Де розташовано центр кола, описаного навколо квадрата?

2.                   Запишіть формулу знаходження радіуса кола, описаного навколо прямокутного трикутника.

3.                   Де розташовано центр кола, вписаного у трикутник?

4.                   Дайте означення кута між мимобіжними прямими.

5.                   Що розуміють під відстанню від точки до прямої, якщо точка не належить прямій?

6.                   Сформулюйте теорему про відстань від точки поза площиною до вершин многокутника.

7.                   Точка В віддалена від усіх вершин правильного трикутника на 12 см, а від площини трикутника на 2 см. Чому дорівнює сторона трикутника?

8.                   Кут між площинами αі βдорівнює 60°. Знайдіть відстань від точки М, яка лежить у площині α, до лінії перетину площин, якщо проекція точки М на площину βвіддалена від лінії перетину площин на 5 см.

Варіант №5

1.              Який відрізок буде радіусом кола, вписаного у трикутник?

2.              Запишіть формулу знаходження радіуса кола, вписаного у квадрат.

3.              Де розташовано центр кола, описаного навколо прямокутника?

4.              Що розуміють під відстанню між паралельними площинами?

5.              Дайте означення кута між двома прямими, які перетинаються.

6.              Сформулюйте теорему про відстань від точки поза площиною до сторін многокутника.

7.              Точка С віддалена від вершин прямокутника зі сторонами 2 см та 3 смна 5 см. Чому дорівнює відстань від точки С до площини прямокутника?

8.              Кут між площинами αі βдорівнює 30°. Точка А, яка лежить у площині α, віддалена від лінії перетину площин на 12см. Знайдіть відстань від проекції точки А на площину β до лінії перетину площин.

Варіант №6 1.   Де розташовано центр кола, вписаного у трикутник?

2.                        Запишіть формулу знаходження радіуса кола, вписаного у правильний шестикутник.

3.                        Навколо якої трапеції можливо описати коло?

4.                        Чи можна говорити, мимобіжні прямі взаємно перпендикулярні?

5.                        Що розуміють під відстанню між паралельними прямими?

6.                        Сформулюйте теорему про пряму, проведену у центр вписаного кола, перпендикулярно до площини многокутника.

7.                        Точка А віддалена від усіх сторін правильного трикутника на 21 см , а від площини трикутника на 4 см. Чому дорівнює сторона трикутника?

8.                        Кут між площинами αі βдорівнює 60°. Знайдіть відстань від точки М, яка лежить у площині α, до лінії перетину площин, якщо проекція точки М на площину βвіддалена від лінії перетину площин на 6 см. II Закріплення. 1. Із вершини Р прямокутника ABРD проведено до площини перпендикуляр РК. Пряма ВК утворює з площиною прямокутника кут 45°. Знайти кут між прямою АК і площиною прямокутника, якщо АВ=4 см, ВР=6 см.

2.                        Точка О – центр квадрата зі стороною 4 см, ОА – пряма, що перпендикулярна до площини квадрата, ОА=5 см. Знайдіть відстані від точки А до сторін та вершин квадрата та кути між цими прямими і площиною квадрата.

3.                        Відстань від точки Р до сторін правильного трикутника дорівнює 10 см. Знайдіть відстані від точки Р до площини трикутника і до вершин трикутника, якщо сторона трикутника дорівнює 16 3 см .

4.                        Кут між площинами αі βдорівнює 30°. Точка А, яка лежить у площині α, віддалена від лінії перетину площин на 12см. Знайдіть відстань від проекції точки А на площину β до лінії перетину площин.

5.                        Із вершини Н квадрата AНCD проведено перпендикуляр НМ до площини квадрата.

Пряма АМ утворює з площиною квадрата кут 60°. Знайти кут між прямою MD і площиною квадрата, якщо АН=10 см.

6. 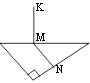                       У прямокутному трикутнику ∆АВС (∠С=90°) через точку М – середину гіпотенузи АВ проведено MNAC (M∈AB, N∈BC). Точка

К∉(АВС), КМ – перпендикуляр до площини трикутника. Укажіть відрізок, AB що є відстанню від точки К до прямої ВС та знайдіть його, якщо АС=24 см,

       КМ=12 см.                                                                                                                                       C

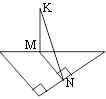Відповідь: Проведемо відрізок KN. Розглянемо ∆KMN. KM – перпендикуляр до площини, KN - похила, MN – проекція. За властивістю паралельних прямих, якщо ∠С=90° і MNAC, тоді і ∠MNB=90°. Тоді за теоремою про три перпендикуляри, якщо проекція

MN⊥BC, тоді і похила KN⊥BC. Відрізок KN – є відстанню від точки К до прямої ВС. AB Якщо через точку М – середину гіпотенузи АВ проведено MNAC (M∈AB, N∈BC), тоді за теоремою Фалеса точка N∈BC середина сторони. За означенням середньої

лінії трикутника, MN – середня лінія і за властивістю MN=AC×0,5=12 см. За ^C

теоремою Піфагора знайдемо KN.