Використання активних методів навчання у вигляді тренінгів

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

ДВНЗ «ПРИАЗОВСЬКИЙ ДЕРЖАВНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ»

МАРІУПОЛЬСЬКИЙ МЕХАНІКО-МЕТАЛУРГІЙНИЙ КОЛЕДЖ

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Методична розробка

 

«Використання активних методів навчання

у вигляді тренінгів»

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Маріуполь

2019

Петергера Є.В. Методична розробка «Використання активних методів навчання у вигляді тренінгів».

 

Викладено методику відкритого заняття з елементами тренінгу. Викладач використовує тренінги практично на всіх етапах заняття: під час актуалізації опорних знань студентів, під час викладання нового матеріалу,  тренінг на закріплення нового матеріалу. З метою активності студентів на занятті викладач використовує одночасно  види опитування: індивідуальну самостійну роботу на ЕОМ, фронтальне опитування,  розв’язування задач.

 

      Методичні рекомендації призначені насамперед  для  викладачів спеціальності «Розробка програмного забезпечення» та можуть бути корисними  для студентів ВНЗ І-ІІ рівнів акредитації.

 

Рецензенти:   Солнцева С.О., голова Маріупольського регіонального методичного об’єднання  викладачів інформатики;

 

                        Красковська Н.О., голова циклової комісії спеціальних дисциплін програмування, спеціаліст вищої категорії

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Розглянуто та схвалено на засіданні

циклової  комісії «Розробка програмного забезпечення»

Протокол №      від   «   »               2019р. Голова комісії _____ О.М.Кривощшеєва

 

ЗМІСТ

 

Вступ ……………………………………………………………………….….…3

План-конспект заняття…………………………………………………..……...4

Висновки …………………………………………………………………….….14

Література ……………………………………………………………………....15

Додатки  ……………………………………………………………….………..16

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ВСТУП

 

   Ефективність реформування системи освіти і професійної підготовки залежить від уміння навчального закладу швидко переорієнтувати старі ідеї і шаблони на задоволення професійних потребу галузі. Якщо великий досвід педагогічного колективу уміло направити на зміну потреб суспільства в підвищенні якості людського капіталу як сукупностей якостей людини, що ґрунтуються на природних здібностях, високому рівні освіти, компетентності, мобільності та умінні реагувати на виникаючі зміни, то конку­рентоспроможність сучасних випускників буде гарантованою на ринку праці.

    Методи активного навчання вченими й практиками розуміються як такі способи організації педагогічного процесу у ВНЗ, які максимально активізують діяльність і студентів, і викладачів, стимулюють їх до виявлення активності й самостійності, потреб самореалізації та саморозвитку. Їх поділяють на імітаційні та неімітаційні методи навчання. До імітаційних (імітація з лат. мови – imitato – наслідування, підробка – відтворювання реального явища, процесу, об’єкта, ситуації, діяльності) методів навчання відносяться ігрові методи: ділова гра, дидактичні ігри, ігрові ситуації, ігрові процедури й прийоми, стажування з виконанням посадової ролі, імітаційний тренінг, ігрове проектування, розігрування ролей, студентський театр, психодрама; неігрові методи -  тренаж на робочому місці, реальне проектування, науково-дослідницька робота. Такі методи навчання як аналіз конкретної професійної ситуації (індивідуальний і груповий), вирішення виробничих завдань можуть реалізовуватися в ігрових і неігрових формах. До неімітаційних методів навчання – проблемна лекція, дискусії, програмоване навчання, виїздні заняття (в школу, на виробництво), випускна (дипломна) робота на реальній основі, стажування без виконання посадової ролі.

    Підвищення якості підготовки майбутніх фахівців вимагає актуалізації їх навчально-пізнавальної діяльності, стимулювання до максимально повного розкриття і реалізації внутрішнього потенціалу в професії. Актуалізація педагогічного процесу у вищому навчальному закладі за рахунок використання методів навчання сприяє позитивному ставленню студентів до майбутньої професії, виявленню активності в засвоєнні професійних знань і вмінь, формуванню активної позиції щодо професійного самовдосконалення і саморозвитку впродовж всього життя.

  Сучасне спілкування з молоддю потребує нових форм і методів. Як інновацію можна використовувати тренінги. Слово «тренінг» походить від англійської “train”, що означає «навчати», «тренувати». Тренінг відрізняється від традиційних форм навчання (лекцій, семінарів) практичною спрямованістю та активністю кожного з тих, хто бере в ньому участь. Присутні не тільки знайомляться з корисною для себе інформацією, але й навчаються використовувати отримані знання на практиці, легко засвоюють новий матеріал.

        Проведення тренінгу базується на принципах:

• активності,
• творчої позиції (особистісних змін і розвитку),
• усвідомлення поведінки,
• партнерського спілкування,
• особливості роботи тренера.

Тренінги сприяють спілкуванню, впевненості в собі, наполегливості, критичності мислення, розвитку ідентичності, вирішенню проблем і прийняття рішень, емоційному самоконтролю.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

                                                       План заняття

     Дисципліна: Математичні методи дослідження операцій

 Спеціальність: «Розробка програмного забезпечення»

Блок змістових модулів: 5.5  Математичні методи дослідження операцій

     Модуль змістовний: КЗН.02.02.03 Постановка та властивості транспортної

                                      задачі лінійного програмування

Модульна одиниця: Транспортна задача

Мета заняття.

Методична: використання активних методів навчання у вигляді тренінгів.

 Дидактична:

навчальна: оволодіти уміннями та навичками вирішення виробничих та економічних задач  методами транспортної задачі;

розвивальна: підвести студентів до суперечливості різновидів методу з пропозицією самим знайти спосіб розв’язання задач, розвивати логічне мислення.

виховна: виховувати у студентів самостійність, активність, творчу ініціативу при обиранні середи програмування та розробці програм, прищеплювати повагу до обраної спеціальності.

Вид заняття: лекція.

Тип заняття:  лекція з елементами тренінгу

Форми та методи проведення заняття: індивідуальна самостійна робота на ЕОМ, фронтальне опитування, тренінг під час актуалізації опорних знань студентів, тренінг під час викладання нового матеріалу, розв’язування задач, тренінг на закріплення нового матеріалу.

Міждисциплінарні зв’язки:

Забезпечувальні:   Вища математика, Операційні системи, Офісне програмне

                                 забезпечення, Основи програмування та алгоритмічні мови,

                                 Математична логіка, Теорія ймовірностей і математична

                                 статистика, Чисельні  методи.

Забезпечувані:   Основи програмної інженерії, Конструювання програмного

                         забезпечення, Статистичне моделювання і прогнозування

       Методичне забезпечення : дидактичні картки з варіантами задач, програмне забезпечення  «Математичний редактор MathCAD», перелік питань до тренінгів, питання до фронтального опитування .   

Технічні засоби навчання:  персональні електронні  обчислювальні машини

Література. Основна:   Бугір М.К. Математика для програмістів, підручник ,           К: 2003,  

                                      Єрмаков І.І.  Довідник з математики., К: 1998

                       Додаткова: Руденко В.Д.  Курс інформатики, підручник, К: 2004

                                       Симонович А.І. Комп’ютерна техніка, М: 2001

 

 

 

 

Зміст і хід заняття:

 

1.         Організаційна частина 5хвилин

•         привітання студентів ;
•         перевірка готовності студентів, аудиторії та обладнання до занять. На дошці записана тема заняття і план, на партах роздатковий матеріал, на ЕОМ  підготовлено необхідне програмне забезпечення;
•         перевірка присутніх студентів: перекличка за навчальним журналом групи;
•         «Техніка безпеки». Викладач нагадує студентам про головні моменти безпечної роботи на ЕОМ.

 

 

2.         Актуалізація опорних знань.

     Викладач одночасно перевіряє знання студентів через роботу на ЕОМ та проводить фронтальне опитування. До 10 хвилин.

 

 2.1 Індивідуальна самостійна робота на ЕОМ - виконують студенти за ЕОМ. Вони виконують практичне завдання на ЕОМ в математичному редакторі MathCAD, оцінки будуть повідомлені після закінчення роботи. Але студенти можуть заробити додаткові бали, якщо братимуть активну участь у тренінгах під час викладання нової теми та під час закріплення нового матеріалу, про що їм повідомляє викладач.

 

                                  Питання до роботи на ЕОМ:

1.  На якому етапі постанови виконується формалізація задачі?
2.  Як змінити задачу мінімізації на максимізації?
3.  Які параметри завжди керовані?
4.  На якому етапі користувач уточнює дані, яких бракує, для постанови?
5.  До якого моделювання можна віднести функцію помноження?
6.  Як називають моделі різної природи, але з однаковими рівняннями?
7.  На якому етапі постанови задачі виконується адаптація моделі?
8.  В яких моделях усі параметри некеровані?
9.  До якого моделювання  відноситься функція y=5*x-3 ?

10) В яких моделях усі параметри означені  відносно часу?

11.  Як називається вектор, який вказує напрям до екстремуму?
12.  Який знак в обмеженнях для задачі максимізації?
13. Для двох рівнянь та двох невідомих скільки кроків жорданових виключень?
14.  Якщо ісходна задача мінімізації, то двоїста………….?
15. В якому методі додають зміні х₃, х₄, х₅ ?
16.  Для чого використовують жорданові виключення ?                                                                    
17.  Якщо гра надана у вигляді матриці, то скільки кроків можуть брати участь?

18) В якому методі використовують крок h ?

19) кільки кроків (ітерацій) виконується в методі Лагранжа

20)  Що необхідно задати в умові зокрема функції в методі Лагранжа?

21) В якому методі до екстремуму рухаються паралельно до осей координат ?

22) Стратегія (0, 1, 0, 0) це чиста або змішана ?

23)  Як називається гра, яка спрямована на сумарний виігриш усіх кроків?

     24)  В парній грі задача першого кроку максимально виіграти, а у другого ?

25)  Стратегія (1/5, 2/5, 0, 2/5) це чиста чи змішана ?

26) Як називається гра, яка спрямована на індивідуальний виігриш ?

27) Як називається набір ймовірностей успішних кроків з загального числа кроків?

28) Наведіть приклад коаліційної гри ?

29)  Наведіть приклад некоаліційної гри ?

30)  Чому дорівнює сума набору ймовірностей 0 чи 1 ?

31) Який метод швидше надає результат: покоординатного спуску чи найшвидшого спуску?

32)  Що необхідно задати зокрема функції у методі покоординатного спуску?

33) Яки знак ставлять перед функцією в методі Лагранжа для задачі максимізації ?

34) Перед чим в функції Лагранжа ставлять λ перед функцією чи обмеженням?

35) В якому методі найшвидшого зниження крок розраховується зі змінним чи

     постійним кроком ?

 36)  В якому методі найбільша ймовірність перейти екстремум ?

Приклад виконання практичного завдання дивись у додатку А.

 

       2.2 Фронтальне опитування. Під час опитування студентів викладач нагадує їм деякі особливі моменти з попередніх тем, коментує найтиповіші помилки. Крім того, під час відповідей викладач акцентує увагу на математичні підстави.

Питання до фронтального опитування:

1.  Запишіть в MathCAD  для побудови графіка [-3…..3]
2.  Для чого використовується знак у MathCAD ?
3.  Якою клавішею виділити увесь вираз?
4.  Яка команда задається перед рішенням системи рівнянь?
5.  Яка команда задається після запису системи рівнянь?
6.  Що потрібно записати на початку перед рішенням системи рівнянь?
7.  Команда find (x,y) використовується для вирішення одного рівняння чи

      системи?

8.  Для чого використовується команда format під час побудови графіків?
9. Чи можна на одному аркуші  виконати декілька завдань ?

10) Який знак замість = можна також ставити для розрахунків?

 

2.3 Проведення тренінгу з питання: «Яке програмне забезпечення краще використовувати для простих математичних операцій: математичний редактор MathCAD чи табличний процесор Excel». Група розподіляється на 2 підгрупи за принципом: парні номери у навчальному журналі прізвищ в 1-ій підргупі, непарні – в 2-ій. Після закінчення опитування викладач оголошує результати. Але студенти можуть заробити додаткові бали, якщо братимуть активну участь під час викладання нової теми та під час закріплення нового матеріалу. До 10 хвилин.

 

2.4 Коментар результатів індивідуальної самостійної роботи студентів на ЕОМ

     робить викладач.

 

3.         Повідомлення теми та мети заняття. Тема записана на дошці та усно повідомляється викладачем.

 

4.         Мотивація вивчення теми.

Проводиться у формі бесіди, де викладач акцентує увагу і ставить перед студентами завдання, які вони повинні розв’язати: знати постанову транспортної задачі, алгоритм методу та вміти складати програми на ЕОМ, щоб отримувати оброблені дані. Викладач пояснює необхідність проведення заняття з елементами тренінгу, це пов’язано з тим, що методи, які вивчаються за дисципліною: «Математичне методи дослідження операцій», необхідно розв’язувати за допомогою ЕОМ, використовуючи різні середовища програмування, які вивчаються за дисципліною «Основи програмування та алгоритмічні мови». А правильно обрати ту, чи іншу мови програмування можна через тренінг, в проведенні якого студенти будуть брати участь. І взагалі, згідно Стандарту вищої освіти, необхідно після отримання виробничої чи економічної задачі розробити її постановку за існуючими алгоритмами та методами вирішення, а після скористуватися мовою програмування чи системою проектування програм для розробки програми. А принципи роботи систем проектування будуються на мовах програмування, наприклад, Delphi, яку студенти будуть вивчати.

 

5.         Викладання нового матеріалу.

     Лекція з практичною демонстрацією вирішення задачі. До 35 хвилин.

План лекції:

1. Постанова задачі
2. Алгоритм розподілення продукції
3. Тренінг на оптимальність методів
4. Метод потенціалів перевірки оптимальності витрат
5. Перерозподілення продукції для отримання менших витрат
6. Переваги та недоліки

 

                                                           Лекція.

5.1  Постановка задачі.

Викладач знайомить студентів під запис в конспектах. Розв’язати транспортну задачу. Маємо 3 пункти виробництва і 3 пункти споживачів продукції. В 1 пункті виробляється 20т продукції, в 2-ому – 15т, в 3-ому – 25т. В 1-ий пункт споживання продукції необхідно 25т, в 2-ий – 10т. В 3-ий – 25т. Відомо про ціну перевезення однієї тони продукції з одного пункта виробництва в другий пункт споживання у вигляді матриці 3Х3:

 

3	2	4
2	1	5
3	4	2

 

   Знайти такий план перевезень продукціїї, щоб витрати на перевезення були мінімальними.

 

5. 2 Алгоритм розподілення продукції.

Викладач оголошує алгоритм, студенти конспектують, використовуючи роздатковий матеріал. При цьому викладач активізує розумову діяльність на підставі знань з дисципліни: «Вища математика» стосовно рівнянь і нерівнянь, які студентам потрібно використовувати під час виконання курсових проектів з дисципліни: «Об’єктно-орієнтоване програмування».

 

Крок 1. Складаємо транспорту таблицю на підставі даних транспортної задачі:

 

ai    /       bj	25	10	25
20	3	2	4
15	2	1	5
25	3	4	2

 

Крок 2. Перевіряємо, чи можна розв’язати транспортну задачу. Чи є ця транспортна задача  задачею закритого типу? Щоб можна було вирішити транспортну задачу необхідно, щоб  a_i   > =  b_j, а задача закритого типу, це коли  a_i    =  b_j. В нашому випадку  a_i    = 20+15+25=60, а  b_j=25+10+25=60, тобто маємо транспортну задачу закритого типу, яку можна вирішити.

 

Крок 3. Розподіляють кількість продукції методом північно-західного куту (є ще метод мінімального елементу та угорський метод) таким чином в клітку з індексами 11 записуть найменше серед a₁ і b₁, в нашому випадку 20 і 25, найменше 20, тощо поки не буде розподілено усю продукціїю, при цьому рухаємося по клітках з лівого боку і зверу донизу. Якщо продукцію вже вибрано з виробника чи поставлено до споживача, то кількість зменшують на це число. Отримаємо таку таблицю:

 

ai    /       bj	25	10	25
20	20               3	2	4
15	2	10                  1	5                  5
25	5                3	4	20                 2

 

Крок 4. Знаходять витрати на перевезення продукції Z:

Z=20*3+10*1+5*5+5*3+20*2=60+10+25+15+40=150.

Тепер повертаємося до кроку 3 і розподілемо продукцію методом мінімального елементу, починаючи з клітки з меншою ціною. Така клітка з індексами 22, а далі аналогічно методу північно-західного куту. Маємо транспортну таблицю:

 

ai    /       bj	25	10	25
20	20               3	2	4
15	5                 2	10                  1	5
25	3	4	25               2

 

і підрахуємо витрати: Z=20*3+5*2+10*1+25*2=60+10+10+50=130, тобто витрати менше, ніж в попередньому методі.

 

5.3 Тренінг на оптимальність методів.

    Викладач звертається до студентів з питанням тренінгу: «Чому витрати, які були отримані за домогою методу північно-західного куту становлять більше, ніж витрати, які були отримані за допомогою методу мінімального елементу». Студенти надають різні пропозиції, але вірним є те, що ми починаємо в другому методі з розподілення в клітку з мінімальною ціною. Але студентів під час тренінгу необхідно підвести до того, що існує ймовірність, коли в одному методі може скластися таке розподілення, що може бути більш оптимальним, ніж в інших.

 

5.4     Метод потенціалів перевірки оптимальності витрат.

Якщо метод мінімального елементу надав менші витрати, то ми їх перевіримо на оптимальність. Чи є дане розподілення найоптимальнішим. Введемо потенціали u_i і v_j . Складемо суму потенціалів для заповнених кліток, яка дорівнює ціні. Для того, щоб можна було розв’язати за допомогою метода потенціалів задачу, необхідно мати заповнених кліток m+n-1, де m-кількість строк, а n-кількість стовпчиків. У нашому випадку 3+3-1=5, а маємо 4 заповнених клітки, тому в клітку з індексами 13 запишемо 0, отримаємо таблицю:

 

ai    /       bj	25	10	25
20	20               3	2	0                 4
15	5                 2	10                  1	5
25	3	4	25               2

 

Складаємо суму потенціалів:

U1+V1=3

U1+V3=4

U2+V1=2

U2+V2=1

U3+V3=2,

нехай U1=0, тоді V1=3, V3=4, U2= -1, V2=2, U3= -2.

В незаповнених клітках повина виконуватися умова U_i+V_j <=C_ij, де C_ij – ціна перевезення. Тоді розподілення буде оптимальним (мінімальним).

 

ui    /       vj	3	2	4
0	20               3	2	0                 4
-1	5                 2	10                  1	5
-2	3	4	25               2

 

В незаповнених клітках винується умова U_i+V_j <=C_ij, тому дане розподілення оптимальне, а витрати Z=130 – мінімальні.

 

5.5 Перерозподіл продукції для отримання менших витрат.

Викладач активізує розумову діяльність студентів на базі вивченої дисципліни «Числові методи». Треба визначитися від чого залежить точність вирішення. Чим більше ітерації, тим краще точність розрахунків. Щось подібне і в нашому випадку: метод північно-західного куту легше, не треба перебирати усі клітки, щоб розшукати з меншою ціною, розподілення робиться підряд, але ми отримали неоптимальні витрати, як під час методу мінімального елементу. Далі викладач коментує розробку програм за допомогою мов програмування Borland Pascal (студенти вивчали в попередньому семестрі) та Borland C++ (студенти вивчають в поточному семестрі) і системи проектування  Borland Delphi (студенти будуть вивчати на наступному курсі): обов’язково треба враховувати точність.

А далі про саме перерозподілення. В нашому випадку у всіх клітках, які не були заповнені, виконувалася умова U_i+V_j <=C_ij, а якби в якійсь клітці не виконувалася дана умова, то в цю клітину необхідно робити перезподілення продукції, далі зв’язати її з клітками, де вже є розподілення, проставити в клітку “+”, тобто додавати і в черзі проставити “-“, “+”, “-“, там де “-” – це означає віднімати. Обрати найменше число в клітинах і далі там, де “+” додати це число, де “-” зменшити на це число. Потім через метод потенціалів перевірити перерозподілений план.

 

5.6 Переваги та недоліки.

Переваги:

•                Для розподілу продукції не треба вираховувати як краще перевезти продукцію між споживачами. Треба тільки використовувати алгоритм і можна отримати оптимальне рішення.
•                Не існує ніяких обмежень для методів: північно-хахідного кутк, мінімального елементу, потенціалів (крім  a_i   > =  b_j).
•                Швидше розв’язання задачі.
•                Кількість пунктів споживачів і виробників не обмежена.

Недоліки:

•                Не можливо вирішити задачу, коли  a_i   <  b_j
•                Можливе зацілення при розподілі, коли не існує вирішення більш оптимального.

 

6. Закріплення навчального матеріалу.

6. 1  Фронтальне опитування. Викладач проводить опитування за алгоритмом методу, особливостями, різновидами, де можна використовувати (додаток Б).     До 5 хвилин.
   2.                    Розв’язання задачі. Викладач надає студентам завдання тільки на розподіл продукції (до 5 хвилин):

 

ai    /       bj	5	10	5
5	1	3	2
5	5	2	5
10	1	4	1

 

Викладач в цей час перевіряє письмові роботи і працює зі студентами, яким не вдається розв’язати задачу.

6.3 Тренінг на закріплення нового матеріалу. Студентів, які швидко вирішили задачу, викладач розподіляє на 2 групи. Одна група буде через тренінг доводити, що транспортну задачу можна використовувати на виробництві, а інша, що ні   (до 5 хвилин).

 

7   Підсумок заняття.  

Викладач підводить підсумки (до 2 хвилин) щодо виконання студентами завдань та досягнення мети заняття, коментує та вмотивовує оцінки. Для студентів, які не зовсім розібралися з методом, викладач нагадує, що є можливість скористатися елементами дистанційного навчання через глобальну світову мережу Інтернет, а саме звернутися із запитаннями до електронної скриньки: e-mail mmmk-zo@yandex.ru. Викладач дякує за активну участь у занятті.

9.   Домашнє завдання (до 2 хвилин).
   1.   Опрацювати  літературу: Бугір М.К. Математика для програмістів        

§9.12 – 9.14 та конспект

2. Підготуватися до тестування за темою «Транспортна задача»

      9.3  Самостійно розв’язати задачі за варіантами з контрольної роботи.

 

 

                                                      Висновки.

 

        Тренінги сприяють розвитку продуктивного творчого мислення студентів через інтуїтивне мислення, «догадки», які супроводжуються станом      «освітлення», дією логіки. Тренінги необхідні для колективного вирішення спеціально сформульованих проблемних ситуативних задач. При цьому складається фонд ідей з конкретної проблемної ситуації. Студенти колективно генерують ідеї. Викладач при цьому виступає як диригент. Він заперечує критику ідей, заохочує нетрадиційні висловлювання, допомагає розвитку ідей, але не дає якісної оцінки відповідей і приймає кожний доказ як можливий. Тут одразу можна зазначити, що головною ідею тренінгу є навчання студента нетрадиційно мислити. Цьому допомагає те, що студенти мають невеликий досвід, і в цьому сенсі, вони відносно не «зашорені», не стереотипні і відкриті.

        Тренінги допомагають реалізувати передачу знань між студентами, розвивають  навички та вміння, надають умови для саморозкриття студентів і самостійного пошуку ними вирішення особистих проблем.       

         І головне, під час тренінгу чи дебатів викладач ні в якій мірі не повинен втручатися в обговорення групи, а лише спрямовувати в потрібному напрямку.

          Під час тренінгу необхідно створити неформальне, невимушене спілкування учасників тренінгу, яке відкриває групі безліч варіантів розв’язання проблеми, сприяє розвитку групової динаміки, міжособистісних взаємин і норм у групі, заради якої вона зібралася або була сформована. Як правило, учасники в захваті від тренінгових занять, тому що ці методи роблять процес пізнання цікавим та не обтяжливим.

    Тренінг, перш за все, орієнтований на запитання та пошук. На відміну від традиційних, тренінгові форми навчання ініціалізують весь потенціал людини: рівень та обсяг її видів компетентностей, які мають місце в професійній діяльності, самостійність, здатність до прийняття рішень, до взаємодії тощо.

    Тренінг як і будь-яка інша організаційна форма навчання, підпорядкований певній меті.

    Головне, що забезпечує сприятливу атмосферу для навчання у тренінговій групі, - це правила, яких має дотримуватися кожний учасник. Основні з них: цінування часу, увічливість, позитивність, розмова від свого імені, «додавання», добровільна активність, конфіденційність, «стоп», «піднята рука», зворотний зв’язок.

Тренінг проводить тренер (ведучий), котрий спілкується з учасниками «на рівних», тобто є таким самим учасником тренінгової групи, як і інші учасники. Тренер одночасно є й каталізатором усіх процесів, які відбуваються в групі, «керманичем» групи на шляху до досягнення визначеної мети тренінгу та повинен розуміти настрій кожного учасника та відрізняється від інших учасників тим, що:

• володіє інформацією щодо означеної теми;
• знає методику проведення тренінгових занять;
• вміє працювати з аудиторією і володіє методикою навчання дорослих і дітей;
• володіє навичками ведення тренінгової групи (регулює групові процеси, знає, як зацікавити учасників, зняти напруження, спрямувати групу на конструктивне розв’язання проблеми тощо);
• постійно підвищує свій тренерський потенціал;
• знає методи оцінювання результатів тренінгу і вміє їх застосовувати;
• знає про відстрочені результати впливу тренінгу, як очікувані, так і неочікувані.

Тренінг сприяє інтенсивності навчання, результат якого досягається завдяки власній активній роботі його учасників. Знання під час тренінгу не подаються в готовому вигляді, а стають продуктом активної діяльності самих учасників. У центрі уваги - самостійне навчання учасників та інтенсивна їх взаємодія. Відповідальність за результативність тренінгового процесу несуть однаковою мірою як ведучий, так і кожний учасник тренінгу

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

                                          Література.

 

1     Бугір М.К. Математика для програмістів, підручник , К: 2003

2     Єрмаков І.І.  Довідник з математики для економістів, К: 1998

3     Руденко В.Д.  Курс інформатики, підручник, К: 2004

4     Симонович А.І. Комп’ютерна техніка, М: 2001

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

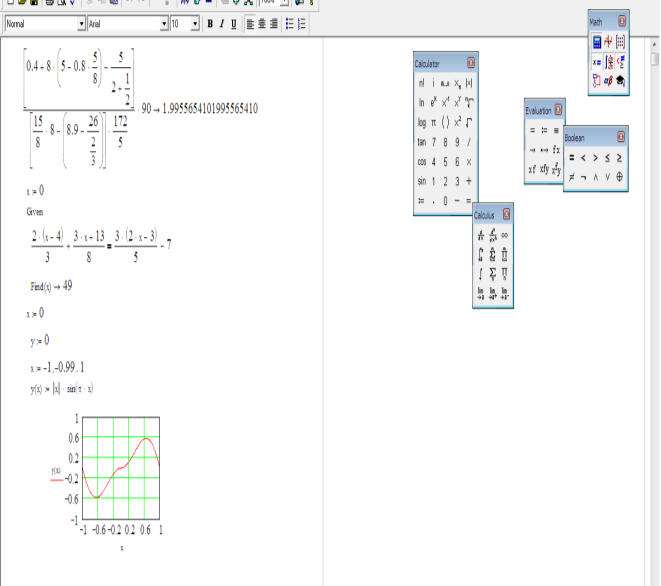
Додаток А

 

Приклад вирішення за допомогою MathCAD.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Додаток Б

 

Питання  фронтального опитування .

 

1   В яких випадках не можливо вирішити транспортну задачу?

2   Що записують в клітини транспортної таблиці?

3   Що необхідно зробити для того, щоб виконувалось рівняння Σa_i=Σb_j ?

4   Які методи розподілення вантажів Ви знаєте ?

5   Як порахувати суму перевезення вантажу ?

6   Що означає u_i+v_j=c_ij ?

7   Для чого використовується метод потенціалів ?

8   Яка умова виконується в незаповнених клітинах ?

9   Скільки заповнених клітин необхідно мати для того, щоб можна було

     використовувати метод потенціалів ?

10 Як виконується перерозподілення вантажу ?