Малювати, щоб думати…

 

 

 

 

Застосування кіл Ейлера у математиці.

 

 

 

 

Зміст

Вступ

1.   Історична довідка. Кола Ейлера.

1.1.   Біографія Леонарда Ейлера.

1.2.   Внесок у науку.

1.3.   Кола Ейлера.

1.4.   Типи кіл Ейлера.

2.   Розв’язування задач за допомогою кіл Ейлера.

2.1.   Алгоритм рішення завдань за допомогою кіл Ейлера

2.2.   Застосування кіл Ейлера у роботі із дошкільнятами.

2.3.   Застосування кіл Ейлера у роботі із НУШ.

2.4.   Застосування кіл Ейлера у роботі із старшокласниками.

2.4.1.   Розв’язування задач арифметичним способом.

2.4.2.   Розв’язування задач алгебраїчним способом.

3.   Задачі для самостійного опрацювання.

Висновок.

Список джерел і літератури.

 

 

 

 

 

 

 

 

 

 

 

 

 

Вступ.

Навчально-методичний посібник розрахований для учнів та вчителів математики загальноосвітніх навчальних закладів.

Розв’язання будь-якої задачі тією чи іншою мірою базується на проведенні певних роздумів. Існують задачі, які можна розв’язати майже без обчислень. Для цього потрібно тільки послідовні (логічні) міркування, бажання, наполегливість, кмітливість і терпіння.

У шкільному курсі математики особливе місце посідають завдання логічного характеру. Такі задачі приваблюють учнів, своїм життєвим спрямуванням, нестандартним цікавим формулюванням умови, що сприяє формування у нас зацікавленості до предмету математики. Розв’язування задач такого змісту вчить аналізувати, порівнювати, робити висновки, а іноді й шукати нестандартні способи розв’язування. Такі вміння допоможуть учням у майбутньому не лише оволодіти математикою чи іншою наукою, а ще й в житті не ховатися від проблем (якщо розглядати їх як життєві задачі та шукати шляхи вирішення).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1.                Історична довідка. Круги Ейлера.

 

1.1. Біографія Леонарда Ейлера.

 

Ейлер народився 15 квітня 1707 р. в м Базель, в Швейцарії. В маленькій тихій Швейцарії, куди із всієї Європи

приїжджали митці          і         науковці. Незабаром після народження сина, родина переїжджає в містечко Рієн. Батько хлопчика був другом Йоганна Бернуллі – відомого європейського математика, що зробив великий вплив на Леонарда. У тринадцять років Ейлер-молодший вступає до Базельського університету, і в 1723 р отримує ступінь магістра філософії. У своїй дисертації Ейлер порівнює філософії Ньютона і Декарта. Йоганн Бернуллі, що давав хлопчикові по суботах приватні уроки, швидко розпізнає видатні здібності хлопчика до математики і переконує його залишити ранню теологію і зосередитися на математиці.

У 1727 р Ейлер бере участь в конкурсі, організованому Паризькою академією наук, на кращу техніку установки корабельних щогл. Леонард займає друге місце, в той час як перше дістається П’єру Бугеру, який згодом стане відомий як «батько кораблебудування». Ейлер щороку бере участь в цьому конкурсі, отримавши за своє життя дванадцять цих престижних нагород.

17      травня 1727 р. Ейлер надходить на службу до медичного відділення Імператорської російської академії наук в Санкт – Петербурзі, але майже відразу ж переходить на математичний факультет та 19 червня 1741 р Ейлер переводиться в Берлінську академію. Там учений прослужить близько 25 років, написавши за цей час понад 380 наукових статей. У 1755 р. його обирають іноземним членом Шведської королівської академії наук.

На початку 1760-х рр. Ейлеру надходить пропозиція навчати наукам принцесу Ангальт-Дессау, якій вчений напише більше 200 листів, які увійшли в популярний збірник «Листи Ейлера на різні предмети натуральної філософії, адресовані німецькій принцесі». Книга не тільки наочно демонструє здатності вченого міркувати на всілякі теми в області математики і фізики, але також є виразом його особистих і релігійних поглядів. Цікаво те, що ця книга відома краще, ніж всі його математичні праці. 

18      вересня 1783 року він помирає.

На згадку про його величезний внесок у науку, портрет Ейлера з’явився на швейцарських 10 – франкових банкнотах шостої серії, а також на ряді російських, швейцарських і німецьких марок.

 

1.2. Внесок у науку.

 

Система математичних позначень

Серед всіх різноманітних робіт Ейлера найпомітнішою є уявлення теорії функцій. Він першим ввів позначення f (x) – функції “f” по аргументу “x”. Ейлер також визначив математичні позначення для тригонометричних функцій в тому вигляді , в якому ми знаємо їх зараз , ввів літеру “e” для заснування натурального логарифма (відому як «число Ейлера»), грецьку букву “Σ” Для підсумкової суми і букву “і” для визначення уявної одиниці.

Аналіз

Ейлер затвердив застосування показникової функції і логарифмів в аналітичних доказах. Він відкрив спосіб розкладання різних логарифмічних функцій в степеневий ряд, а також успішно довів застосування логарифмів до негативних і комплексних числел. Таким чином, Ейлер значно розширив математичне застосування логарифмів.

Цей великий математик також докладно пояснив теорію вищих трансцендентних функцій і представив новаторський підхід до вирішення квадратних рівнянь. Він відкрив техніку розрахунку інтегралів із застосуванням складних меж. Розробив він і формулу варіаційного обчислення, що отримала назву «рівняння Ейлера – Лагранжа».

Теорія чисел

Ейлер довів малу теорему Ферма, тотожності Ньютона, теорему Ферма про суми двох квадратів, а також значно просунув доказ теореми Лагранжа про суму чотирьох квадратів.

Помітний внесок вніс Ейлер в рішення рівняння пучка ЕйлераБернуллі, яке стало одним з основних рівнянь, застосовуваних в інженерній справі. Свої аналітичні методи вчений застосовував не тільки в класичній механіці, але і в рішенні небесних завдань. За свої досягнення в області астрономії Ейлер отримав численні нагороди Паризької академії. Грунтуючись на знанні істинної природи комет і розрахувавши паралакс Сонця, вчений чітко обчислив орбіти комет та інших небесних тіл. За допомогою цих розрахунків були складені точні таблиці небесних координат.

 

1.3. Круги Ейлера.

 

Круги Ейлера – це геометрична схема, про перетин взаємодоповнюючих і взаємовиключних факторів, які схематично зображуються у вигляді кіл. З їх допомогою можна зобразити відносини між підмножинами (поняттями), для наочного представлення. Метод Ейлера є незамінним при вирішенні деяких завдань, а також спрощує розмірковування.

Леонард Ейлер був геніальним математиком, який умів застосовувати математичні прийоми на практиці. Він успішно використав для вирішення різних завдань ідею зображення понять і класів предметів у вигляді кіл. З допомогою цих графіків можна легко і наочно розв’язати завдання з громіздкими умовами, для вирішення яких звичайним способом знадобилося б складання системи з декількох рівнянь, наприклад, з трьома невідомими. Подібні завдання часто мають практичний характер, що важливо в сучасному житті. Вони змушують замислюватися, підходити до вирішення будь-якої проблеми з різних сторін, вміти вибирати з безлічі способів вирішення найбільш простий, легкий шлях.  

 

1.4.Типи кругів Ейлера

 

Круги Ейлера — це шість простих геометричних схем, які допомагають розібратися у співвідношенні понять. Математик Леонард Ейлер придумав їх ще у XVIII столітті та припустив, що цей інструмент спростить роздуми кожному, хто мислить.

Ейлер   запропонував       шість          типів відносин:    рівнозначність, підпорядкування,      співпідпорядкування,    перетин,      суперечності, протилежності. Ось як вони пояснюються за допомогою кіл:

 

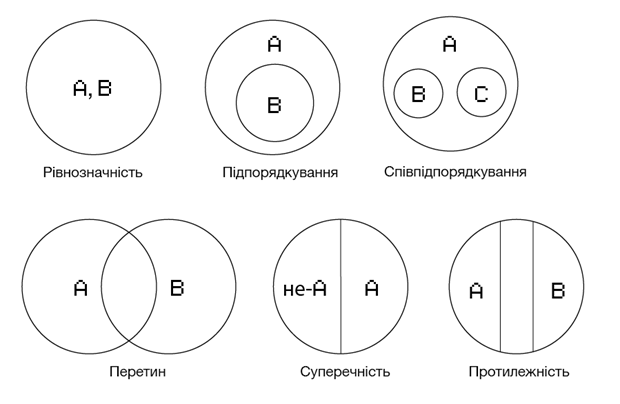
По суті, кола Ейлера — спосіб візуалізувати відносини між будь-якими об'єктами, групами об'єктів та навіть абстрактними поняттями. 

Чим більше понять, тим складніше уявити їхні зв'язки подумки, цифрами, списками — і тим ефективніше робити схему. 

Найбільш надійний спосіб розібратися в механізмі системи, яку придумав Ейлер, знайти приклади в готових кейсах. Побачиш, як працює рівнозначність у стратегії бренду чи перетин у пошуках героя для рекламного ролика — зрозумієш, як використати цей підхід для своїх цілей.

1.           Рівнозначність Ейлера цей тип взаємодії понять виглядає як два кола, що повністю збігаються. Одне дорівнює іншому, як їх не назви. 

2.           Підпорядкування. 

Допустимо, загальне поняття — це велике коло. Всередині нього розташоване інше, маленьке, і воно — частина великого. 

3. Співпідпорядкування

Графічний ключ до цього співвідношення — велике коло, всередині якого містяться декілька маленьких. Маленькі поняття між собою на рівних і повністю включені до чогось загального

Якщо помістиш ключове поняття в не дуже очевидну сферу і шукатимеш підпорядкування в ній, вийде крутий експірієнс. Наприклад, очевидно було з початком пандемії знаходити паралелі у минулому, зокрема, з епідемією «іспанки».

4. Перетин

Ця діаграма Ейлера — найбільш культова і попсова, особливо в економіці. Суть у тому, що обсяг одного поняття частково збігається з обсягом іншого — вони мають щось спільне.

5. Суперечність

На відміну від протилежності, суперечність тримається на конфлікті. Коло розділене навпіл. Одна його частина стверджує, що не є другою. І навпаки.

6. Протилежність

Поняття з протилежними характеристиками Ейлер представляє як дві частини кола, між якими залишається вільний простір — це все інше.

Протилежності — це мирні антоніми, які не вступають у конфлікт і не будують своєї ідентичності на запереченні одне одного. Наприклад це холодне, а це гаряче. 

Отже, у системі Ейлера — шість простих геометричних схем, які може намалювати від руки навіть дитина. Окремо кожна з них визначає лише одну взаємодію. Але якщо берешся за велику тему, в твоїй схемі можуть поєднуватись одразу декілька типів співвідношень.

Тестувати світ на суперечності та зв'язки — суперкорисно та суперзахопливо. Хороші новини: ти не зможеш зупинитись. Погані новини: ти не зможеш зупинитись.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2. Розв’язування задач за допомогою кіл Ейлера

 

2.1.Алгоритм рішення завдань за допомогою кіл Ейлера

 

Спосіб зображення понять у вигляді кіл дозволяє розвивати уяву і логічне мислення не тільки дітям, але і дорослим (звичайно, для дорослих підійдуть більш складні завдання). Починаючи з 4-5 років дітям доступно рішення найпростіших завдань з колами Ейлера, спочатку з роз’ясненнями дорослих, а потім і самостійно. Оволодіння методом вирішення завдань з допомогою кіл Ейлера формує в учнів здатність аналізувати, зіставляти, узагальнювати та об’єднувати свої знання для більш широкого застосування.

Алгоритм рішення завдань за допомогою кіл Ейлера :

1.   Уважно вивчаємо і коротко записуємо умову завдання. 

2.   Визначаємо кількість множин і позначаємо їх. 

3.   Виконуємо малюнок. Будуємо перетин множин. 

4.   Записуємо початкові дані в круги.

5.   Вибираємо умову, в якій міститься більше властивостей. 

6.   Записуємо дані, яких не вистачає в колах Ейлера (міркуючи і аналізуючи) 

7.   Перевіряємо рішення задачі і записуємо відповідь.

Розглянемо цей алгоритм при розв’язанні задач

 

2.2. Застосування кіл Ейлера у роботі із дошкільнятами.

 

У математиці рисунки у вигляді кіл, які зображають множини, використовують давно. 

Як фігури найчастіше використовують кола, але можна також розглядати квадрати, прямокутники й інші фігури. Сам Ейлер, зазначав, що «вони підходять для  того, щоб  полегшити наші  міркування».

Із дошкільниками їх використовують також і це допомагає розвивати увагу, логічне мислення. А логічне мислення – це мистецтво міркування. А при міркуванні ми розвиваємо мовлення: чому саме так треба розмістити предмети, а не інакше. Насамперед ми вчимося класифікувати предмети за певними ознаками. Якщо логічне мислення, та ще й уява добре розвинені у людини, то вона здатна творчо мислити і творчо підходити до поставлених завдань. Розвитку логічного мислення необхідно вчитися. Потрібно вміти користуватися логічним мисленням і уявою. Потрібно також розвивати і всіляко сприяти розвитку логічного мислення. Адже це знадобиться в житті! Для ефективного розвитку логічного мислення можна і потрібно вирішувати різні ситуаційні задачі і загадки. Як стандартні логічні завдання головоломки, так і нестандартні. Це одночасно розвиває логіку, інтелект, уяву, фантазію. Багато ігор, завдань і головоломок розвивають логічне мислення. До них можна віднести кола Ейлера. 

 Круги (кола) Ейлера можна використовувати не тільки на заняттях з математики, але і на інших заняттях. 

 

Завдання:  Логічні вправи з наліпками. 

 

1.           Розмісти   всередині    круга 

фрукти. Ззовні круга – овочі.

 

 

      

  

  

  

  

2.           Розмістити іграшки так, щоб

в жовтому      колі   опинились іграшки,       якими         граються дівчатка, а в синьому хлопчики.

 

3.В жовтому колі розмістити транспорт, а в синьому – спецтранспорт.  

 

 

Жовтий круг	Синій круг
Всі квадратні фігури	Всі зелені фігури
Всі жовті фігури	Всі         трикутні фігури
Всі маленькі фігури	Всі круглі фігури

4Розкласти геометричні фігури так, щоб всередині жовтого круга були всі червоні фігури, а всередині силього – всі круглі.

 

 

Отже, спосіб зображення понять у вигляді кругів дозволяє розвивати уяву і логічне мислення. Оволодіння методом рішення завдань за допомогою кругів Ейлера формує у дитини здатність аналізувати, зіставляти, узагальнювати і групувати свої знання для ширшого застосування.

 

2.3. Застосування кругів Ейлера у роботі з НУШ.

 

Для дітей початкової школи можна пропонувати варіанти завдань з обчисленнями — від досить простих до зовсім складних. Причому самостійне вигадування цих завдань для дітей забезпечить дуже хорошу розминку для розуму. 

 

1. Об'єднайте у групи за певними  ознаками. (Інакше ці групи можна  назвати множинами. Множина—це 

сукупність

об'єднуються за певною спільною ознакою).

 

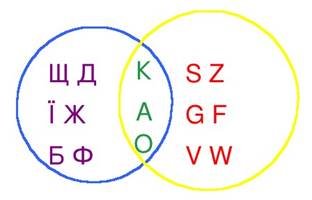2.

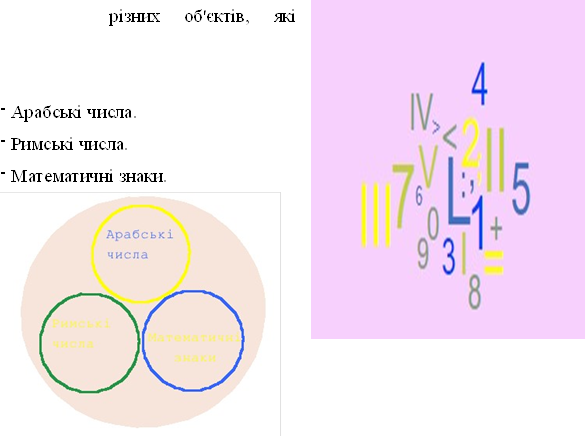
-     Що спільного між об’єктами,

          обведеними     жовтою     лінією?

(Букви українського алфавіту.) - Що спільного між об'єктами,

          обведеними     синьою     лінією?

(Букви англійського алфавіту.)  

-     Що утворилося на перетині множин? (Букви, спільні для

обох алфавітів.)

 

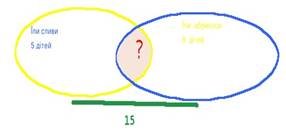3. На галявині сиділо 15 дітей. П'ятеро з них їли сливи, восьмеро — абрикоси. Фруктами смакували усі. Скільки дітей їли і сливи, і абрикоси?

 

(5 + 8 = 13 дітей, що їли або сливи або абрикоси. 15 - 13 = 2 дітей, які скуштували і сливи, і абрикоси.)

 

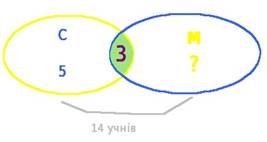4. У класі навчається 14 учнів. П'ять із них відвідують лише гурток спортивний, а три — і гурток спортивний, і гурток

          музичний.        Скільки         учнів  

відвідують     лише гурток музичний? (5 + 3 = 8 учнів, які відвідували гурток спортивний. 14 - 8 = 6 учнів, які відвідували лише гурток музичний.) 

2.4. Застосування кругів Ейлера у роботі із старшокласниками.

 

2.4.1. Розв’язування задач арифметичним способом. 

 

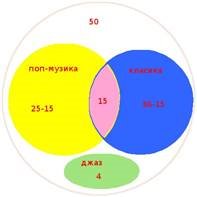Задача 1. Провели опитування  50 учнів ліцею із них 25 слухають поп-музику, 36 —

класику, а 15 — і класику, і поп-музику, а інші слухають джаз. Скільки школярів захоплюються джазом?

ПМ – 25 учнів слухають поп-музику;

К – 36 учнів слухають класичну музику;

ПМ+К – 15 учнів слухають і класику і поп-музику; лише ПМ –   25-15=10 учнів; лише К -        36-15=21 учень;

усього слухають і класику і поп-музику  21+10+15=46 учнів; слухають джаз  50-46=4 учні.

Відповідь: 4 учні.

 

Задача 2 (Кенгуру-2017)

У гурті 30 дівчаток. 18 з них пили сік, 16 пили каву, а деякі не пили нічого. Тих, хто пив і сік, і каву, у 2 рази більше, ніж тих, хто нічого не пив. Скільки дівчаток пили і сік, і каву?

Розв’язання: Зобразимо умову задачі графічно діаграмою Ейлера-Венна:

30 - 16 = 14 (д.) – ті,що пили сік без кави;

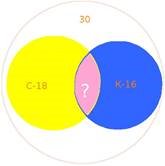30 - 18 = 12 (д.) – ті, що пили каву без соку; 14 + 12 = 26 (д.) – ті, що пили сік і каву разом;

30 - 26 = 4 (д.) – ті,що нічого не пили нічого; 4  2 = 8 (д.) – ті, що пили і сік, і каву. 

Відповідь: 8 дівчат пили і сік, і каву.

 

Задача 3

         Всі мої однокласники мають смартфони. Дев’ятнадцятеро  із них мають Xiaomi, двадцять один - Samsung. А у п’ятнадцяти однокласників є Xiaomi, і

Samsung. Угадайте, скільки учнів у моєму класі?

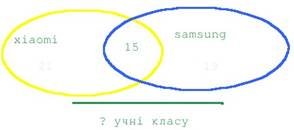      Розв’язання:

19 – 15 = 4 (у.) – мають лише Xiaomi;

21 – 15 = 6 (у.) – мають лише Samsung; 4+6+15 = 25(у.) – всього.

 

Відповідь: 25 учнів.                                      

 

Задача 4

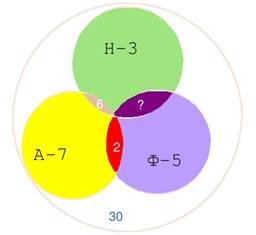        З 30 волонтерів семеро вивчали лише англійську мову, троє – тільки німецьку, п’ятеро  – тільки французьку. Четверо не вивчали   ніякі мови.          Шестеро      вивчав

англійську і німецьку, двоє – англійську і французьку. Скільки волонтерів вивчали німецьку і французьку мови?

      Розв’язання:  Зобразимо умову задачі графічно:

1)    30 – 4 = 26 (в.) – вивчають англійську, німецьку і французьку разом;

2)    7 + 6+ 2 = 15 (в.) – вивчають англійську;

3)    26 – 15 =11 (в.) – вивчають французьку разом з німецькою, але не вивчають англійську;

4)    11 – (3 + 5) = 3 (л.)  - вивчають і французьку, і німецьку.

Відповідь: 3 волонтери.

 

 

 

2.4.2. Розв’язування задач алгебраїчним способом

 

Задача 1

На уроці математики шестикласникам було задано розв’язати рівняння, спростити вираз  та обчислити приклад. Із 30 учнів класу троє правильно розв’язали лише рівняння, шестеро правильно лише спростили вираз, четверо правильно лише обчислили приклад. Не розв’язали тільки рівняння – 5 учні, не обчислили тільки приклад – 6 учнів, не спростили тільки вираз – 3 учні. Решта дітей виконали всю роботу. Скільки дітей на відмінно справились із завданнями?

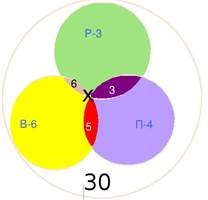Розв’язання: Зобразимо діаграму Ейлера-

Венна відповідно до умови задачі:  всього 24 учні;

Р- розв’язали лише рівняння; їх 2;

В - розв’язали лише вираз; їх 5; 

П – розв’язали лише приклад; їх 3;

Р + В – учні, які не обчислили тільки приклад; їх 5;

Р + Н – учні, які не спростили тільки вираз; їх 2;

В + Н – учні, які не розв’язали  тільки рівняння; їх 4;

Р+ Г + Н – це решта учнів, які розв’язали всі три завдання, їх позначимо х.

Складаємо   рівняння:

х + 6 + 3 + 5 + 3 + 6 + 4= 30; х + 27=30; х = 3.

Відповідь: 3 учнів класу справились на відмінно.  

 

Задача 2

Із 29 учнів класу на дистанційному навчанні 20 користуються ноутбуком (Н), 15 – планшетом (П), 23 – смартфоном (С). Ноутбук і смартфон використовують 10 учнів. Ноутбук і планшет – 12, а смартфон і планшет – 9.

Скільки учнів користуються трьома видами гаджетів?

Розв’язання: Зобразимо умову задачі за допомогою кіл Ейлера.

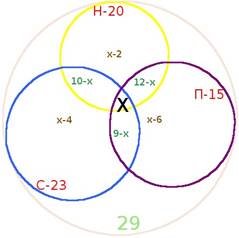Позначимо учнів, які користуються трьома видами гаджетів – х.  

Тоді позначимо:

Н - 20 учнів; 

П – 15 учнів;  С – 23 учня; лише Н+П  –  (12 – х);  лише П+С - (9 – х );  лише Н+С - (10 - х); лише Н -    20 – (12 – х +10 – х + х) = 20 – 12 + х - 10 + х – х = х – 2; лише П -   15 – (12 – х + 9 – х + х) = 15 – 12 + х –  9 + х –  х = х – 6 ; лише С -    23 – (10 – х + 9 – х + х)  = 23 – 10 + х – 9 + х –  х  = х + 4;

Складаємо рівняння:

(х – 2) + (х – 6) + (х + 4) + (12 – х) +( 9 –х) + (10 – х) + х = 29; х + 27 = 29; х = 2.

Відповідь: 3 учні .

 

Задача 3

 У класі двадцять два учні. З них десятеро захоплюються математикою, одинадцять – фізкультурою, дванадцять – інформатикою. Захоплюються тільки двома предметами – математикою і фізкультурою – двоє, математикою і інформатикою – четверо, фізкультурою і інформатикою  – шестеро. Троє не захоплюються ні математикою, ні фізкультурою, ні історією. 

1)    Скільки учнів одночасно захоплюються трьома предметами?

2)    Скільки всього учнів захоплюються лише одним із цих предметів?

Розв’язання:  Зобразимо умову задачі за допомогою кіл Ейлера.

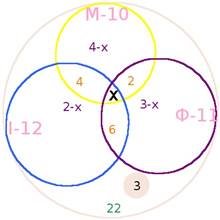Позначимо учнів, які захоплюються  трьома предметами   Тоді згідно цього матимемо позначення.

Кількість учнів, які захоплюються хоча б одним предметом: 22 – 3 = 19;

Захоплюються:

М – 10 учнів;

Ф – 11 учнів;

І – 12 учнів;

М+І – 4 учні;

М+Ф – 2 учні; І+Ф – 6 учнів;

лише М -     10 – (4 +2 +х) = 10 – 4  – 2 – х  = 4 – х; лише Ф -     11 – (2 + 6 + х) = 11 – 2 – 6 – х  = 3 – х; лише І -       12 – (6 + 4+х) = 12 – 6 – 4 – х  = 2 – х;

Складемо відповідне рівняння:

(4 – х) + (3 – х) + (2 – х)+ 4 + 2 +  6 +х = 19;

21 – 2х= 19; 2х = 2; х = 1 

лише М  -        4-1=3; лише Ф -         3-1=2; лише І   -         2-1=1;

Отже, 3+2+1=6 – всього учнів, які захоплюються лише одним із предметів.

Відповідь: 1) 1 учень ; 2) 6 учнів.

 

Задача №4

Із 36 хлопців  у баскетбол грають 12 , у футбол – 22, у волейбол – 14. Баскетболом і футболом займаються 5 з них, баскетболом і волейболом – 2, волейболом і футболом –6. Ніяким видом з цих видів спорту не займаються 3 з них.

1)    Скільки чоловік займаються трьома видами спорту одночасно?

2)    Скільки чоловік займаються лише в одній спортивній секції?

Розв’язання: Зобразимо умову задачі за допомогою кіл Ейлера.

Позначимо хлопців, які займаються трьома видами спорту – х. Тоді згідно цього матимемо позначення.

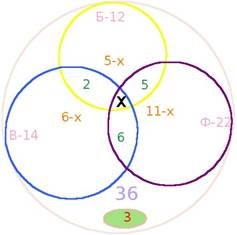Учні, які захоплюються хоча б одним видом спорту: 36 – 3 = 33;

Захоплюються:

Б -12  хлопців;

Ф -22 хлопців;

В – 14 хлопців;

Б+Ф – 5 хлопців;

Б+В – 2 хлопців; Ф+В - 6 хлопців ; лише Б -       12 – (2 + 5+ х) = 12 – 2  – 5 – х  = 5 – х; лише Ф -       22 – (6 + 5 + х) = 22 – 6 – 5 – х  = 11 – х; лише В -        14 – (2 + 6+ х) = 14 – 2 – 6 –х  = 6 – х;

Складемо відповідне рівняння:

5 - х + 11 - х + 6- х + 2 + 5 +  6 + х = 33;

35 – 2х = 33;

2х = 35 – 33; 2х = 2; х = 1.

Отже, лише Б -      5-1=4; лише Ф -      11-1=10; лише В -    6-1=5;

Тоді:  4+10+5=19 – всього учнів, які захоплюються лише одним із предметів.

Відповідь:  1) 1 учень;  2) 19 учнів .

 

3. Задачі для самостійного опрацювання.

 

1.     35 учнів класу 12 брали участь у конкурсі декламаторів віршів, 10 — у конкурсі на найкращий малюнок, 4 брали участь в обох конкурсах. Скільки учнів не брали участі в конкурсах взагалі?

2.     У групі з 80 туристів, що приїхали на екскурсію у Львів, 52 хочуть піти до драмтеатру, 30 — до музею, 12 хочуть піти до драмтеатру та у музей, інші в драмтеатр та музей йти не хочуть. Скільки туристів не збираються до драмтеатру та музею?

3.     Підприємство купило комп'ютер, факс, сейф і телефон за 42 700 грн. Факс, сейф і телефон разом коштують 19 700 грн, комп'ютер, сейф і телефон — 40 700 грн, факс і сейф разом коштують 17 200 грн. Скільки коштують окремо комп'ютер, факс, сейф і телефон?

4.     Школа дала звіт: усього в школі 60 шестикласників, з них 37 відмінників з математики, 33 — з української мови і 42 — з фізкультури. При цьому в 21 особи «дванадцять» з математики та української мови, а у 23 — з математики і фізкультури, у 22 — з української мови і фізкультури. При цьому 20 осіб вчаться на «відмінно» з усіх трьох предметів. Чи правильний звіт школи?

5.     У 8 класі навчається 40 учнів. Кожний із них вивчає не менше однієї іноземної мови: англійську, німецьку, французьку. 34 учні вивчають хоча б одну із двох мов: англійську і німецьку. 25 учнів – хоча б одну із двох мов: німецьку і французьку. 6 учнів – тільки німецьку. Одночасно дві мови – англійську і німецьку – вивчають на 3 учні більше, ніж німецьку і  французьку мови. Скільки учнів вивчають кожну мову окремо і скільки вивчають одночасно кожні дві мови?

6.     У групі дитячого садочка 18 дітлахів. Кожен із них виступав на святі новорічної ялинки: співали й танцювали. Семеро дітей співали.

1)      Скільки дітей танцювали, якщо п’ятеро і співали, і танцювали? 

2)      Скільки дітей виступило лише з таночком?  

 

Висновок

 

Отже, тема даної роботи, без сумніву, розширює математичний кругозір учнів, збільшує арсенал засобів, що використовуються в рішенні різноманітних завдань. Оволодіння методом вирішення завдань з допомогою кіл Ейлера формує у дитини здатність аналізувати, зіставляти, узагальнювати та об’єднувати свої знання для ширшого застосування на практиці.

Кола Ейлера використовують для вирішення логічних завдань уже в середній школі. Але схеми універсальні — та справді стануть у нагоді будькому, хто розмірковує над чимось.

Матеріал даної роботи буде корисним та цікавим як вчителям так і  учням, оскільки ці знання допоможуть їм підвищити якість знань незвичним для них способом. 

Тож намалюй, роздрукуй, запам'ятай кола Ейлера і використовуй.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Література

 

1.   Апостолова Г.В. Логічними стежинками математики: 5-9-ті кл. / Г. В. Апостолова, О.П. Бакал. – 2-ге вид. – Київ: Генеза, 2016. С. 83-90

2.   Басанько А.М., Романенко А.О. За лаштунками підручника з математики. –

К.: Генеза, 2007. – 160 с.

3.   https://dovidka.biz.ua/leonard-eyler-biografiya/

4.   https://dovidka.biz.ua/leonard-eyler-biografiya

5.   https://skvot.io/uk/blog/v-krugah-eylera