Використання систем алгебраїчних рівнянь в різних галузях

Використання систем лінійних рівнянь у різних галузях

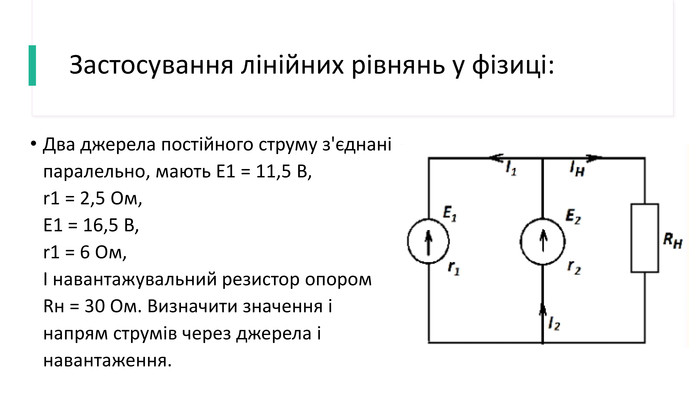
Застосування СЛАУ в задачі з економіки. Компанія випускає продукцію і продає її по 7 грн за одиницю. Керівництво компанії встановило, що сума загальних щотижневих витрат на виготовлення продукції в кількості Х має таку закономірність:𝒚𝑩=𝟏𝟎𝟎𝟎+𝟓𝒙Знайти точку рівноваги, області прибутків та збитків компанії. 

Розв’язання: Для рівноваги потрібно, щоб прибуток та витрати дорівнювали один одному, тоді зробимо рівняння:𝑦𝐷=7𝑥 – прибутки компанії (7 грн * одиницю)Отже, якщо 𝑦𝐵=𝑦𝐷 , то:𝟕𝒙=𝟓𝒙+𝟏𝟎𝟎𝟎𝟕𝒙−𝟓𝒙=𝟏𝟎𝟎𝟎𝟐𝒙=𝟏𝟎𝟎𝟎𝒙=𝟓𝟎𝟎 Таким чином з’ясували, що компанія має виробляти більше за 500 одиниць товару, щоб отримати прибутки.  

Застосування лінійних рівнянь у фізиці: Два джерела постійного струму з'єднані паралельно, мають E1 = 11,5 B,r1 = 2,5 Ом, E1 = 16,5 B, r1 = 6 Ом, І навантажувальний резистор опором Rн = 30 Ом. Визначити значення і напрям струмів через джерела і навантаження.

Розв’язання: Сформуємо систему рівнянь відповідно до правила Кірхгофа:𝐼1−𝐼2+𝐼𝑛=02.5𝐼1+6𝐼2=530𝐼𝑛+6𝐼2=16.5 𝐼1−𝐼2+𝐼𝑛=08.5𝐼1+6𝐼𝑛=56𝐼1+30𝐼𝑛=16.5 Отримуємо:𝐼1−𝐼2+𝐼𝑛=08.5𝐼1+6𝐼𝑛=5−45𝐼1=−13.5 𝐼1=−13,5−45=0,3 𝐼𝑛=5−8.5𝐼16=0.41 Звідси: 𝐼2=𝐼𝑛+𝐼1=0.71 

При розчиненні в кислоті 2,33 г суміші заліза і цинку отримано 896 мл водню (н.у.). Скільки грамів кожного металу містилося в суміші?СЛАР в хімії:

Розв’язання: Припустимо, що маса заліза в суміші дорівнює x г, тоді маса цинку дорівнює (2,33-x) г. Рівнянням встановлюємо пропорційну залежність між масою заліза і об'ємом виділився водню.m(Zn)= 2,33-xm(Fe)=1,68гm(Zn)=2,33г-1,68г=0,65г. Відповідь: 1.68г та 0.65г

Транспортна задача. З одного міста в інше треба перевезти обладнання трьох типів, для кожного 95, 100 та 185 одиниць відповідно. Кількість обладнання, котре вміститься в окремий вид транспорту задано на таблиці. Знайти скільки одиниць транспорту кожного виду потрібно, щоб перевезти це обладнання:

Розв’язання: Задамо цю задачу системою лінійних рівнянь, складемо матрицю та розв’яжемо її:3𝑥+2𝑦+𝑧=954𝑥+𝑦+2𝑧=1003𝑥+5𝑦+4𝑧=185 321412354 Розв’яжемо систему рівнянь методом Крамера.∆=-21 ∆х=-315 ∆у=-420 ∆z=-210 

Відповідь. X= 315 / 21 = 15 Y = 420 / 21 = 20 Z = 210 / 21 = 10 Отже, транспорту першого типу треба застосувати 15 одиниць, другого – 20, третього – 10.