Випадкова подія. Ймовірність випадкової події.

Тема уроку. Випадкова подія. Ймовірність випадкової події.

Мета уроку: домогтися засвоєння учнями змісту понять: випадкова подія, вірогідна подія, неможлива подія; означення ймовірності випадкової події; формули для обчислення ймовірності про­стої випадкової події. Виробити вміння: визначати вид події (випадкова, вірогідна, неможлива); визначати за формулою ймовірність простої події, а також розв'язувати задачі, що передбачають обчислення ймовірності за формулою.

Тип уроку: засвоєння знань, вироблення вмінь.

Наочність та обладнання: опорний конспект № 25.

Хід уроку

I. Організаційний етап

Учитель перевіряє готовність учнів до уроку, налаштовує їх на роботу.

II. Перевірка домашнього завдання

Учитель збирає зошити учнів із виконаною домашньою само­стійною роботою на перевірку. Для учнів, які потребують додат­кової педагогічної уваги, учитель заздалегідь готує розв'язання вправ самостійної роботи, які роздає учням для самостійного опра­цювання вдома.

III. Формулювання мети і завдань уроку.
Мотивація навчальної діяльності учнів

Учитель нагадує учням, що основна мета вивчення теми З «Елементи прикладної математики» — це оволодіння найпро­стішими способами розв'язування прикладних задач, а також способами оцінювання та подачі інформації про реальні фізичні, . соціальні та хімічні процеси. У цьому контексті стає зрозумілою логіка вивчення матеріалу даної теми. Після розгляду питання про загальний спосіб розв'язування прикладних задач вивчаються питання про окремі види прикладних задач, якщо розглядати їх з точки зору способу опису реальних процесів: задачі на відсотки описують зміну величин; задачі на ймовірність показують мож­ливість того, що відбудеться або не відбудеться певний процес, задачі на застосування елементів статистики вчать учнів подава­ти інформацію про результати процесів різними способами. Усі ці міркування вчитель подає учням в адаптованій формі, після чого формулюється мета даного уроку: повторити та систематизувати знання учнів про ймовірність випадкової події, отримані ними у 6 класі, а також доповнити їх знаннями про способи обчислен­ня ймовірності випадкової події.

IV. Актуалізація опорних знань та вмінь учнів

Усні вправи

1. Знайдіть:

1) 40% від числа 2,5;  2) 10% від числа 1,7;  3) 130% від числа 1.

2. Знайдіть:

1) число, 15% якого дорівнює 75; 

2) число, 80% якого дорівнює 4.

3. Знайдіть відсоткове відношення чисел:

1) 4 і 20;  2) 27 і 108.

4. Які події можуть відбутися внаслідок випробування:

1) підкидання грального кубика;

2) витягування кульки з ящика, у якому є білі та чорні кульки;

3) підкидання монети;

4) вибір деталей із партії, у якій 100 якісних деталей і 2 брако­вані?

V. Формування знань

План вивчення нового матеріалу

1. Уявлення про зміст понять: подія, випадкова подія, вірогідна подія, неможлива подія.
2. Класичне означення ймовірності випадкової події. Формула обчислення ймовірності випадкової події.

Опорний конспект № 25

Методичний коментар

Вивчення матеріалу уроку починається з формулювання уяв­лення учнів про зміст загального означення понять події, випадко­вої події, вірогідної події, неможливої події майже на побутовому рівні, тобто учні мають усвідомити, що являють собою такі види подій, не даючи їм математично строгих означень, а також на­вчитись наводити приклади таких видів подій.

Класичне означення ймовірності та формула обчислення ймо­вірності простих випадкових подій Р(А) = (див. опорний кон­спект № 25) також формулюються на інтуїтивному рівні, без стро­гих означень, і ґрунтуються на життєвому досвіді учнів. Проте на деяких математичних властивостях цього відношення слід на­голосити: ймовірність виражається невід'ємним числом у межах від 0 до 1, ймовірність неможливої події дорівнює 0, ймовірність вірогідної події дорівнює 1.

VI. Формування вмінь

Усні вправи

1. Які з наведених подій є випадковими:
   1. випадання герба при однократному підкиданні монети;
   2. виграш у лотерею 5 грн;
   3. випадання двох шісток на двох гральних кубиках при їх підкиданні;
   4. витягування чорної кульки з ящика, у якому всі кульки білі;
   5. витягування чорної кульки з ящика, у якому 10 чорних кульок.
2. Наведіть приклад:

1) вірогідної події; 2) неможливої події.

3. У ящику 12 білих, 7 чорних та одна зелена кулька. З нього навмання беруть одну кульку. Яка ймовірність того, що вона буде: 1) білою; 2) чорною; 3) зеленою?

Письмові вправи

Для реалізації дидактичної мети уроку слід розв'язати вправи такого змісту:

1. серед запропонованих прикладів подій назвати випадкові, ві­рогідні, неможливі;
2. знайти ймовірність випадкових подій за формулою;
3. на повторення: задачі на відсоткові розрахунки, задачі на скла­дання та розв'язування математичної моделі.

Методичний коментар

Для кращого засвоєння учнями матеріалу уроку рекоменду­ється при виконанні відповідних вправ неодноразово повторювати зміст вивчених понять. Важливо відпрацювати вміння виконувати дії, що передбачені застосуванням формули ймовірності: знайти кількість усіх можливих випадків; знайти кількість сприятливих випадків; знайти відношення кількості сприятливих випадків до кількості всіх можливих випадків. При цьому при підрахунку кількості як одних, так і інших варіантів випадків доречно вико­ристовувати як правила перебору варіантів, так і початкові відо­мості з комбінаторики, якщо учні володіють такими.

VII. Підсумки уроку

Контрольні запитання

1. Наведіть приклад:

1) випадкової події; 2) неможливої події; 3) вірогідної події.

2. Чи може ймовірність деякої події А дорівнювати:
   1)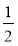 ;  2) 0;  3) -1;  4) 1;  5) 1,5?
3. У прогнозі погоди було сказано: наступного дня ймовірність опадів дорівнює 0,75. Що це означає?

VIII. Домашнє завдання

1. Вивчити означення понять, розглянутих на уроці.
2. Розв'язати вправи: на визначення виду подій, обчислення ймовірності випадкових подій за вивченою формулою (рі­вень складності завдань відповідає рівню складності завдань, розв'язаних на уроці).
3. Повторити схему розв'язування задач складанням математич­ної моделі.