Визначений інтеграл (план-конспект для ВНЗІ-ІІ р.а.)

Навчально – методична карта заняття

Предмет : математика

Тема заняття: визначений інтеграл

Тривалість заняття: 2 год

Тип заняття: комбінований

Група: І курс, «Лікувальна справа», «Сестринська справа»

І. Актуальність теми:

 Розробки лікарських препаратів, впровадження нових технологій фармацевтичного виробництва, кваліфіковане проведення біо фарма цевтич них, фармакологічних і клінічних досліджень, організація оптимального функціонування та економічної ефективності фармацевтичних закладів, прогнозування розвитку фармацевтичної науки вимагають від спеціаліста грунтовних знань з математики. Математична освіта сприяє формуванню абстрактного способу мислення, засвоєнню та розумінню біофізики.

ІІ. Навчальні цілі заняття:

 Студент повинен:

 Знати:

1.Означення визначеного інтегралу.

2.Властивості визначеного інтегралу.

3.Формулу Ньютона-Лейбниця.

    Вміти:

Використовуючи властивості визначеного інтегралу розв’язувати інтеграли, а також обчислювати площі геометричних фігур за допомогою визначеного інтегралу.

ІІІ. Цілі розвитку особистості (виховні):

• Сприяти формуванню абстрактного способу мислення
• Виховання в учнів культури математичної мови;
• Виховання бажання працювати в групі;
• Прививати інтерес до вивчення математики.

ІV. Міждисциплінарна  інтеграція:

 Забезпечуючі дисципліни:

Інформатика, фізика, біофізика.

V.Зміст теми заняття

Зміст теми заняття:

VІ.Зміст заняття

І. До поняття визначеного інтегралу приводить задача з визначення площі криволінійної трапеції.

Фігуру, обмежену неперервною кривою відрізком осі ОХ і прямими і називають криволінійною трапецією (мал.1). Розіб’ємо відрізок довільним чином на рівних частин. Точки поділу позначимо: З цих точок проведемо перпендикуляри до перетину з кривою

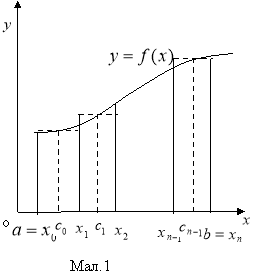   Отримаємо малих криволінійних                    трапецій, сума площ яких дає нам площу криволінійної трапеції. В центрі відрізків візьмемо точки і проведемо перпендикуляри (                                   штрихові лінії ) від цих точок до          перетину з кривою а потім побудуємо прямокутники, в основі яких лежать відрізки  , а висоти, відповідно, ординати Утворилася ступінчата фігура, площа якої наближається до площі криволінійної трапеції причому тим точніше, чим більше .

   Знайдемо

Всі доданки цієї суми відрізняються тільки індексами біля незалежної змінної, тому скорочено цю суму можна записати так:

                                                                                                   (1)

- це інтегральна сума. Символ (грецька буква “сигма”) означає, що потрібно додати вирази, що в правій частині (1), надаючи індексу всі цілі значення, починаючи від значення , вказаного під символом “сигма”, до значення, вказаного над цим символом.

   Якщо у виразі (1) збільшувати число так, щоб довжина відрізка = прямувала до нуля, то площа криволінійної трапеції буде дорівнювати границі інтегральної суми :

                                                                                                     (2)

   Границя інтегральної суми, при умові, що , називається визначеним інтегралом від функції на відрізку і позначається

                                                                                           (3)

де - нижня межа інтегрування, - верхня межа інтегрування, -змінна інтегрування.

   Не для всякої функції існує визначений інтеграл. Функція , для якої існує визначений інтеграл, називається інтегрованою на проміжку . Якщо

функція обмежена на проміжку і неперервна на ньому, то вона інтегрована на цьому проміжку.

   Якщо межі інтегрування є сталими величинами, то визначений інтеграл є стале число.

   Зв’язок між визначеним і невизначеним інтегралом встановлює формула Ньютона – Лейбніца:

                                                                                                 (4)             

де  і - значення первісної функції, взяті в точках  верхньої і нижньої границі.

                    ІІ. Властивості визначеного інтегралу.

   1. Визначений інтеграл не залежить від позначення змінної

                                  ,

оскільки результат інтегрування  - число, яке не залежить від того, якою буквою позначено аргумент підінтегральної функції.

   2. Визначений інтеграл від алгебраїчної суми скінченого числа неперервних функцій, заданих на відрізку дорівнює алгебраїчній сумі визначених інтегралів:

   .

   3. Сталий множник виноситься за знак визначеного інтегралу:

   4. Якщо верхню і нижню межі інтегрування поміняти місцями, то визначений інтеграл змінить знак на протилежний при збереженні абсолютної величини

   5. Якщо межі інтегрування рівні, то визначений інтеграл дорівнює нулю:

   6.       при  .

   7. Адитивна властивість: якщо проміжок розбити на дві частини і , то

   8. Якщо підінтегральна функція на проміжку інтегрування зберігає постійний знак, то інтеграл буде число того ж знаку, що і функція, тобто якщо , то            

   9. Якщо - найменше, а - найбільше значення функції на проміжку

то значення визначеного інтегралу знаходяться між добутками найбільшого і найменшого значення підінтегральної функції на довжину інтервалу інтегрування, тобто

        ІІІ. Методи обчислення визначених інтегралів.

   1. Обчислення визначених інтегралів за формулою Ньютона – Лейбніца.

   Визначений інтеграл обчислюється при допомозі невизначеного інтегралу згідно з формулою (4) і використанням властивостей визначеного інтегралу.

   Приклад.  Обчислити .

   2. Заміна змінної в визначених інтегралах.

   Для обчислення визначеного інтегралу   можна вводити нову змінну, якщо функція неперервна на , відрізок  є множиною значень функції визначеної на відрізку існує неперервна похідна функції на , а також виконується умова тоді

   Приклад. Обчислити інтеграл

Розв’язок. Введемо нову змінну , отримаємо

   Визначимо нові межі інтегрування: з рівності при отримуємо , а при - Тоді =

      3. Інтегрування визначеного інтеграла по частинах.

   Для визначеного інтеграла (аналогічно як для невизначеного) справедлива формула інтегрування по частинах:

ІV. Невласні інтеграли.

   Визначений інтеграл, розглянутий вище, введений для неперервної функції

на скінченому проміжку . Якщо проміжок інтегрування не скінчений, або підінтегральна функція розривна, то такі інтеграли називаються невласними.

   Якщо підінтегральна функція неперервна і скінчена при , то

                                                                             (5)

   Якщо границя в (5) скінченна, то невласний інтеграл називається збіжним, якщо інтеграл (5) не має скінченної границі, то він називається розбіжним.

   Геометрично невласний інтеграл являє собою площу криволінійної фігури, обмеженої даною лінією , віссю 0х і прямою х=а (мал.2 ).

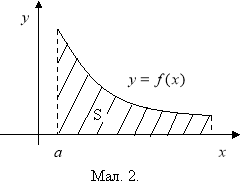
              Приклади.

   1. Знайти невласний інтеграл

   Розв’язок.

   Даний інтеграл розбіжний.

   2. Знайти інтеграл.

   Розв’язок. =

   Інтеграл збіжний.

                    V. Наближені обчислення визначеного інтеграла.

   Якщо підінтегральна функція задається графічним або табличним способом неможливо застосувати формулу Ньютона – Лейбніца для обчислення визначених інтегралів. В таких випадках використовують методи наближеного інтегрування.

   1. Формула прямокутників.

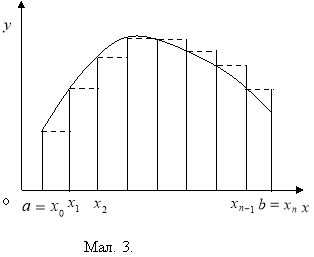   Проміжок інтегрування ділимо на частин точками (мал.3).

 Тоді формула прямокутника

.(6)

2. Формула трапецій.

   Якщо площі прямокутників (мал.3) замінити площами трапецій, то отримаємо формулу трапецій:

   .                          (7)

                  VI. Теорема про середнє значення.

   Якщо функція неперервна на проміжку , то існує така проміжна точка на , що визначений інтеграл від дорівнює добутку значення цієї функції в точці на довжину відрізка :

                                                                                                     (8)

   Значення функції називається середнім значенням функції на проміжку .

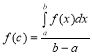       .                          (9)

Згідно з властивістю (9)

,

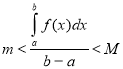 а, значить,

,

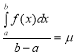де - число, що міститься між найменшим та найбільшим значеннями функції на проміжку . Оскільки на неперервна, то вона обов’язково набуде кожного значення між і . Тому, при деякому , що більше і менше , функція матиме значення

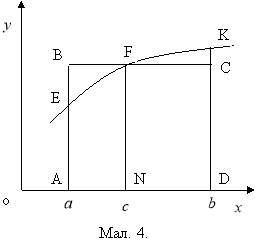
   Геометрично поняття середнього значення функції можна показати на мал.4.

   Інтеграл дає площу криволінійної трапеції АЕКD. Побудуємо прямокутник АВСD, площа якого дорівнює площі цієї трапеції. Тоді NF, звідки

                  NF=.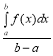

   Отже, середнє значення функції дорівнює значенню ординати NF.

   Поняття середнього значення функції використовується на практиці, оскільки багато величин характеризуються своїми середніми значеннями, наприклад середня швидкість хімічної реакції, середній тиск і інше.

VІІ. ЛІТЕРАТУРА

1.               Алгебра і початки аналізу. Підруч. для 10–11 кл. серед, шк. / А. М. Колмогоров, О. М. Абрамов, ІО. П. Дудніцин та ін.; За ред. А. М. Колмогорова. – К.: Освіта, 1992. - 350 с.
2.                Бевз Г. П. Методика розв'язування алгебраїчних задач. - К.: Рад. шк., 1975. - 240 с
3.               Бевз Г. II., Бевз В. Г., Владимирова II. Г. Геометрія: Проб, підруч. для 10 - 11 кл. загальноосвітніх навч. закл. - К.: Вежа, 2002. - 223 с.
4.               А.Н.Ремизов, Н.Х.Исакова, Л.Г.Максина «Сборник задач по медицинской и биологической физике»