Властивості функції: нулі функції, проміжки знакосталості, зростання і спадання функції.
Тема уроку. Властивості функції: нулі функції, проміжки знакосталості, зростання і спадання функції.
Мета уроку: сформувати знання учнів про зміст понять: нулі функції, проміжки, на яких функція зберігає свій знак (проміжки знакосталості функції), функція, що спадає на проміжку, та функція, що зростає на проміжку. Сформувати вміння відтворювати означення вивчених понять, а також розв'язувати задачі на знаходження нулів функції та на дослідження функцій на зростання та спадання на проміжку з використанням вивченого на уроці означення.
Тип уроку: формування знань та вмінь.
Наочність та обладнання: опорний конспект № 13.
Хід уроку
I. Організаційний етап
Учитель перевіряє готовність учнів до уроку, налаштовує їх на роботу.
II. Перевірка домашнього завдання
Для перевірки правильності виконання письмових вправ домашньої роботи можна організувати перевірку за зразком (якщо на попередньому уроці були труднощі з розв'язуванням вправ) або провести роботу у формі гри «Знайди помилку».
Засвоєння змісту теоретичного матеріалу перевіряється під час бесіди, або проведення математичного диктанту, або виконання тестових завдань [9, тест 8, завдання 1—3].
III. Формулювання мети і завдань уроку.
Мотивація навчальної діяльності учнів
Учитель нагадує учням зміст бесіди, проведеної на такому самому етапі попереднього уроку, акцентуючи увагу на тому, що, повторивши основні відомості про зміст поняття функції та супутніх з ним понять курсу 7 та 8 класів, на даному та наступному уроках учні мають опрацювати інші поняття, пов'язані з поняттям функції. Вивчення цих нових властивостей функції та вироблення вмінь їх застосовувати при розв'язуванні задач — це і є основна мета уроку.
IV. Актуалізація опорних знань та вмінь учнів
Усні вправи
- Розв'яжіть рівняння:
1) 2х + 1 = 0; 2) 1 – 2х = 0.
- Розв'яжіть нерівність:
1) 1 – 2х < 0; 2) 1 + 2х ≥ 0.
- При яких значеннях аргументу х f(x) = 0, якщо:
1) f(x) = l + 2x + x2; 2) f(x) = ![]() ?
?
- Функцію задано формулою f(x) = 3x – 1. Знайдіть:
1) f (1); 2) f (0); 3) f (x1); 4) f (x2).
V. Формування знань
План вивчення нового матеріалу
- Означення нуля функції. Проміжки знакосталості функції. Як знайти нулі та проміжки знакосталості функції, заданої графічно. Як знайти нуль функції, заданої формулою y = f(x).
- Означення функції, що зростає на проміжку.
- Означення функції, що спадає на проміжку.
- Як знайти проміжки зростання/спадання функції за її графіком,
- Як знайти проміжки зростання/спадання функції, заданої формулою y = f(x).
Методичний коментар
Властивості функції є матеріалом, який протягом достатньо тривалого часу традиційно вивчався у 9 класі після вивчення теми «Нерівності». Проте слід звернути увагу на те, що зміст навчального матеріалу з цієї теми у 9 класі 12-річної школи суттєво змінився: серед властивостей функції, що вивчаються у 9 класі, тепер немає понять парної та непарної функцій (це питання перенесено у 10 клас). Також вчителеві слід звернути увагу на те, що змінились програмові вимоги до знань та вмінь учнів. Так, серед вимог, що мають відношення до теми уроку, можна виділити таку: «учень характеризує функцію за її графіком». Однак автор вважає, що для формування повного уявлення про зміст понять «функція, що зростає/спадає на проміжку» слід ознайомити учнів зі способами дослідження функцій на зростання/спадання на даному проміжку не тільки за графіком, але й аналітично (за означенням).
У стислому вигляді зміст навчального матеріалу має вигляд опорного конспекту № 13.
Опорний конспект №13
|
Властивості функції |
||
|
1. Якщо для функції y = f(x) виконується умова f (х0) = 0 (х0 |
||
|
|
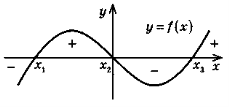
На рисунку х1, х2, х3 — нулі функції ( f (x1) = f (x2) = f (x3) = 0). Проміжки (-∞; x1), (x1; x2), (х2; х3), (х3; +∞) — проміжки знакосталості функції y = f(x). |
|
|
2. |
|
|
|
|
||
|
! Якщо необхідно визначити, чи є функція y = f(x) зростаючою/спадною на даному проміжку, то: |
||
|
а) покладають умову х2 > х1; |
||
|
б) записують різницю f(x2) – f(x1) та перетворюють її так, щоб можна було визначити її знак; |
||
|
в) якщо f(x2) – f(x1) > 0, то f(x2) > f(x1), і при умові х2 > х1 це означає, що f(x) зростає на даному проміжку; |
||
|
г) якщо f(x2) – f(x1) < 0, то f(x2)<f(x1), і при умові х2 > х1 це означає, що f(x) спадає на даному проміжку. |
||
VI. Формування вмінь. Відпрацювання навичок
Усні вправи
- Яке з чисел (значень змінної х) є нулем функції у = 3х2 – 2х – 1:
1) 1; 2) -1; 3) ![]() ; 4)
; 4) ![]() ?
?
- Відомо, що y = f(x) спадає на всій області визначення. Порівняйте:
1) f (3) і f (-3); 2) f (-2) і f (-3,5); 3) f ![]() і f
і f ![]() .
.
- Відомо, що y = g(x) зростає на всій області визначення. Порівняйте:
1) g(1) і g(0,1); 2) g![]() і g
і g![]() .
.
-
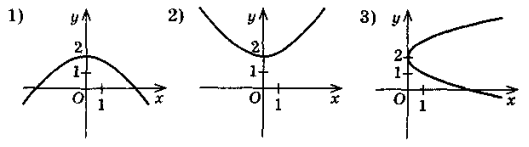
Відомо, що y = h(x) зростає, якщо х
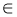 (-∞; 2], і спадає, якщо х
(-∞; 2], і спадає, якщо х 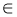 [2; +∞). Який із рисунків може бути зображенням графіка функції у = h(x)?
[2; +∞). Який із рисунків може бути зображенням графіка функції у = h(x)?
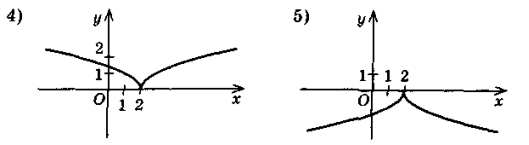
Письмові вправи
Вправи, запропоновані для розв'язування на цьому уроці, мають сприяти засвоєнню учнями змісту означень нуля функції, функції, що зростає на проміжку, та функції, що спадає на проміжку, і виробленню вмінь учнів виконувати дії для знаходження нулів функції, проміжків зростання та спадання функції за готовим графіком функції, а також із використанням формули у = f(x), що задає цю функцію.
Тому приблизний зміст вправ може бути таким:
- знайти нулі, проміжки знакосталості, проміжки зростання та проміжки спадання деякої функції, заданої графічно;
- за допомогою обчислень знайти нулі функції, заданої формулою y = f(x);
- за допомогою обчислень визначити, зростає чи спадає дана функція на заданому проміжку.
Методичний коментар
На даному уроці через систему усних і письмових вправ продовжується робота з відпрацювання навичок учнів виконувати тотожні перетворення раціональних виразів, розв'язувати раціональні та найпростіші ірраціональні рівняння, а також навичок роботи з графіками функцій (у декартових координатах).
VII. Підсумки уроку
Тестові завдання
- Числова функція задається:
а) рівнянням у = f(x); б) областю визначення;
в) аргументом; г) графіком.
- У рівнянні y = f(x) число х — це:
а) аргумент; б) область визначення;
в) функція; г) область значення функції.
- Множина всіх точок з координатами (x; f(x)), де y = f(x) — задана функція, це:
а) точка; б) лінія;
в) f(x); г) графік функції y = f(x).
- Функція y = f(x) спадна, якщо:
а) х2 < х1; б) f(x2) < f(x1);
в) при х2 > х1 f(х2) < f(x1); г) при х2 < х1 f(x2) < f(x1).
- Функція y = f(x) зростаюча, якщо:
а) при х2 > х1 f(x2) > f(x1); б) у2 > у1;
в) при х2 > х1 f(x2) < f(x1); г) х2 > х1.
VIII. Домашнє завдання
- Вивчити зміст понять, розглянутих на уроці (див. опорний конспект № 13).
- Розв'язати вправи, аналогічні за змістом та рівнем складності виконаним у класі.
- Повторити розв'язування лінійних нерівностей та їхніх систем і сукупностей.


про публікацію авторської розробки
Додати розробку