Властивості кутів, утворених при перетині двох паралельних прямих січною; властивості паралельних прямих
Тема. Властивості кутів, утворених при перетині двох паралельних прямих січною; властивості паралельних прямих
Мета: домогтися засвоєння учнями змісту теореми 5 (див. підручник) та схеми доведення від супротивного; виробити в учнів уміння відтворювати зміст вивчених тверджень та використовувати їх зміст при розв'язуванні задач на доведення; відпрацювати навички розв'язування задач на застосування ознак паралельності прямих.
Тип уроку: засвоєння знань, вироблення вмінь.
Обладнання: набір демонстраційного креслярського приладдя, таблиця № 7.
Хід уроку
І. Організаційний етап
ІІ. Перевірка домашнього завдання
Домашнє завдання (письмові вправи) перевіряємо за зразком під час самоперевірки, а засвоєння теорії — під час виконання математичного диктанту № 5.
Математичний диктант № 5
- Подивіться на дошку (рис. 43, а). Прямі АВ і CD паралельні. Чи обов'язково рівні кути 1 і 2 [2 і 3]?
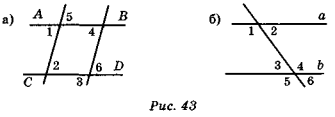
- Подивіться на дошку (рис. 43, а). Прямі АВ і CD паралельні. Чи обов'язково рівні кути 1 і 4 [3 і 4]?
- Подивіться на дошку (рис. 43, б). Прямі а і b паралельні. Які з позначених цифрами кутів дорівнюють куту 1 [3]?
- Подивіться на дошку (рис. 43, б). Прямі а і b паралельні. Які з позначених цифрами кутів дорівнюють куту 4 [2].
III. Мотивація навчальної діяльності учнів. Формулювання мети і завдань уроку
Для створення позитивної мотивації можна запропонувати учням розв'язати проблему:
За допомогою косинця і лінійки (див. алгоритм, вивчений у 6 класі) побудуйте прямі a, b і с так, щоб виконувалась умова а || с, b || с. Що можна сказати про прямі а і b, якщо а || с, b || с? Чи можуть прямі а і b мати спільну точку? Як перевірити правильність свого припущення?
Обговорення розв'язання проблеми приводить учнів до усвідомлення необхідності вивчення матеріалу уроку (це і є мотивація), а також дає змогу сформулювати узгоджену з учнями мету уроку.
IV. Актуалізація опорних знань і вмінь учнів
- Знайдіть усі невідомі кути, якщо а || b (рис. 44, а):
а) ![]() 1 = 20°; б)
1 = 20°; б) ![]() 1 =
1 = ![]() 2; в)
2; в) ![]() 1 = 3
1 = 3![]() 2.
2.
-
Дано: AS || CD, ВС || AD (рис. 44, б). Доведіть, що
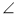 1 =
1 = 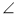 2;
2; 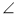 3 =
3 = 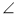 4.
4.
-
Укажіть взаємне розміщення прямих b і с, якщо а || b, с
 а.
а.
V. Засвоєння нових знань
План вивчення нового матеріалу
- Теорема про дві прямі, що паралельні до третьої.
- Метод доведення від супротивного.
Методичний коментар
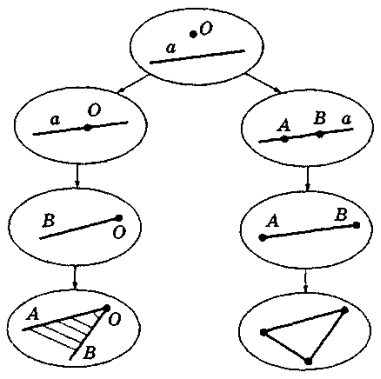
На відміну від традиційного підручника, новий підручник містить теорему про дві прямі, що паралельні до третьої, в розділі «Властивості паралельних прямих», хоча по суті є ознакою паралельності прямих (див. схему в таблиці № 8). Таке розташування навчального матеріалу можна пояснити єдиним способом доведення, який застосовано при доведенні теорем б, 7 способом від супротивного. Тому, щоб домогтися усвідомлення учнями цього факту перед формулюванням та доведенням теореми 5, можна запропонувати порівняти вивчені раніше доведення теореми 6, узагальнити отримані результати порівняння, а вже після цього сформулювати теорему 7 і застосувати при її доведенні попередньо узагальнену вищезазначену схему. Хоча новий підручник не містить цієї узагальненої таблиці № 8 (с. 61), автор вважає за доцільне сформулювати її у вигляді алгоритму з тим, щоб надалі усвідомлено використовувати її при розв'язуванні задач (схема № 5).
Схема № 5
VI. Первинне усвідомлення нового матеріалу. Закріплення знань та відпрацювання вивченого раніше матеріалу
Усні вправи
- Сформулюйте твердження, протилежне даному:
а) дві прямі паралельні;
б) два кути рівні;
в) сума двох кутів дорівнює 180°;
г) дві прямі перетинаються.
- Один із кутів, утворених при перетині двох паралельних прямих січною, дорівнює 120°. Чи може один з решти семи кутів мати міру 50° ? чому?
Письмові вправи
- На вироблення вміння міркувати за схемою методу від супротивного з підручника № 202, 203, 208.
- На відпрацювання вмінь застосовувати вивчені раніше властивості та ознаки паралельних прямих № 213, 216.
VII. Підсумки уроку
Усні вправи
За даними рисунка знайдіть кут х.
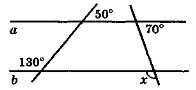
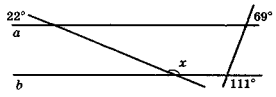
VIII. Домашнє завдання
- § 7 — вивчити теореми 6 і 7.
- Письмово: № 204, 214, 217.
- Повторити: основні геометричні фігури на площині та їх властивості (§ 1-5).


про публікацію авторської розробки
Додати розробку
