Розробка уроку на тему "Трикутник і його елементи"
Тема. Трикутник і його елементи
Мета: формування в учнів уявлення про зміст понять: медіана, бісектриса, висота трикутника, внутрішня та зовнішня області трикутника, кут трикутника; вироблення вмінь: на готовому рисунку розпізнавати медіани, висоти, бісектриси трикутника, називати його кути, виконувати зображення елементів трикутника; закріплення знань учнів про означення та властивості сторін трикутника і відпрацювання вмінь застосовувати ці знання при розв'язуванні задач.
Тип уроку: формування знань, вироблення вмінь.
Обладнання: набір демонстраційного креслярського приладдя, таблиця № 9 «Трикутник».
Хід уроку
І. Організаційний етап
ІІ. Перевірка домашнього завдання
Розв'язання домашніх задач учні перевіряють за готовими зразками (у вигляді або роздаткового матеріалу, або записів на дошці, або у вигляді проекції на екран).
Можна (за наявності часу) провести математичний диктант № 6 за вивченим на попередньому уроці матеріалом.
Математичний диктант № 6
- Виберіть три точки М, N, K [S, Р, Т] так, щоб:
а) вони не були вершинами трикутника;
б) були вершинами трикутника.
Назвіть цей трикутник.
- Назвіть:
а) вершини;
б) сторони трикутника FTK [MNO].
- Виконайте необхідні вимірювання і обчисліть периметр трикутника з п.1.
- Порівняйте довжину сторони МК із сумою довжин MN та NK [SP із сумою довжин ST та РТ]. Чи може бути, щоб MK > MN + NK [SP = ST + + PT]? Чому?
III. Формулювання мети і завдань уроку. Мотивація навчальної діяльності учнів
Запитання до учнів
- Назвіть геометричні фігури, з яких складається трикутник.
- Які властивості названих фігур ви знаєте?
- Як називаються елементи цих фігур, що ділять їх навпіл?
- Чи збережуться ці властивості в трикутнику?
Обговорення відповідей на ці запитання наводить на думку, що слід вивчити інші елементи трикутника, пов'язані з серединою сторони трикутника та бісектрисою його кута — це і є по суті основною дидактичною метою уроку.
IV. Актуалізація знань учнів
Усні вправи
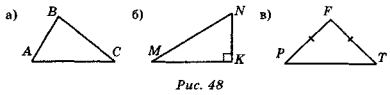
На рис 48:
а) назвіть елементи кожного з трикутників;
б) укажіть найбільший кут у кожному трикутнику, визначте його вид.
Як тепер можна назвати кожний з трикутників?
V. Засвоєння нових знань
План вивчення матеріалу
- Означення медіани трикутника; властивість медіан.
- Означення бісектриси трикутника; властивість бісектрис.
- Означення висоти трикутника; властивість висот.
- Положення висоти в трикутниках різних видів.
- Взаємне розміщення висоти, медіани, бісектриси, проведених з однієї вершини трикутника.
Методичний коментар
При вивченні нового матеріалу уроку традиційно вивчаються означення медіани, бісектриси та висоти трикутника і формулюються (без доведення) деякі властивості цих елементів (про перетин трьох медіан в одній точці і таке інше).
При цьому варто звернути увагу учнів на необхідність точного формулювання означень названих елементів трикутника (відпрацювати цей момент можна на усних вправах).
Хоча в підручнику на додаток до традиційного матеріалу розглядається питання про взаємне розміщення медіани, висоти і бісектриси, проведених з однієї вершини трикутника, автор вважає за необхідне додати до цього ще й матеріал про положення висоти, проведеної з вершини гострого кута трикутника.
VI. Первинне усвідомлення матеріалу
Усні вправи
-
У трикутнику DEF проведено відрізок ЕА (рис. 49). Визначте, чи є цей відрізок медіаною, бісектрисою або висотою даного трикутника, якщо: AF = DA;
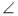 DAE =
DAE = 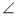 FAE;
FAE; 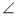 DEA =
DEA = 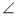 FEA.
FEA.
- Чи може всередині трикутника лежати тільки одна з трьох його висот; тільки дві з трьох його висот?
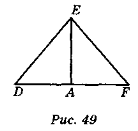
- Назвіть, чим є відрізки КС, NL, EF і DB в трикутниках КОР, MNK і ADE (рис. 50).
-
У трикутнику ABC проведено бісектрису ВК і медіану ВМ, АС = 8 см,
 ABC = 140°. Знайдіть довжину відрізка AM і градусну міру кута АВК.
ABC = 140°. Знайдіть довжину відрізка AM і градусну міру кута АВК.
Графічні вправи
- Накресліть три трикутники: гострокутний, тупокутний і прямокутний. Використовуючи косинець, проведіть у кожному з них висоту з вершини гострого кута
- Накресліть довільний трикутник. Скільки медіан можна в ньому провести? Побудуйте ці медіани, використовуючи лінійку з поділками.
Письмові вправи
- У трикутнику ABC сторони АВ і ВС рівні, BD — медіана. Периметр трикутника ABD дорівнює 21 см, а периметр трикутника CBD дорівнює 18 см. Знайдіть периметр трикутника ABC, якщо BD = 7 см.
- № 280.
VII. Підсумки уроку
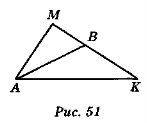
На рис. 51 зображено трикутник АМК. Зробіть необхідні позначки, щоб відрізок АВ був зображенням:
а) медіани; б) висоти; в) бісектриси трикутника.
VIII. Домашнє завдання
- § 9, с. 76 — вивчити означення.
- Письмово: № 262, 265, 279 на повторення № 288.


про публікацію авторської розробки
Додати розробку
