Презентація Геометрія 8 клас "Теорема Фалеса. Середня лінія трикутника та її властивості"

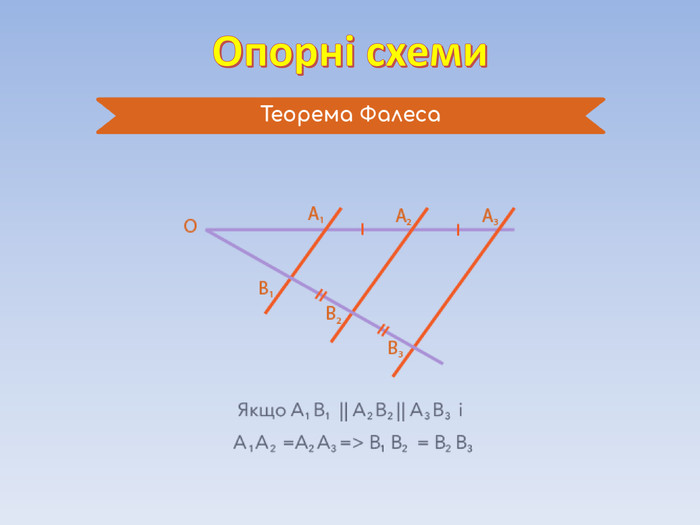
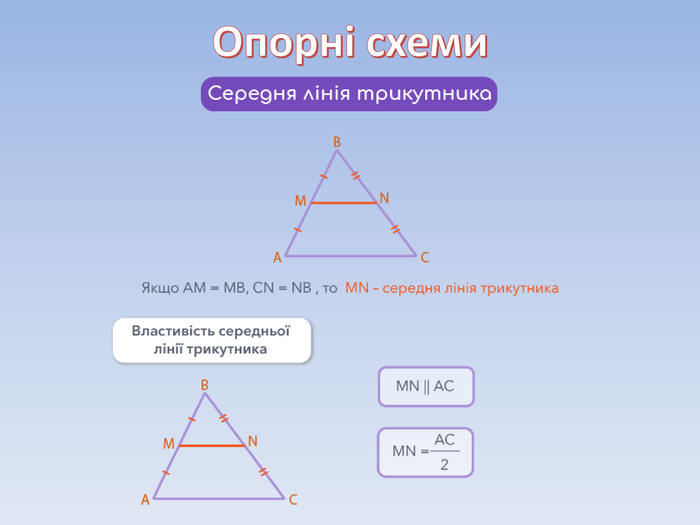
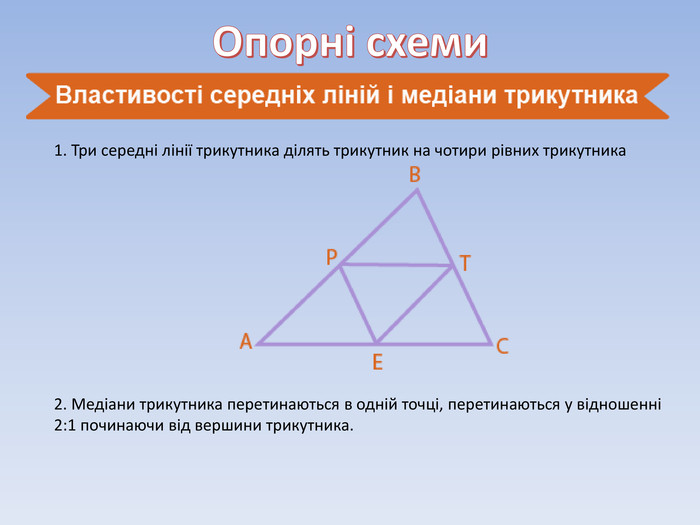
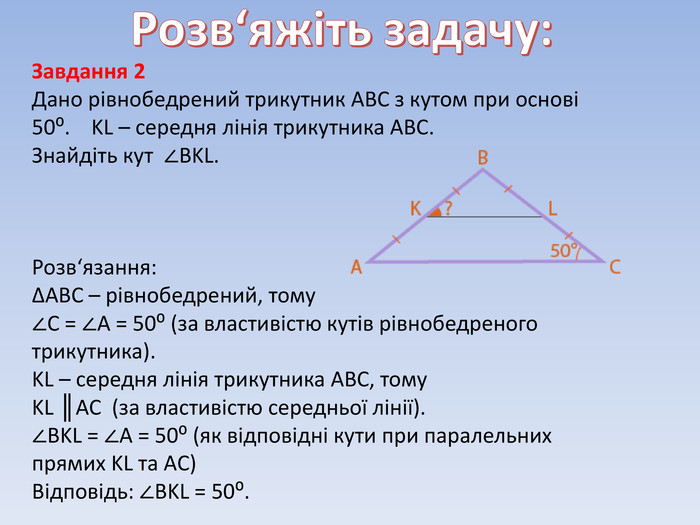
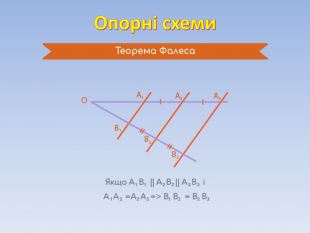
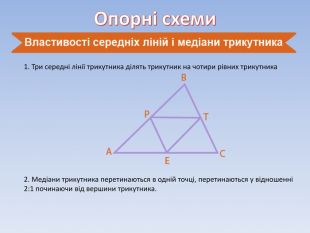
Тема уроку:8 В клас. ГЕОМЕТРІЯТеорема Фалеса. Середня лінія трикутника та її властивості.

ПРОСМОТР ПРЕЗЕНТАЦІЇ

Розглянемо відео Теорема Фалесаhttps://api.gioschool.com/api/v1/file/stream/7a3d71fb-0833-49e9-8eef-24f7a1d152dc

Опорні схеми

Опорні схеми

Опорні схеми1. Три середні лінії трикутника ділять трикутник на чотири рівних трикутника2. Медіани трикутника перетинаються в одній точці, перетинаються у відношенні 2:1 починаючи від вершини трикутника.

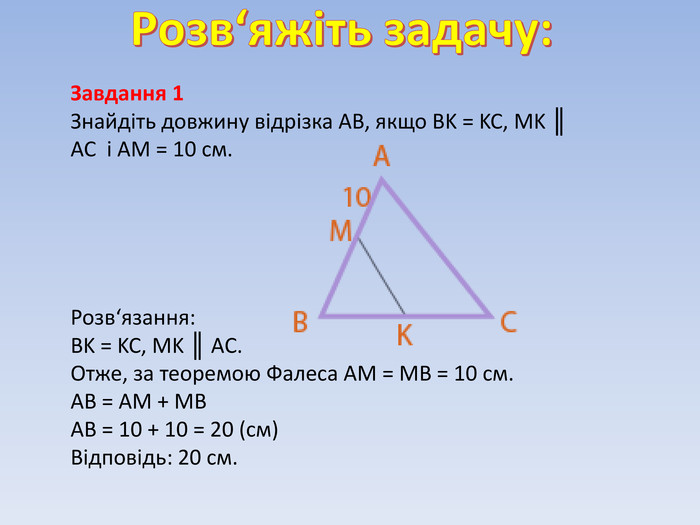
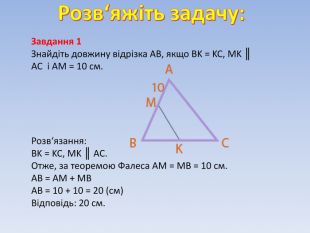
Розв‘яжіть задачу: Завдання 1 Знайдіть довжину відрізка АВ, якщо BK = KC, MK ║ AC  і АМ = 10 см. Розв‘язання: BK = KC, MK ║ AC.  Отже, за теоремою Фалеса АМ = МВ = 10 см. АВ = АМ + МВАВ = 10 + 10 = 20 (см)Відповідь: 20 см.

Розв‘яжіть задачу: Завдання 2 Дано рівнобедрений трикутник АВС з кутом при основі 50⁰.    KL – середня лінія трикутника АВС. Знайдіть кут  ∠BKL. Розв‘язання: ΔАВС – рівнобедрений, тому∠С = ∠А = 50⁰ (за властивістю кутів рівнобедреного трикутника). KL – середня лінія трикутника АВС, тому. KL ║AC  (за властивістю середньої лінії).∠BKL = ∠A = 50⁰ (як відповідні кути при паралельних прямих KL та AC) Відповідь: ∠BKL = 50⁰.

Розв‘яжіть задачу: Завдання 3 Сторони прямокутника дорівнюють 10 см і 18 см. Знайдіть відстань від точки перетину діагоналей прямокутника до його більшої сторони. Розв‘язання: ОК – відстань до ВС, тому ОК ⊥ ВС. АВ ⊥ ВС (бо АВСD прямокутник). Отже, АВ ║ОК. АО = ОС (за властивістю прямокутника)Отже, ВК = КС  (за теоремою Фалеса)Тому ОК – середня лінія трикутника АВС (за означенням). КО =        , КО =       = 5 (см)Відповідь: 5 см.

Розв‘яжіть задачу. Завдання 4 Сторони трикутника пропорційні числам 3, 7 і 8, а периметр трикутника, утвореного середніми лініями, дорівнює 36 см. Знайдіть найбільшу сторону трикутника. Розв‘язання: PT =    AC, PE =     BC, TE =     AB (за властивістю середньої лінії трикутника)Тож, PPTE =      PABC . PABC = 2 PPTE  = 2 ∙ 36 = 72 (cм)            ВС : АС : АВ = 3 : 7: 8 Нехай k – коефіцієнт пропорційності, тодіВС = 3 k, АС = 7 k, АВ = 8 k. АВ + ВС + АС = PABC 8 k + 3 k + 7 k = 7218 k = 72k = 4 АВ = 8 k = 8 ∙ 4 = 32 (см)– більша сторона Відповідь: 32 см.

Експрес - контрольhttps://learningapps.org/watch?v=p6gc52om320

Тренувальні вправи: По підручнику §9-10: №272, №290, №292, №297. Дякую за урок!