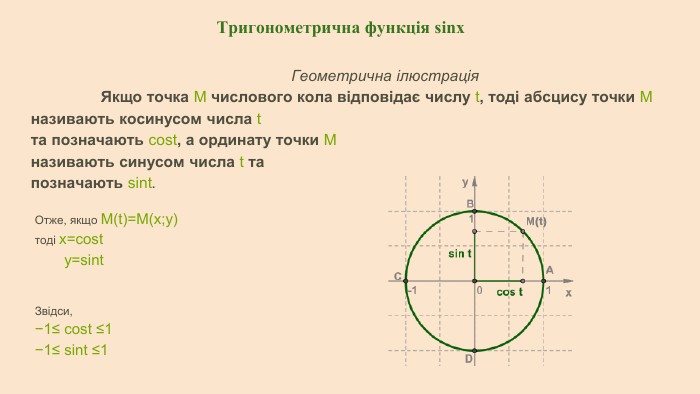
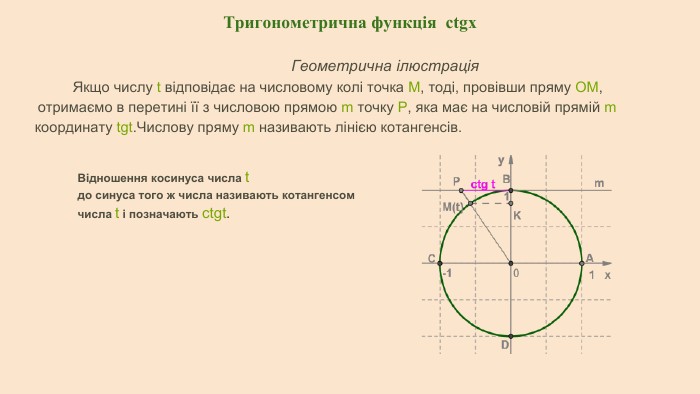
Властивості тригонометричних функцій sinx, ctgx
Про матеріал
Презентаційний матеріал до заняття на тему "Тригонометричні функції sinx, ctgx" Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку