Властивості тригонометричної функції

Тема: Властивості тригонометричної функції.

Мета: Вивчення властивостей тригонометричної функції у = sin х, у = cos х, у = tg х, у = ctg x (область визначення; множина значень; парність (непарність); симетрія графіка; періодичність; нулі; інтервали спадання (зростання); знакозмінні інтервали; максимальне і мінімальне значення).

Обладнання: інтерактивна дошка.

І. Перевірка домашнього завдання.

Вправа № 28. Перевірте правильність побудови графіків функцій (аг), використовуючи малюнок, намальований перед заняттям.

II. Вивчення властивостей тригонометричних функцій.

Властивості вивчених тригонометричних функцій зручно записати в Таблицю 2.1. При заповненні таблиці можливі такі коментарі:

1. Вирази sin х і cos х визначені для будь–яких x. Рівняння sin х і cos х визначені для будь–якого числа x, тому що для будь-якого числа x можна знайти координати точки , одиничного кола.

Вираз tg х має сенс для будь–якого x, крім чисел виду х = , n Ζ.

Вираз ctg x має сенс для будь–якого x, крім чисел виду х = πп, n Ζ.

2. Оскільки sin х і cos х — ордината й абсциса точки на одиничному колі, тому множиною значень синуса і косинуса є проміжок [–1; 1].

Оскільки tg α — вертикальна координата точки на дотичній лінії, то обла­сть дотичної лінії R.

Оскільки ctg α — є абсциса точки косинуса, то область косинуса дорівнює R (Рис. 2.17).

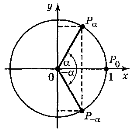
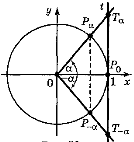
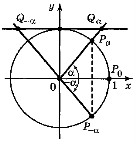
Рис. 2.17. Знаходження значень тригонометричних функцій

3. Оскільки точки Р_α і Р_–α розташовані осі ОХ, вони мають одну й ту саму абсцису та протилежні ординати, тобто sin (–α) = –sin α; cos (–α) = cos α.

Таблиця 2.1.

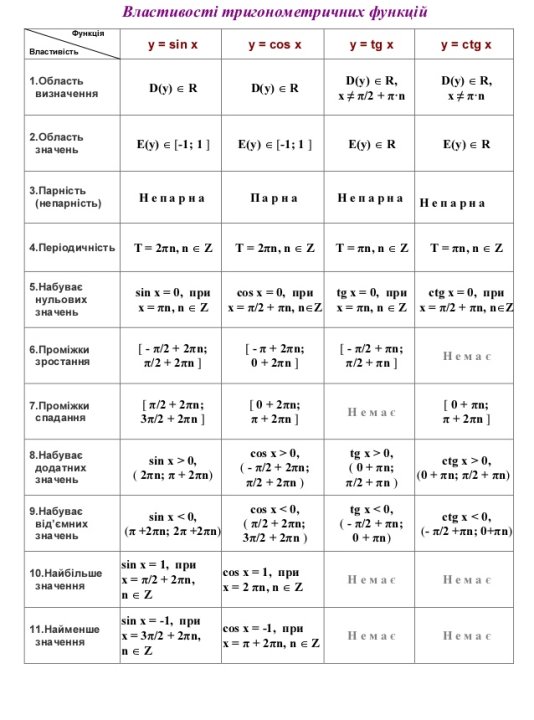
III. Застосування властивостей тригонометричних функцій до розв’язування вправ.

Виконання вправ

1. Використовувати властивості функції у = sin x, для порівняння чисел:

a) sin і sin ;  б) sin і sin ;  в) sin 3 і sin 4;   г) sin 1° і sin 1.

Відповідь: a) sin > sin ;  б)  sin > sin ;

   в) sin 3 > sin 4;           г) sin 1° < sin 1.

2. Розташувати числа в порядку зростання:

a) sin 20°; sin 85°; sin 30°; б) sin 0,2; sin 0,3; sin 0,1; в) sin 2; sin (–2); sin (–1); sin 1.

Відповідь: a) sin 20°; sin 30°; sin 85°;

  б) sin 0,1; sin 0,2; sin 0,3;  в) sin (–2); sin (–1); sin 1; sin 2.

3. Використовувати властивості функції у = cos x, для порівняня чисел:

1.      cos 2,52 і cos 2,53; б) cos (–4,1) і cos (–4); в) cos 1 і cos 3; г) cos 4 і cos 5.

Відповідь: a) cos 2,52 > cos 2,53;   6) cos (–4,1) > cos (–4);

   в) cos 1 > cos 3;          г) cos 4 < cos 5.

4. Розташувати числа в порядку зростання:

a) cos 13°; cos 53°; cos 23°;   б) cos 0,3; cos 0,6; cos 0,9; в) cos 2; cos 4; cos 6. Відповідь: a) cos 53°; cos 23°; cos 13°; б) cos 0,9; cos 0,6; cos 0,3;

в) cos 4; cos 2; cos 6.

5. Використовувати властивості функції у = tg x, для порівняня чисел:

а) tg (–2,6π) і tg (–2,61π);  б) tg 2,7π і tg 2,75π; в) tg 2 і tg 3; г) tg 1 і tg 1,5.

Відповідь: а) tg (–2,6π) > tg (–2,61π);   б) tg 2,7π < .tg 2,75π;

   в) tg 2 < tg 3;    г) tg 1 < tg 1,5.

6. Розташувати числа в порядку зростання:

a) tg 25°; tg 65°; tg 15°;     б) tg (–1); tg (–2); tg (–3);     в) tg (–5); tg (–3); tg 3.

Відповідь: а) tg 15°; tg 25°; tg 65°;   б) tg (–1); tg (–3); tg (–2);

  в) tg 3; tg (–3); tg (–5).

IV. Підсумок уроку.

V. Домашнє завдання.

Розділ І § 7. Запитання і завдання для повторення до розділу І № 52-56, Вправи № 18 (а-г), № 35 (1-4). Повторити розділ І §1-6.