Внеклассное мероприятие + презентация "Магические квадраты"

 

 

 

 

 

 

 

 

.

 

 

 

 

 

ВНЕКЛАССНОЕ МЕРОПРИЯТИЕ ПО МАТЕМАТИКЕ

«Магические квадраты»

 

 

 «…математические истины бессмертны, не подвержены тлению и остаются одинаковыми вчера, сегодня и вечно».                       

    Эрик Темпл Белл

 

 

 

 

 

 

 

 

 

 

 

 

Выполнила Марко Наталья Юрьевна

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Внеклассное мероприятие по математике

Устный журнал «Магические квадраты».

 

Форма проведения: устный журнал.

 

Цель: привлечь внимание обучающихся к предмету математики.

 

Задачи::

 -  формировать умение использовать знания в нестандартной ситуации;

 -  развивать самостоятельность и ответственность за  результаты своей деятельности;

 - формировать доброжелательное отношение к одноклассникам, учить   толерантности;

 - воспитывать коммуникативные навыки общения; умения слушать и слышать;

 - стимулировать интерес к математике через элементы историзма.

 

Компетенции:

ОК 2. Организовывать собственную деятельность, исходя из цели способов ее  

            достижения. (компетенция личностного самосовершенствования)

ОК 6. Работать в коллективе и команде. (коммуникативная  компетенция)

 

Оборудование и оформление:

- проектор, экран,

- листы бумаги, ручки,

- презентация  устного журнала «Магические квадраты»;

 

План мероприятия.

1. Объявление темы, цели мероприятия.

2. Выступление ведущих по страницам устного журнала:

    1 страница «Историческая» - история возникновения магических квадратов.

    2 страница «Познавательная» - виды и свойства магических квадратов.

    3 страница «Практическая» - простые способы составления магических квадратов.

    4 страница «Исследовательская» - области применения магических квадратов.
    5 страница «Занимательная» - определение своего характера с помощью квадрата                   

                                                         Пифагора.

    6 страница «Заключительная» - выводы.

3. Итоги мероприятия.

 

 

 

 

 

 

 

 

Ход мероприятия.

Устный журнал «Магические квадраты»

Ведущий: Добрый день!  

СЛАЙД 1   

     Священные, волшебные, загадочные, таинственные, совершенные… Как только их не называли. - ”Я не знаю ничего более прекрасного в арифметике, чем эти числа, называемые некоторыми планетными, а другими - магическими»” - писал о них известный французский математик, один из создателей теории чисел Пьер де Ферма. Привлекающие естественной красотой, наполненные внутренней гармонией, доступные, но по-прежнему непостижимые, скрывающие за кажущейся простотой множество тайн... Знакомьтесь: 

  СЛАЙД 2   магические квадраты - удивительные представи­тели воображаемого мира чисел.   На страницах нашего журнала мы познакомим вас с историей возникновения и развития магических квадратов; с их свойствами; с основными методами построения магических квадратов и рассмотрим области их применения, а также проверим утверждение  Пифагора о том, что судьба человека зависит от числа его рождения. 

 СЛАЙД 3  1 страница «Историческая»      

СЛАЙД 4

ИМПЕРАТОР Выходит ученик в костюме императора:

«Далёкое время

Застыло на камне,

А мы прикоснулись к нему.

Попала к нам в руки

Великая тайна,

Мы сбросим веков пелену».

Здравствуйте, дети! Я – китайский мудрец и император Ю, живший более 4 тысяч лет назад. Однажды я гулял по берегу реки Хуанхэ. И вдруг увидел черепаху. На её панцире был начертан таинственный узор, напоминающий форму квадрата.

« Да, она священна!», - воскликнул я.

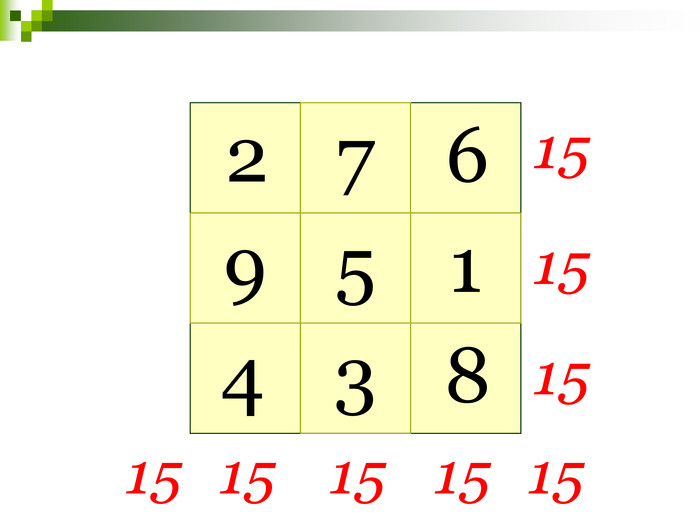
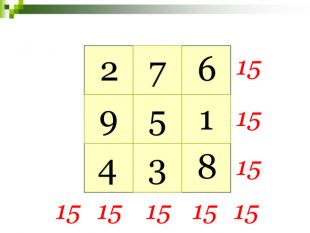
 Линии узора складывались таким образом, что можно было разглядеть числа от 1 до 9, причем эти числа были расположены таким образом, что во всех направлениях, будь то вертикаль, горизонталь или диагональ, их сумма была равна 15.

Эти знаки сейчас известны под названием Ло-Шу и равносильны магическому квадрату.

 

СЛАЙД 5

ИСТОРИК Математические или волшебные квадраты были известны еще арабам и индусам. В Европе они появились в 15 веке благодаря византийскому писателю Мосхопуло.

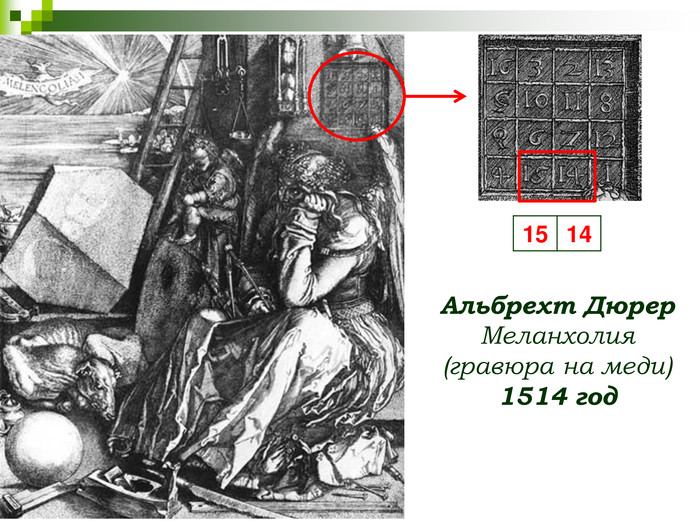
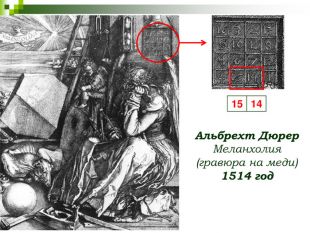
СЛАЙД 6 Первым квадратом, придуманным европейцем, считается квадрат Альбрехта Дюрера, изображенный на его знаменитой гравюре «Меланхолия». Дата создания гравюры - 1514 год - указана числами, стоящими в двух центральных клетках нижней строки. Говорят, что гравюра Дюрера послужила толчком для знаменитых пророчеств его современника Мишеля Нострадамуса.

СЛАЙД 7  Магические квадраты очень уважали и приписывали им различные мистические свойства. Говорят, если надо было решиться на какое-то опасное дело, их с магическими целями рисовали на бумажке и съедали. Такое же кушанье предлагали в качестве панацеи от всех болезней. Бытовало поверье, что выгравированный на серебре магический квадрат защищает от чумы. Даже сегодня среди атрибутов европейских прорицателей можно увидеть магические квадраты.

СЛАЙД 8

2 страница «Познавательная»      

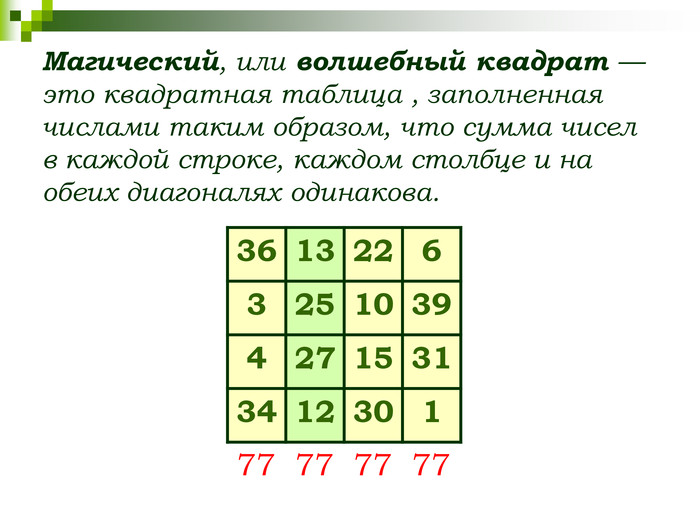
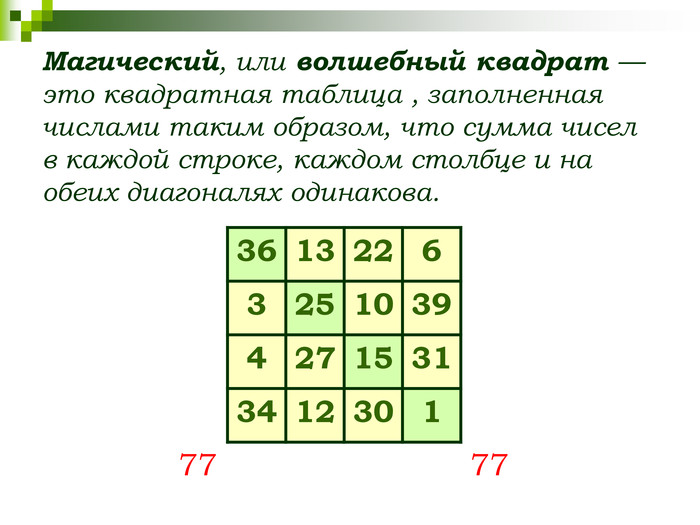
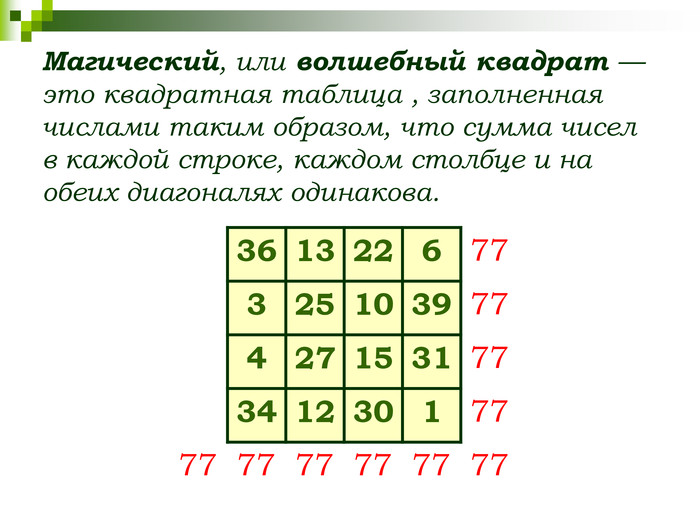
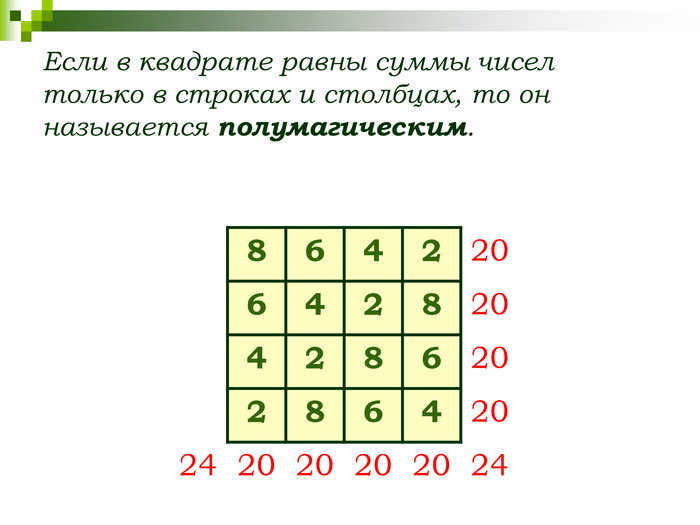
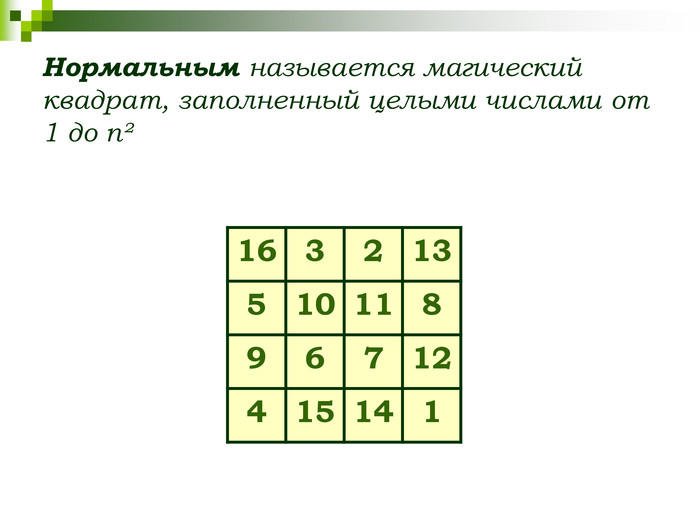
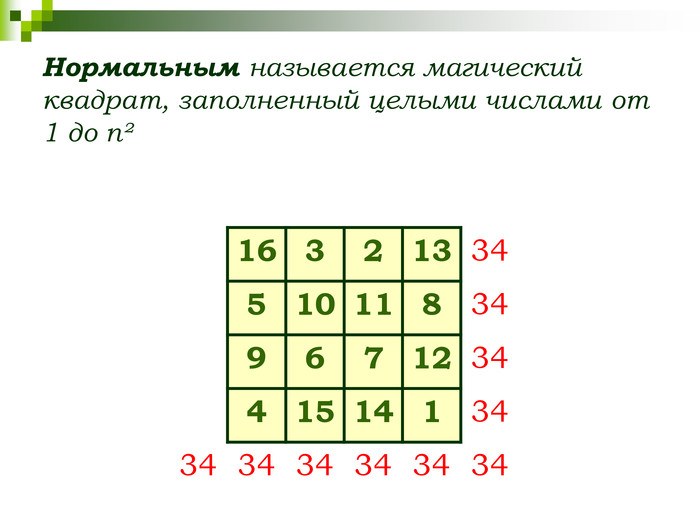
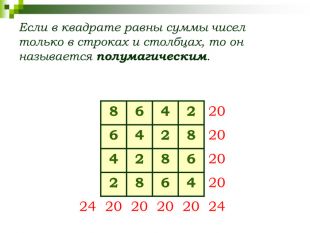
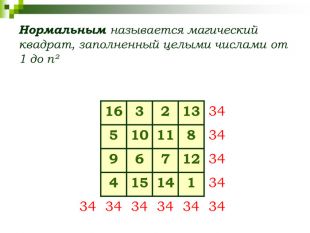
СЛАЙД 9  Магический, или волшебный квадрат — это квадратная таблица, заполненная n² числами таким образом, что сумма чисел в каждой строке, каждом столбце и на обеих диагоналях одинакова. Если в квадрате равны суммы чисел только в строках и столбцах, то он называется полумагическим. Нормальным называется магический квадрат, заполненный целыми числами от 1 до n².

СЛАЙД 10 Поля таблицы, в которые записывают числа, называются клетками магического квадрата, а сумма чисел, стоя­щих в любой строке, столбце или на диагонали, - его постоянной или магической константой.

СЛАЙД 11  Полного описания всех возможных магических квадратов не получено и до сего времени

    Известно, что магических квадратов 2х2 не существует. Магических квадратов 3х3 – один – остальные такие квадраты получаются из него поворотами и симметриями. Расположить натуральные числа от 1 до 9 в магический квадрат 3х3 можно 8 различными способами. Магических квадратов 4х4  уже более 800, а количество магических квадратов 5х5 близко к четверти миллиона.

Магические квадраты обладают следующими свойствами:

СЛАЙД 12

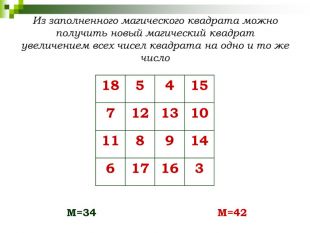
1.               Если все числа в клетках магического квадрата увеличить на одно и то же число, то получим магический квадрат.   

СЛАЙД 13

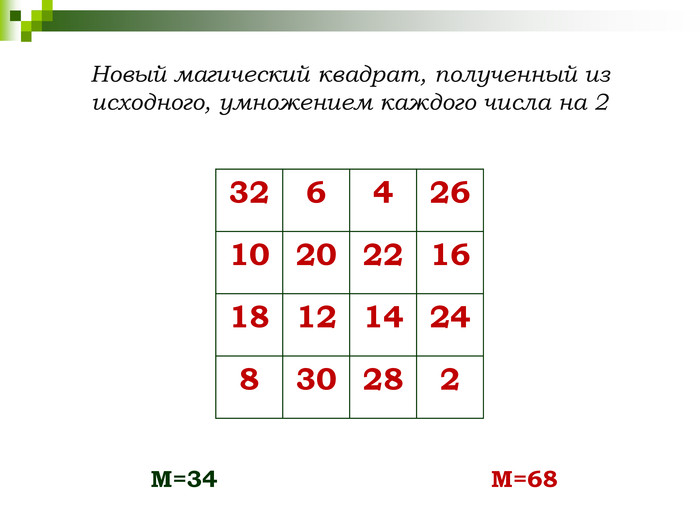
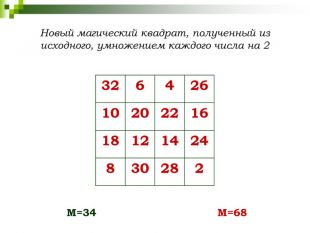
2.               Если все числа в клетках магического квадрата умножить на одно и то же число, то также получим магический квадрат.

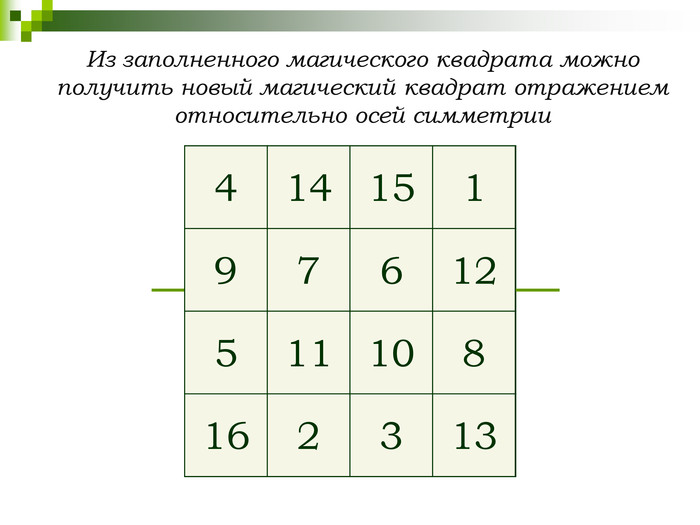
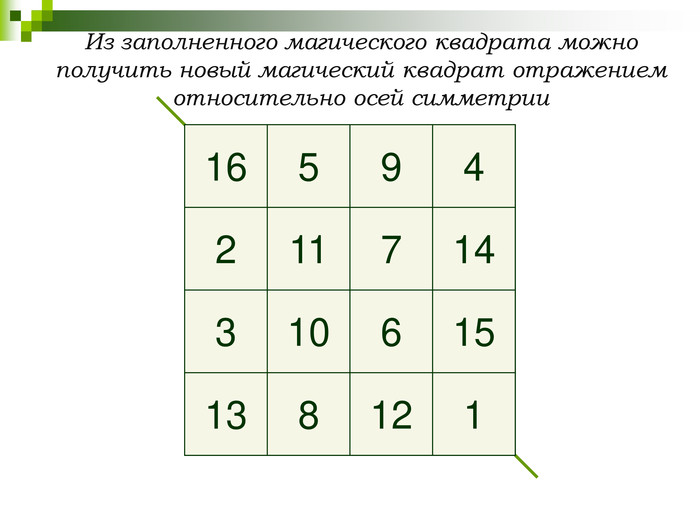
СЛАЙД 14, СЛАЙД 15, СЛАЙД 16, СЛАЙД 17

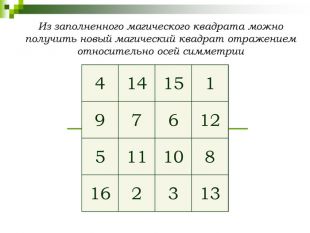
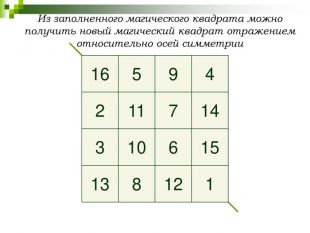
3.   При отражении, относительно одной из осей симметрии магического квадрата получим тоже магический квадрат.   

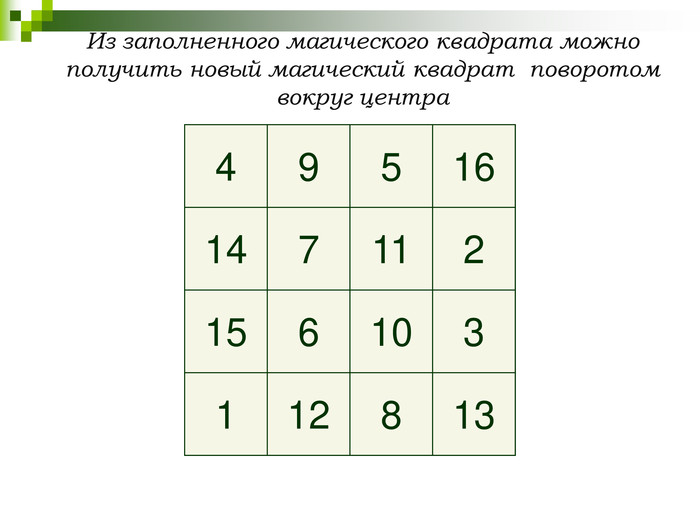
СЛАЙД 18

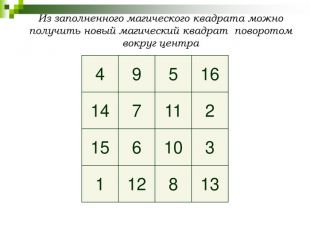
4. При повороте вокруг центра на угол магического квадрата, получим магический квадрат.   

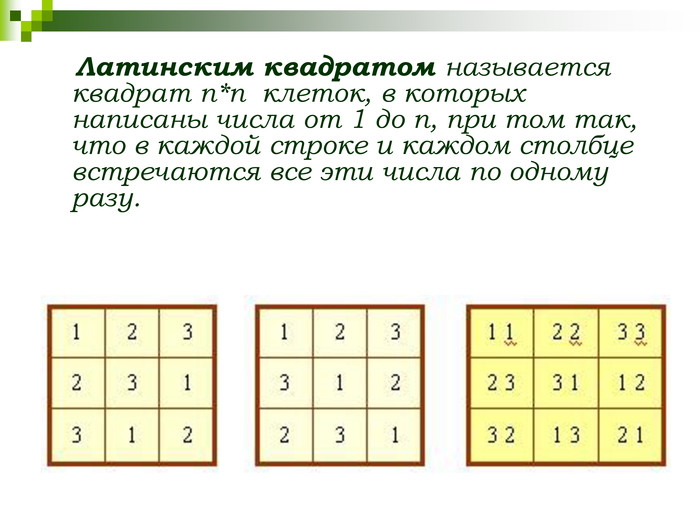
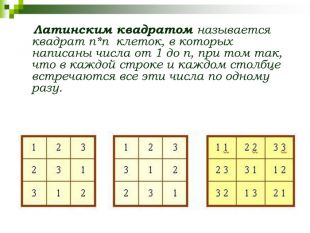
          СЛАЙД 19    Латинским квадратом называется квадрат n*n  клеток, в которых написаны числа от 1, до n, при том так, что в каждой строке и каждом столбце встречаются все эти числа по одному разу. Они обладают интересной особенностью: если один квадрат наложить на другой, то все пары получившихся чисел оказываются различными. Такие пары латинских квадратов называются ортогональными.

СЛАЙД 20    3 страница «Практическая»

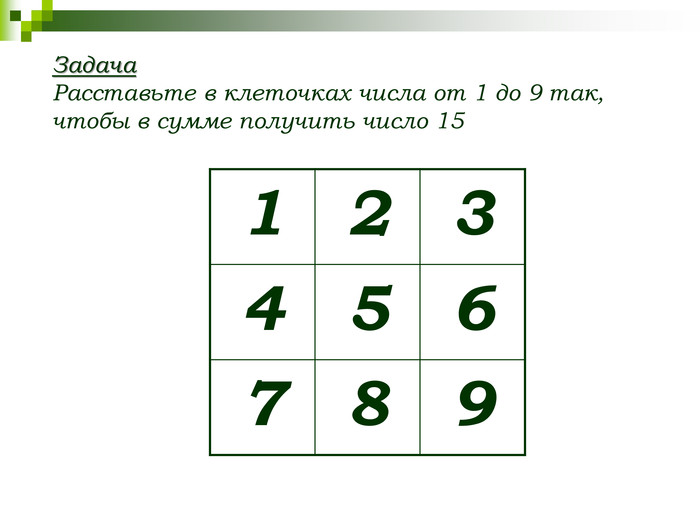
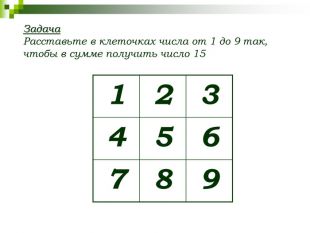
Хочу предложить вам задачу: заполнить квадрат 3*3 натуральными числами от 1 до 9 так, чтобы были использованы все цифры и сумма чисел на всех строках, столбцах и диагоналях была одинакова. Даю подсказку – сумма равняется 15.

С давних пор математики стремились решить две основные задачи, связанные с магическими квадратами: найти общий метод их построения и описать все возможные магические квадраты. И хотя для каждого вида квадрата были найдены свои способы решения задачи, пока не известен общий, пригодный для квадратов любого порядка, метод их построения. Мы рассмотрим самый простой и доступный практически всем способ.

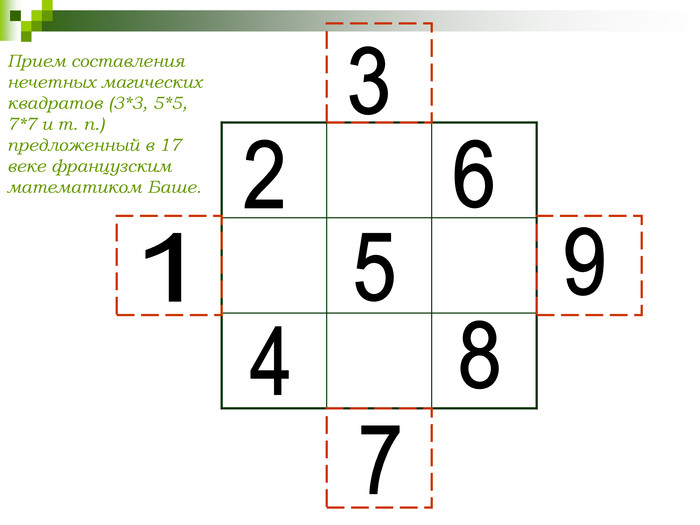
         СЛАЙД 21    Старинный прием составления нечетных магических квадратов, то есть квадратов из любого нечетного числа клеток: 3х3, 5х5, 7х7 и т.п. Прием этот предложен в XVII веке французским математиком Баше. Способ Баше пригоден и для 9- клеточного квадрата. Мы начнем исследование способа именно с этого примера. Итак, приступим к составлению 9- клеточного магического квадрата по способу Баше.

    Начертим квадрат, разграфленный на девять клеток. Приведем наш квадрат к виду ромба, достроив по 1 клеточке с каждой стороны. Впишем по порядку числа от 1 до 9, располагая их косыми рядами по три в ряд.  

        Числа, стоящие вне квадрата, вписываем внутрь его так, чтобы они примкнули к противолежащим сторонам квадрата (оставаясь в тех же столбцах или строках, что и раньше). В результате получаем квадрат.

            Применим правило Баше к составлению квадрата из 5х5 клеток.

СЛАЙД 22

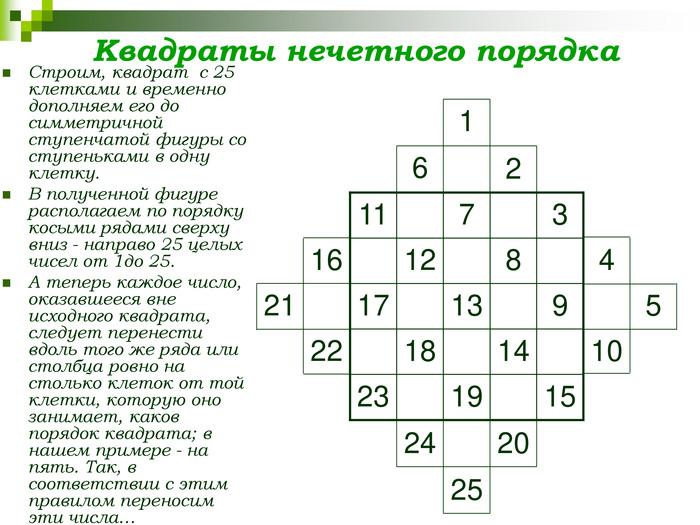
     - Строим, квадрат с 25 клетками и временно дополняем его до, симметричной ступенчатой фигуры (того же ромба) со ступеньками в одну клетку.

     -    В полученной фигуре располагаем по порядку косыми рядами сверху вниз - направо 25 целых чисел от 1до 25.

    -     А теперь каждое число, оказавшееся вне исходного квадрата, следует перенести вдоль того же ряда или столбца ровно на столько клеток от той клетки, которую оно занимает, каков порядок квадрата, в нашем примере - на пять. Так, в соответствии с этим правилом переносим эти числа…

Квадраты, составленные по указанной схеме, будут всегда магическими симметрическими

СЛАЙД 24    4 страница «Исследовательская»

         Когда мы рассмотрели способы составления магических квадратов, нас заинтересовала область их применения. Она показалась нам довольно таки интересной.

СЛАЙД 25      Традиционной сферой применения магических квадратов являются талисманы. К примеру, талисман Луны обладает определенными свойствами: предохраняет от кораблекрушения и болезней, делает человека любезным, способствует предотвращению дурного намерения, а так же укрепляет здоровье.

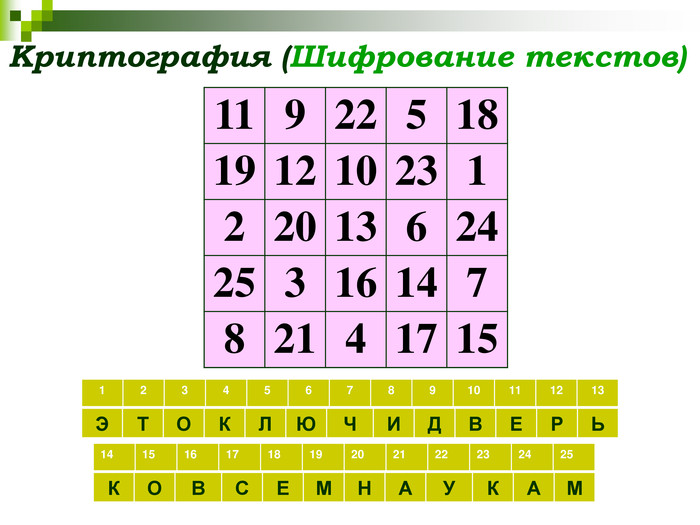
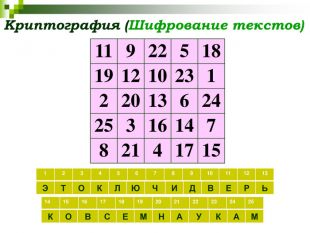
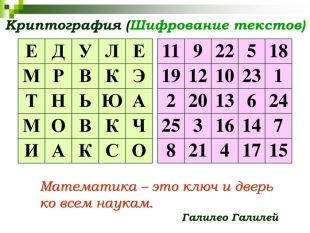
СЛАЙД 26 Сегодня очень актуальным становится вопрос о защите информации. Магические квадраты применяются в криптографии для шифровки и расшифровки сообщений. Как вы думаете, легко ли расшифровать эту фразу?

Е	Д	У	Л	Е
М	Р	В	К	Э
Т	Н	Ь	Ю	А
М	О	В	К	Ч
И	А	К	С	О

– Действительно, расшифровать её практически невозможно если у вас нет магического квадрата при помощи которого она и была зашифрована.

Сейчас попробуем это сделать вместе. Этот магический квадрат 5 порядка – и есть наш ключ!

11	9	22	5	18
19	12	10	23	1
2	20	13	6	24
25	3	16	14	7
8	21	4	17	15

Математика – «это ключ и дверь ко всем наукам» (Галилео Галилей).

Теперь вы и сами сможете зашифровать что-нибудь с помощью магических квадратов, если учесть, что квадратов 5 порядка существует, как мы знаем, более 275 млн. прочесть ваше сообщение вряд ли кто-нибудь сможет. Для этого понадобиться супер компьютер. Расшифровать сообщение сможет только тот, кому вы сообщите квадрат-ключ.

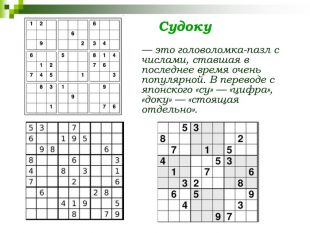
СЛАЙД 27 Так же очень популярна головоломка «судоку», прародителем которой можно считать Магический квадрат. Многие считают, что «судоку» является японским развлечением, но на самом деле Япония может считаться только родиной названия.

        По некоторым данным решения головоломок «судоку» улучшает память, логику мышления, а также препятствует развитию и даже лечит заболевания связанные с головным мозгом (такие, как болезнь Альцгеймера). Потому, ученые рекомендуют ежедневно решать кроссворды «судоку».

   СЛАЙД 28  Использование ортогональных латинских квадратов помогает учесть все возможные варианты в экспериментах в сельском хозяйстве, физике, химии, технике.

СЛАЙД 29 В последние годы магические квадраты - элементы прогресса нанотехнологий. Фирма «Toshiba»,  разрабатывая качественные телевизионные экраны, пришла к выводу, что цветовые ячейки выгодно компоновать по принципу магических квадратов. В этом случае резко повышаются как четкость изображений, так и цветовые переходы.

СЛАЙД 30   5 страница «Занимательная»

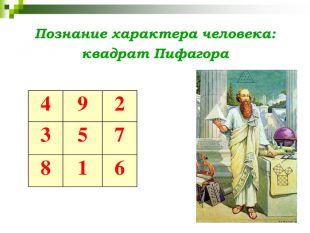
СЛАЙД 31    Изучая магические квадраты, мы обнаружили еще один занимательный квадрат - квадрат Пифагора, представляющий исторический интерес и полезный для составления психологического портрета личности.

СЛАЙД 32 Выполняя несложные расчеты с цифрами даты своего рождения, мы получили вот такие квадраты.

Предлагаем сейчас вам сделать свои квадраты. На моем примере

Я родилась 25 мая 2007 года. Записываем: число, месяц, год без нулей (порядок не нарушать): 25527.

1. Вычислим первое число: для расчета первого числа необходимо сложить все цифры числового ряда даты рождения 2+5+5+2+7= 21, первое число – 21

2. Вычислим второе число: для расчета второго числа необходимо сложить цифры, из которых состоит первое число 2+1=3, второе число – 3.

3. Вычислим третье число: для расчета третьего числа необходимо вычесть из первого числа первую цифру всего ряда (в моем примере цифра 2), умноженную на постоянный множитель – 2.

21 – 2 ∙ 2 = 17, третье число – 17.

4. Вычислим четвертое число. Для вычисления четвертого числа необходимо сложить цифры, из которых состоит третье число 1+7=8, четвертое число – 8. Запишем полученные числа под датой рождения:

	25527
	213178
11		-	77
222		55	8
3		-	-

Выпишем одинаковые цифры в математический квадрат Пифагора (кроме цифры 0).

По каждому качеству определите процент совпадения с вашими представлениями о себе.

Ячейки квадрата означают следующее:

Ячейка единиц – целеустремленность, воля, упорство, эгоизм.

Количество двоек определяет уровень эмоциональности, душевности, чувственности, биоэнергетики.

Ячейка троек – точность, аккуратность, пунктуальность.

Ячейка четверок – здоровье.

Ячейка пятерок – интуиция

Ячейка шестерок –материальность, расчет.

Количество семерок определяет меру таланта.

Количество восьмерок определяет степень чувства долга.

Ячейка девяток – ум, мудрость.

Если вас заинтересовала более подробная расшифровка, то с ней сможете ознакомится на интернет страницах.

СЛАЙД 34  

 Но не следует слепо верить всему магическому. Может быть, некоторые черты характера и заложены в дате рождения человека, но человек всегда может найти способы что-то изменить в своей судьбе, попытаться помочь себе и  близким стать лучше.

СЛАЙД 35   6 страница «Заключительная»

СЛАЙД 36  В завершении нашего журнала хотелось бы отметить: несмотря на то, что собственно магические квадраты пока не нашли широкого применения в науке, технике и жизни человека, они подвигли на занятия математикой множество незаурядных людей и способствовали развитию некоторых разделов математики: теории групп, матриц, комбинаторного анализа, а также способствуют улучшению памяти, развитию умения просчитывать ход своих мыслей на несколько шагов вперед.

СЛАЙД 37  У современной молодежи приоритетными являются  престижные и «комфортные» профессии, и мы считаем, что использование квадрата Пифагора для определения своих возможностей и способностей, заложенных природой, поможет с выбором профессионального пути.

СЛАЙД 39  Спасибо за внимание!

Ведущий: В условиях отсутствия компьютеров и ограниченного пространства доступных числовых конструкций, магические квадраты десятки веков приводили людей в неописуемый, доходящий до экзальтации восторг, когда они как чуду внимали совершенству незатейливых суммирующих закономерностей.

Сегодня этим уже никого не удивишь. Человек научился строить магические квадраты самой разной природы и порядка. И то, что раньше казалось таинством, сегодня представляется ремеслом.