Вплив викладання математики за програмою «Росток» на роботу у класах з поглибленим вивченням предмету.

Вплив викладання математики за програмою «Росток» на роботу у класах з поглибленим вивченням предмету.

                                               Жакоміна Тетяна Михайлівна

                                вчитель математики

                                             Бериславського ЗПЗСО №3

В сучасній освіті інтенсивно розвиваються процеси активізації науково - педагогічної ініціативи та творчості на засадах діяльнісного підходу. Результатами такої ініціативи стають нові моделі та концепції освіти, технології навчання і виховання, нові програми, підручники та посібники, створюються навчальні заклади нового типу.

Перед нами, вчителями, стоїть актуальна проблема – практичне втілення результатів педагогічної творчості у зміст і методи навчання та виховання підростаючого покоління.

Школа, у якій я працюю, обрала для себе такий шлях розв’язання цієї проблеми як викладання предметів природничо –математичного циклу за програмою науково-педагогічного проекту «Росток» у молодшій та середній ланці, а починаючи з 8-го класу у класах з поглибленим вивченням математики. Тому я поставила перед собою завдання дослідити як впливає навчання учнів за програмою «Росток» на їх подальшу роботу в класах з поглибленим вивченням математики.

В курсі математики, що вивчається у 5-6-х класах та алгебри, геометрії у 7-му класі за програмою «Росток» можна виділити такі лінії:

• арифметична;
• алгебраїчна;
• теорії чисел;
• ймовірнісна;
• мови і логіки;
• геометрична.

Кожна з цих ліній разом із задачами розвиваючого навчання сприяють інтелектуальному розвитку учнів, розвитку їх здібностей та рефлексивному аналізу їх власної діяльності. Це дає змогу учням перейшовши до класу з поглибленим вивченням математики працювати більш самостійно і впевнено.

Зупинимося окремо на кожній з цих ліній.

Основою вивчення математики є арифметика. Чітке виконання дій, обчислення без помилок є запорукою успішного навчання у старших класах. Програма «Росток» включає багато цікавих вправ обчислювального характеру. Це дає змогу навчити учнів швидко рахувати,  як усно так і письмово.

Алгебраїчна лінія цієї програми починається з 5-го класу і містить такі розділи:

• розв’язування рівнянь;
• розв’язування задач за допомогою рівнянь;
• перетворення алгебраїчних виразів.

Зупинимося коротко на кожному з цих розділів. Приходячи до 5-го класу учні вже вміють розв’язувати рівняння з двома, трьома і більше діями, а на протязі 5-6-го класів вдосконалюють свої знання та повністю закінчують вивчення лінійних рівнянь. Це сприяє розвитку логічного мислення та удосконаленню обчислювальних навичок учнів. Наведемо приклади рівнянь, що пропонуються за програмою «Росток»

4,44-(у:4,04-40,4):4=0,04;

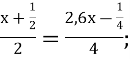
-6(у+2,5)-4у=7(1-2у);

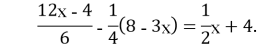
Розв’язування великої кількості рівнянь дозволяє швидше перейти до задач на складання рівнянь. Вивчення математики у 5-му класі за програмою «Росток» починається з теми «Переклад умови задачі на математичну мову». Під час її вивчення учні навчаються математичному моделюванню. Вони розв’язують стандартні задачі на рівняння, задачі рівняння до яких розв’язуються методом спроб і помилок та методом перебору, та задачі до яких рівняння тільки складаються.  У 6-му класі закріплення цієї тему відбувається при вивченні  тем «Відсотки» і «Пропорції», де новий матеріал поєднується з раніше вивченим .

Наведу приклад задачі із підручника «Математика 5. Частина 1» автори Дорофєєв Г.В., Петерсон Л.Г.

Швидкий потяг затримався біля семафора на години і надолужив запізнення на 80-кілометровому перегоні, рухаючись зі швидкістю на 10км/год більшою, ніж передбачалася за розкладом. Яка швидкість потяга за розкладом?

Звичайно, учні 5-го класу не можуть  до кінця розв’язати таку задачу, але складання рівняння до неї дає позитивні результати при переході дітей до класу з поглибленим вивченням математики.

У 7-му класі, що навчається за програмою «Росток», велика увага приділяється перетворенням алгебраїчних виразів. Зупинимося на темі  «Формули скороченого множення». Крім стандартного набору формул учні вивчають формули різниця та сума  n -х степенів aⁿ-bⁿ, n є N; aⁿ+bⁿ, n=2k+1, k є N та формули бінома Ньютона. За допомогою цих формул діти розв’язують такі завдання:

1. Доведіть, що при будь-якому натуральному n значення виразу:

17ⁿ-1 кратне 16;

2. Розкладіть на множники многочлен  х³+3х²у+3ху²+2у³.
3. Розв’яжіть рівняння  (х+1)³-(х-1)³=8.

Аналогічні завдання розв’язуються  у 8-му класі з поглибленим вивченням математики. А так як діти вже знайомі з такими прикладами, то повторюють їх і краще засвоюють.

Наступна лінія у математиці за програмою «Росток» – це лінія теорії чисел,  в якій розглядається тема «Подільність чисел». Вона є логічним початком цієї ж теми з курсу поглибленої алгебри 8-го класу.  У 7-му класі учні знайомляться з такими поняттями як подільність націло та ділення з остачею для цілих чисел, вчаться знаходити найбільший спільний дільник двох натуральних чисел за алгоритмом Евкліда, вивчають зв'язок між найбільшим спільним дільником та найменшим спільним кратним, вивчають ознаки подільності на 4, 6, 7, 8, 11, 25. Наведу приклади завдань які є спільними як для 7-го так і для 8-го класів:

1. Число а кратне 5. Доведіть, що 8а 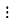40.
2. Доведіть, що
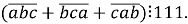
3. Розв’яжіть у цілих числах рівняння  9х²-у²=6.
4. Знайдіть неповну частку і остачу при діленні числа a на число b, якщо a=-26, b=3.
5. Знайдіть НСД чисел 253 і 299.
6. Яку остачу при діленні на 3 дає число виду 3р-2, де р – ціле число.
7. Доведіть, що для будь-якого  натуральногоn :

НСД(n;n+1)=1.

Наступна лінія у викладанні математики за програмою «Росток» - це курс «Основи теорії ймовірностей». Він виділений окремим предметом і включає розділи комбінаторика і теорія ймовірностей. Метою вивчення даного курсу в  6 -7-х класах виступає розвиток обчислювальних навичок учнів, ознайомлення з методами математичного моделювання, формування практичних вмінь і навичок. Значущість курсу обумовлена спрямованістю на формування наукового світогляду учнів й підкреслюється набутими знаннями і вміннями. Навчальний матеріал спецкурсу підібрано таким чином, щоб забезпечити розвиток креативності мислення дітей, підвищення рівня їх навчальної мотивації.  Вивчаючи предмет учні знайомляться з основними правилами комбінаторики, перестановками, розміщеннями, комбінаціями без повторень та з повтореннями, вивчають класичне , статистичне та геометричне поняття ймовірності, обчислюють ймовірність за допомогою правил комбінаторики. Це сприяє кращій роботі дітей у 9 класі з поглибленим вивченням математики, бо дані теми там також вивчаються і я у 7-му класі часто використовую підручник з алгебри для 9-го класу для класів з поглибленим вивченням математики, автори якого Мерзляк А.Г., Полонський В.Б., Якір М.С..

Однією з нетрадиційних ліній курсу є тема «Мова і логіка». Це виключно важливий матеріал для загального розвитку дітей. При вивченні даної теми вводяться поняття висловлювання, його істинності чи хибності, заперечення висловлювання, дається поняття контрприкладу.  Висловлювання поділяються на загальні та висловлювання про існування. Вводяться і активно використовуються для розв’язання різноманітних задач такі важливі поняття як «математична ідея», «гіпотеза», «математична проблема». Пояснюються поняття слідування та рівносильності, які широко використовуються  при поглибленому вивченні алгебри, коли вивчаються рівняння, нерівності та їх системи та геометричного матеріалу.

Остання лінія – геометрична. Я хочу більш детально зупинитися на ній, так як геометрія для учнів надзвичайно складна наука. Працюючи за програмою «Росток» не перший рік, я зрозуміла,що потрібно з молодших класів організувати інтелектуально-практичну і дослідницьку діяльність учнів направлену на розвиток та формування у них геометричного мислення.

За традиційною програмою основною задачею досистемного курсу геометрії є надання дітям певного об’єму  геометричних знань і вмінь, необхідних їм для нормального сприйняття оточуючого світу.

Наглядно-практична діяльність учнів широко використовується і в курсі математики за програмою «Росток», але тільки на перших етапах вивчення. Справа в тому,що геометрична лінія в цьому курсі тісно переплітається з однією із нетрадиційних тем для курсу математики в 5-6 класах темою «Мова і логіка», яка дозволяє знайомитися з геометричним матеріалом не тільки на наглядно-образному, а й на логічному рівні, що надзвичайно корисно для поглибленого вивчення геометрії.

Геометрична лінія містить такі етапи:

1. Знайомство з геометричними фігурами і поняттями на рівні уявлень;
2. Вивчення їх властивостей на рівні досліджень;
3. Висунення гіпотез;
4. Доведення гіпотез;
5. Використання одержаних знань на практиці.

Перші чотири пункти розглядаються у курсі математики 5-6-го класу, а з 7-го класу починається логічне доведення розглянутих раніше тверджень, яке продовжується при поглибленому вивченні предмета. При цьому створюється ситуація яка, крім підготовки мислення та практичних навичок, створює ситуацію, що забезпечує можливість позитивного відношення до подальшого вивчення систематичного курсу геометрії.

Наведу конкретні приклади вивчення геометричного матеріалу за підручником для 5-6 класів  автор Дорофєєв  Г.В., Петерсон Л.Г.. Геометричні знання буквально пронизують ці підручники і тісно переплітаються з розвитком логічної лінії курсу. Всі геометричні відомості про вивчені фігури діти записують у окремий зошит, який до переходу на поглиблений рівень містить дуже багато матеріалу.

Так у 5-му класі при вивченні теми «Мова і логіка» вводяться поняття прямокутного трикутника , катета та гіпотенузи. Учні самостійно висувають гіпотезу про знаходження площі прямокутного трикутника, а потім за її допомогою ми знаходимо площі інших видів трикутників, паралелограма, трапеції. При цьому діти за малюнками самостійно вказують які елементи даних фігур потрібно знати, щоб знайти їх площу.

При вивченні теми відношення у 6-му класі вводиться поняття синуса, косинуса, тангенса гострого кута прямокутного трикутника, та розв’язується вправа, в якій ми з учнями для конкретних прямокутних  трикутників за допомогою вимірювань знаходимо  синус, косинус і тангенс одного з кутів; обчислюємо суму квадратів синуса і косинуса цього кута; знаходимо відношення синуса до косинуса і порівнюємо його тангенсом даного кута; всі ці вправи виконуємо і для другого кута трикутника. Після виконання даної вправи учні  самостійно формулюють і записують перші тригонометричні формули, які з неї випливають. Так відбувається перше знайомство з тригонометрією . А вже у 8-му класі, коли ми поглиблено вивчаємо цей матеріал дітям дуже цікаво доводити дані формули, які колись були одержані практичним шляхом.

У темі розв’язування задач за допомогою пропорцій є вправа в якій вводиться поняття медіани трикутника. І діти за допомогою необхідних вимірювань висувають гіпотезу про поділ медіани точкою перетину у відношенні 2:1, рахуючи від вершини. Але я завжди наголошую, що це тільки гіпотеза, яка потребує доведення і буде доведена пізніше.

В кінці 6-го класу ми проводимо систематизацію геометричних знань, накопичених раніше. Першим у ній розглядається поняття означення. Ми вчимося означати поняття через раніше відомі, але я завжди звертаю увагу дітей, що  робити це до нескінченності неможливо. Далі розглядаю з учнями питання про поняття, які не мають означення та їх використання в означеннях. Кращим прикладом є означення відрізка і променя, де використовуються тільки не означувані поняття: «точка», «пряма». Зразу оговорюємо, що при складанні означень використовуємо загальні поняття, такі, як «лежати між», «з’єднувати», «частини», «протилежні» та багато інших.

Вправ, де потрібно назвати означуване поняття та вказати поняття на які воно спирається у підручнику  достатньо. Для  кожного з них будуємо логічні ланцюги  понять, які так чи інакше використовуються при введенні нового поняття.

Наприклад.                                      

                                                         Трикутник

                            Точка                       Пряма                    Відрізок

                                                                                    Точка           Пряма

Тому у старших класах я не витрачаю час на пояснення того, чим означення відрізняється від теорем та аксіом , значно економлячи час.

 У 6-му класі ми вивчаємо тему «Задачі на побудову». Серед завдань до цього пункту основними являються задачі на побудову трикутника за трьома сторонами, за двома сторонами і кутом між ними, за стороною і двома прилеглими кутами. Якщо це під силу учням, то побудову  супроводжуємо короткими математичними записами. Після виконання таких побудов учні висувають гіпотезу про рівність самих трикутників за рівними елементами, тобто ознаки рівності трикутників. Ми перевіряємо їх за побудовою, але я наголошую, що доведені вони будуть пізніше.

Велика увага  у підручнику 6-го класу за програмою «Росток» приділена просторовим фігурам: многогранникам і тілам обертання. Учні вчаться вірно їх малювати, робити моделі із різних розгорток, будувати перерізи многогранників площиною, а також розв’язувати задачі на знаходження площі поверхні та об’єму просторових фігур. Учні з великою цікавістю розв’язують такі задачі:

1. Чи вистачить дроту довжиною 1м, щоб зробити каркасну модель прямокутного паралелепіпеда з вимірами 7см, 9см, 14см?
2. Прямокутний аркуш паперу має розміри 12см і 8см. Чи вистачить цього аркушу, щоб обклеїти прямокутний паралелепіпед із вимірами 3см, 4см і 5см.

 Приходячи до класу з поглибленим вивченням математики учні, які навчалися за програмою «Росток» вже знайомі на наглядно-образному рівні знайомі з теоремою Піфагора, синусом, косинусом, тангенсом гострого кута прямокутного трикутника, з вписаним та центральним кутом, правильними многокутниками та многогранниками. Знають формули для обчислення площі трикутника і чотирикутника та формули площі поверхні і об’єму многогранників і тіл обертання. Вони орієнтуються у перетвореннях площин таких як  симетрія, паралельне перенесення, поворот. Починаючи з 8-го класу, ці поняття формуються  на логічному рівні за допомогою знайомих понять слідування та рівносильності, що полегшує засвоєння учнями складного геометричного матеріалу.

Отже, викладання математики за програмою «Росток» дає вчителю можливість:

- проводити навчання на високому рівні складності;
- розвивати здібність передбачати, висловлювати свої думки, ідеї та захищати їх;
- систематично створювати ситуації вибору для учнів і давати можливість здійснювати цей вибір;
- підвищити роль діалогічної форми навчання, як особливої взаємодії
повноцінного розуміння, що зумовлює поєднання зовнішнього і внутрішнього діалогу.

При цьому  істотно збільшується міцність знань і темп вивчення матеріалу без напруги для дітей. В подальшому, зазначене вище дуже позитивно впливає на роботу учнів у класах з поглибленим вивченням математики.

Література:

1. Алгебра : підруч. Для 9 кл. з поглибл. вивч. математики / А.Г.Мерзляк, В.Б.Полонський, М.С.Якір. – Х. : Гімназія, 2011. – 384 с.
2. Алгебра : підруч. Для 8 кл. з поглибл. вивч. математики / А.Г.Мерзляк, В.Б.Полонський, М.С.Якір. – Х. : Гімназія, 2009. – 386 с.
3. Математика 5, частина 1-4 : навчальне видання/ Г.В.Дорофєєв,  Л.Г.Петерсон . – Суми : ЗАТ «ІСА Інтерпапір», 2008.
4. Математика 6, частина 1-4 : навчальне видання/ Г.В.Дорофєєв,  Л.Г.Петерсон . – Суми : ЗАТ «ІСА Інтерпапір», 2009.