Відрізок. Довжина відрізка.

Урок № 7

Тема.  Розв'язування задач

Мета: розширити систему знань учнів про означення і способи зна­ходження НСД і НСК кількох чисел корисними властивостями НСД і НСК кількох чисел і вдосконалювати вміння знаходити НСД і НСК у різних випадках.

Тип уроку: застосування знань, умінь і навичок.

Хід уроку

I. Перевірка домашнього завдання

 Оскільки всі вправи домашньої роботи є аналогами завдань, що були виконані на попередньому уроці, на цьому етапі уроку мож­на зібрати зошити на перевірку.

II. Актуалізація опорних знань

Усні вправи

1. Обчисліть:

2. Серед записаних чисел 2; 7; 13; 15; 24; 30; 45 знайдіть ті, що:

а) є простими; б) є складеними; в) діляться на 3; г) діляться на 5.

3. Знайдіть НСК (a; b), НСД (а; b), якщо дано розклад а і b на прості множники: а) а = 2 · 3 · 5²; b = 3² · 5; б) а = 2³ · 5; b = 3 · 7².

III. Поглиблення знань учнів

 Основна мета уроку — це пропедевтика теми «Зведення дробів до найменшого спільного знаменника та скорочення дробів», тому на цьому уроці слід добре відпрацювати такі моменти:

а) знаходження НСК двох взаємно простих чисел та одну з ознак взаємно простих чисел;

б) знаходження НСК і НСД двох чисел, одне з яких ділиться на інше;

в) знаходження НСК двох чисел із властивості .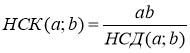

Для більш свідомого сприйняття матеріалу можна запропонувати уч­ням завдання, що допоможуть їм самим «відкрити» ці властивості.

1. Розкладіть на прості множники числа: а) 35 і 27; б) 24 і 25; в) 48 і 49.
   Знайдіть НСК і НСД цих чисел. Яку закономірність ви помітили?
2. Чи ділиться: а) 70 на 35; б) 144 на 36; в) 216 на 108? Розкладіть ці числа
   на прості множники і знайдіть їх НСК і НСД. Яку закономірність ви
   помітили?
3. Знайдіть НСК і НСД чисел: а) 20 і 60; б) 45 і 30; в) 24 і 25.
   Порівняйте добуток НСК і НСД кожної пари з добутком чисел кожної пари. Яку закономірність ви помітили?

Вочевидь більшість учнів зробить правильні припущення і вчителеві тільки залишиться сформулювати властивості НСК і НСД двох чисел і записати їх у вигляді конспекту 6.

IV. Відпрацювання навичок

 Перед початком розв'язування вправ учителю слід ще раз наголо­сити на тому, що відтепер до завдань на знаходження НСК і НСД треба ставитися більш свідомо, враховуючи моменти, зазначені в конспекті 6, а саме: чи не є числа взаємно простими (а такими без перевірки є або два простих числа, або два послідовних нату­ральних числа), чи не діляться одне на одне або чи не відомо якісь два компоненти з формули залежності між НСК і аb.

І рівень

Усні вправи

1. Знайдіть НСК і НСД чисел: а) 2 і 3; б) 2 і 4; в) 13 і 7; г) 25 і 5; д) 6 і 8.
2. Відомо, що НСД (a; b) = 3·5. Знайдіть НСК(a; b), якщо

а) аb = 105; б) ab = 45; в) аb = 165.

ІІ, ІІІ рівні

Письмові вправи

1. Уздовж дороги від пункту А до пункту В поставлено стовпи через кожні 45 м. Ці стовпи вирішили замінити іншими, поставити їх на відстані 60 м один від одного. Знайдіть відстань від пункту А до най­ближчого стовпа, який буде стояти на місці колишнього. (Яка най­менша може бути відстань між містами А і В?)
2. Тетяна купила в магазині яйця і поклала їх в невеличкий кошик. До­рогою вона збагнула, що кількість яєць ділиться на 2 і 3, і 5, і 10, і 15. Скільки яєць купила Тетяна? Чи правильним буде розв'язання: 2·3·5·10·15 = 4500 яєць? Як правильно розв'язати задачу?

IV. Підсумок уроку

Як рефлексію можна запропонувати тестові завдання.

VI. Домашнє завдання

Домашня самостійна робота № 1

Варіант 1

1°. Випишіть всі прості числа, які більші за 10 і менші за 20.

2°. Розкладіть на прості множники число 420.

3°. Знайдіть НСД (42, 56) і НСК (42, 56).

4°. Знайдіть розв'язок нерівності 25 < х < 35, який є спільним дільником чисел 52 і 78.

5. Яке найбільше двоцифрове число ділиться на 13?

Варіант 2

1°. Випишіть усі прості числа, які більші за 20 і менші за 30.

2°. Розкладіть на прості множники число 280.

3°. Знайдіть НСД (28, 42) і НСК (28, 42).

4°. Знайдіть розв'язок нерівності 10 < х < 25, який є спільним дільником чисел 52 і 84.

5. Яке найменше трицифрове число ділиться на 13?

6. Знайдіть суму всіх дільників числа 70.

Варіант 3

1°. Випишіть всі прості числа, які більші за 30 і менші за 40.

2°. Розкладіть на прості множники число 540.

3°. Знайдіть НСД (88, 121, 484) і НСК (88, 121, 484).

4°. Знайдіть розв'язки нерівності 100 < х < 200, кратні числам 9 і 21.

5. Яке найменше трицифрове число ділиться на 17?

6. Знайдіть суму всіх дільників числа 60.

Варіант 4

1°. Випишіть усі складені числа, які більші за 40 і менші за 50.

2°. Знайдіть розв'язки нерівності 90 < х < 190, кратні числам 8 і 14.

3°. На скільки НСК (42, 56, 70) більше за НСД (42, 56, 70)?

4°. Розкладіть на прості множники число 2200.

5. Яке найменше чотирицифрове число взаємно просте з числом 42?

6. Знайдіть суму всіх дільників числа 50.

Підготуватися до усного заліку. Запитання до заліку (див. с. 30)