Вправи і творчі завдання на уроках математики для розвитку креативних здібностей учнів

ОЗССО І-ІІІ ступенів с. Шрамківка

Золотоніського району Черкаської області

 

 

 

 

 

 

 

 

 

 

Доповідь на тему:

«Вправи і творчі завдання на уроках математики для розвитку

креативних здібностей учнів»

 

 

 

 

 

 

 

 

Учитель математики Сергієнко Л.І.

 

 

 

 

2023 р.

Наш час – це час суттєвих змін у науці, техніці,інформаційному середовищі, освіті. Суспільству потрібно люди, які здатні приймати нестандартні рішення, вміють творчо мислити. Як зазначено у Національній доктрині розвитку освіти, «Держава повинна забезпечувати розвиток творчих здібностей і навичок самостійного наукового пізнання, самоосвіти і самореалізації особистості». Одним із вирішальних чинників розв’язання цих завдань є розвиток креативного мислення учнів. Що ж таке креативність?

   Творчий                                                               Створення

За схемою бачимо, що термін «креативність» має подвійне значення: творчість і створення. Але треба пам’ятати, що творчість не завжди дає творчий результат, а креативність веде до створення творчого продукту.

Креативне навчання – це процес постійної співпраці вчителя та учня. Навчальний процес організовується як живий контакт партнерів, зацікавлених один у одному та в справі, якою вони займаються разом. Креативне навчання має характерну рису: навчальний процес зливається з життям, із рішенням реальних творчих задач.

Важливо, щоб учні розуміли, що творчість починається саме із сумніву. Дуже дієвим на уроках є створення проблемних ситуацій, формулювання проблемних питань, висування проблемно-пошукових гіпотез. Наприклад, під час вивчення теми «Сума кутів трикутника», щоб краще привернути увагу учнів до теореми, корисно провести деяку попередню роботу:

-         Спробуйте побудувати  трикутник, у якого кожен кут дорівнює 80º…

-         Один кут трикутника дорівнює 50º, другий - 100º. Чи зможете ви знайти градусну міру третього кута?..

-         Накресліть кожен у своєму зошиті якийсь трикутник. А тепер виміряйте всі три кути і знайдіть їхню суму…

У всіх трьох наведених випадках перед формуванням теореми створюється проблемна ситуація: ставляться запитання, на які учні поки що не можуть дати обґрунтованої відповіді. Звичайно, постановка таких питань привертає увагу учнів. Вони чекають на відповіді і тому максимально уважні.

Розгляд софізмів розвиває спостережливість, вдумливе і критичне ставлення до того, що вивчається,виховує в учнів критичне мислення.

Математичні софізми привчають ретельно стежити за точністю формулювань, правильністю записів і креслень при розв’язуванні задач. За допустимістю узагальнень. До того ж розгляд софізмів захоплюючий.

Так наприклад в 6 класі при вивченні теми «Ділення раціональних чисел» для зацікавлення учнів і розвитку в них логічного мислення використовується такий софізм:

Стверджується, що 5 = 6. Для доведення цього використовується числова рівність: 35 + 10 – 45 = 42 + 12 – 54. Отримаємо: 5(7 + 2 – 9) = 6(7 + 2 – 9). Поділимо обидві частини на спільний множник. Отримаємо 5 = 6. Де помилка?

Учні, які засвоїли, що на нуль ділити не можна дають відповідь на задане запитання.

При вивчені у 8 класі теми «Властивості арифметичного квадратного кореня» розглядаю такий софізм: Стверджую, що 2 = 3. Маємо: 4 – 10 = 9 – 15, 4 – 10 + 6 = 9 = 15 + 6, (2 - )² = (3 - )², 2 -   = 3 - . Отже 2 = 3. Де помилка?

Щоб розв’язати задачу, потрібно умову задачі перевести на мову алгебри. Мова алгебри – рівняння. «Щоб  вирішити питання, яке відноситься до чисел або до відношень величин, потрібно перекласти задачу з рідної мови на мову алгебри», писав великий Ньютон в своєму підручнику «Загальна арифметика». Як зробити переклад з рідної мови на мову алгебри, Ньютон показав на прикладах. Ось один із них:

На рідній мові	На мові алгебри
Купець мав деяку суму грошей.	х
За перший рік він витратив 100 фунтів.	х - 100
До грошей, що залишились, добавив їх третю частину	(х – 100) + =
За наступний рік він знову витратив 100 фунтів	– 100 =
І збільшив решту грошей на її третю частину.	+ =
За третій рік він знову витратив 100 фунтів	– 100 =
Після того як він добавив до решти її третю частину,	+ =
грошей у нього стало в двічі більше.	= 2х

Щоб знайти скільки грошей було в купця спочатку, потрібно лише розв’язати останнє рівняння.

Вправа «Не помились». На дошці записані такі числа: 6, 9, 8, 3, 7, 5, 2, 4. Учні, які сидять один за одним, повинні швидко дати відповідь від множення кожного із чисел, наприклад на 8.

Саме впровадження на уроці креативних, розвиваючих ігор може сприяти розвитку пізнавальної активності в школярів. Використання нетрадиційних уроків-ігор дає змогу практично застосовувати математичні зання дітей. Для цього вчителям необхідно володіти сучасними методами, які б пробуджували у школярів бажання пізнавати нове, незвідане. Хорошим доробком у цій справі будуть розвиваючі вправи та завдання. Набір дидактичних розвиваючих ігор, вправ, може сприяти розвитку різноманітних якостей і здібностей у дітей, для допомоги у тому, щоб проявляти і реалізовувати пізнавальну активність у процесі розкриття і засвоєння шкільного матеріалу.

Так, у своїй роботі на уроках я використовую систему запитань, створюючи різного роду ігрові ситуації або вносячи творчі елементи, завдяки чому учні отримають змогу активізувати розумову діяльність, робити висновки. Серед основних типів завдань такі:

1. Завдання з незформульованими запитаннями.

Приклад. Шоколад коштує 15 грн, коробка цукерок 30 грн. Вкажіть всі можливі питання за умовою завдання.

2. Завдання з відсутніми даними.

Приклад. З двох пунктів виїхати одночасно два автомобіля. Швидкість одного з них дорівнює 65 км/год, а швидкість іншого – на 7 км/год більша. Яка відстань буде між автобусами через 2 години?

Учням ставлю запитання: Чому не можна дати відповідь на запитання задачі?

Чого не вистачає? Що потрібно додати? Доведи. що тепер завдання точно можна буде вирішити? А можна що-небудь отримати навіть з наявних даних? Який висновок можна зробити з аналізу того, що дано?

3. Задачі із зайвими даними.

У 21 кг рису містить 16 кг крохмалю, а у 12 кг ячменю – 7 кг крохмалю. У магазин привезли 42 кг рису та 14 кг ячменю. Де крохмалю більше – в 1 кг рису чи в 1 кг ячменю?

4. Завдання з кількома розв’язками.

Приклад. За три дні в магазині продано 1280 кг яблук. У перший день продали 25% всіх яблук, а у другий день – 45% усіх яблук. Скільки кілограмів яблук продали в третій день? Розв’яжіть задачу кількома способами. Який з них найбільш простий.

 

5. Завдання зі зміною умови.

Приклад. Вихідна задача. Туристи пройшли за день 20 км, що склало 40% наміченого маршруту. яка довжина маршруту?

Другий варіант. Туристи пройшли за день 20 км і їм залишилося пройти 60% наміченого маршруту. Яка довжина маршруту?

6. Завдання на доведення.

Саме при виконанні доведень відточується логічне мислення учнів, розробляються логічні схеми розв’язування задач, виникає потреба в обґрунтуванні математичних фактів.

Приклад. Доведіть, що сума будь-яких двох послідовних непарних чисел ділиться на 4.

7. Завдання на логічне міркування, дослідження.

Для прикладу в 6 класі я задаю наступні задачі:

     Чи існують числа обернені самі собі. Скільки таких чисел? Назвіть їх. При яких значеннях а і b правильні:

а) Рівність а/b = 0; b = 1; а/b =-1.

б) Нерівності аb ˃1; а/b ˃1; а|b˂ -1.

Найважливішими математичними операціями є аналіз і синтез. Аналіз пов'язаний з виділенням елементів даного об’єкта, його ознак або властивостей. синтез – поєднання різних елементів, сторін об’єкта в єдине ціле. У розумової діяльності аналіз і синтез доповнюють один одного. Формуванню та розвитку даних від учнів вимагається проводити правильні міркування, розглядати об’єкти з різних сторін, вказувати їх різні властивості, а також постановка різних питань щодо даного об’єкта. Ось деякі завдання:

1. Як розрізати фігуру на три рівні частини?

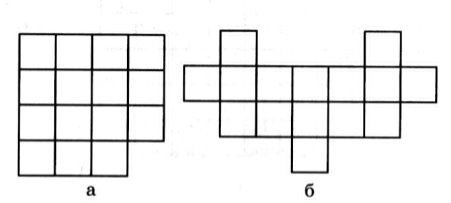
Відповідь:

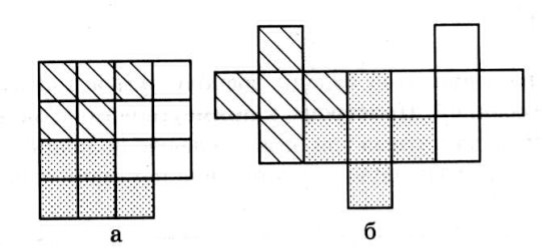
2. Скільки трикутників на малюнку?

 

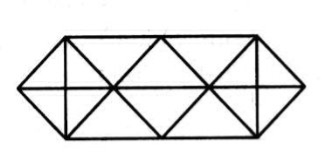
Відповідь: Всього 28 трикутників.

3. Який знак потрібно поставити між 2 і 3, щоб вийшло число більше за 2, але менше 3? (Відповідь: кому. 2,3.)

4. До царя Гороха дійшла чутка, що хтось з трьох богатирів убив Змія Горинича. Цар наказав усім трьом з’явитися до двору, і мовили вони:

Ілля Муромець : «Змія вбив Добриня Микитич».

Добриня Микитич: «Змія вбив Альоша Попович»

Альоша Попович: «Я вбив змія».

При цьому виявилося, що один з них сказав правду, а двоє злукавили. Хто вбив змія? (Відповідь: Змія вбив Добриня Микитич.)

5. Ліза, Галя і Ніна жили в різних будинках. Будинок № 1 – високий кам’яний, № 2 – високий дерев’яний, № 3 – невеликий кам’яний. В якому будинку жила кожна з дівчаток, якщо Галя і Ніна жили у високих, а Ніна і Ліза в кам’яних?  (Відповідь: Ніна жила в будинку № 1, Галя жила в будинку № 2, Ліза в будинку № 3.)

8. Завдання на вироблення фінансової грамотності.

У магазині є три види плитки для підлоги:

Вид плитки	Ціна однієї плитки
Квадратна плитка зі стороною 2 дм	24 грн
Плитка, що має довжину 2 дм і ширину 1 дм	13 грн
Квадратна плитка зі стороною 3 дм	50 грн

 

У кухні, довжина якої 6 м, а ширина 3 м, потрібно покрити підлогу плиткою. Яку плитку краще придбати, щоб затрати на покриття підлоги були найменші? Обчисліть ці витрати.