З досвіду роботи "Сучасний урок математики"
СУЧАСНИЙ УРОК МАТЕМАТИКИ
|
|
Супрунова Валентина Олексіївна вчитель математики КЗ «Лисичанська спеціалізована школа І-ІІІ ступенів № 27 Лисичанської міської ради Луганської області» |
Зміст
Вступ………………………………………………………………………………..3
РОЗДІЛ Ⅰ. Сучасний урок в системі освіти………………………………………5
- Поняття, особливості, вимоги сучасного уроку………..………………….5
- Типи і структура сучасного уроку………………………………………….10
РОЗДІЛ Ⅱ. Сучасний урок математики…..…………………………………….19
2.1. Включення в сучасний урок математики різних методів і технологій…....19
2.2 Розробка фрагменту уроку…………………………………………………….22
Висновки……………………………………………………………………………29
Література………………………………………………………………………….31
Вступ.
Наука, суспільство змінюються, набувають нові якості, реформи відбуваються у всіх сферах життя нашого суспільства, в тому числі і в освіті. В результаті, поняття сучасного уроку набуває нового змісту. Поняття «сучасний урок» знаходиться в постійній динаміці. Розвиток таких наук, як педагогіка, дидактика, методика, психологія веде до постійного удосконаленню поняття «сучасний урок», так як досягнення цих наук суттєво впливають і на сам урок.
В сучасних умовах відбувається усвідомлення цінності та практичної значущості освіти. У результаті цього значно зростають вимоги до якості освіти школярів. Учитель в таких умовах стоїть перед необхідністю удосконалення всіх сторін процесу навчання. Сучасний етап суспільного розвитку характеризується низкою особливостей, які висувають нові вимоги до шкільної освіти. Змінюються пріоритети й акценти в освіті, воно стає спрямованим на розвиток особистості, формування в учнів таких якостей і умінь, які в подальшому повинні дозволити йому самостійно вивчати що-небудь, освоювати нові види діяльності і, як наслідок, бути успішним у житті. Метою випускної кваліфікаційної роботи буде розгляд особливостей сучасного уроку, вимог до нього і вивчення впливу даних вимог до уроку на якість навчання математики.
Для досягнення мети поставимо перед собою такі завдання:
- Визначити поняття «сучасний урок».
- Розглянути особливості та ознаки сучасного уроку.
- Визначити вимоги до сучасного уроку.
- Розглянути включення різних методів і технологій в урок математики щоб він відповідав поняттю «сучасний урок математики».
- Показати на прикладі фрагменту уроку можливість включати нестандартні методи в структуру уроку.
Проблемою сучасного уроку займається багато вчених і педагогів. За основу в своїй роботі я взяла книги «Вимоги до сучасного уроку» Поташника М. М, «Сучасний урок. Інтерактивні технології навчання О. І. Пометун, «Теорія і технологія навчання математики в середній школі» під редакцією Т. А Іванової. У книзі Поташника М. М. на сучасній науковій основі викладено методичні вимоги до основної форми організації освітнього процесу - уроку в умовах розвитку школи. У посібнику також даються: розроблені з урахуванням нових вимог до сучасного уроку схема загальнодидактичного аналізу уроку, методика вивчення утруднень вчителів у підготовці та проведенні уроку та інші методичні матеріали для самоосвіти вчителя і організації методичної роботи в школі з проблеми освоєння нових вимог до уроку.
У посібнику О. І. Пометун розглядаються сучасні підходи до організації навчання, зокрема впровадження інтерактивних технологій. Обговорюється питання, як об'єднати різні моделі навчання, розглядається сучасний підхід до типології і структурі уроку.
У книзі Іванової Т. А проектується сучасна методична система навчання математики, методологічну основу якої складають концепції гуманітаризації освіти, особистісно-орієнтованої, компетентнісного, діяльнісного та технологічного підходів до навчання. З цих позицій аналізуються цілі загальної математичної освіти, їх конкретизація на рівні навчальної теми і окремого уроку; викладається технологія навчання основним дидактичним одиницям і побудова уроків різних типів, де учень виступає як суб'єкт навчальної діяльності; описується діагностика процесу навчання на всіх його етапах.
РОЗДІЛ Ⅰ. СУЧАСНИЙ УРОК В СИСТЕМІ ОСВІТИ.
- Поняття, особливості, вимоги сучасного уроку.
Почнемо ми з розгляду поняття і особливостей уроку .
Урок як форма організації навчальної роботи існує з 17 століття, тобто більше 350 років. Цей педагогічне винахід виявився настільки життєздатним, що і в наші дні урок залишається найпоширенішою формою навчально-виховного процесу в школі.
Урок - це така форма організації педагогічного процесу, при якому педагог протягом точно встановленого часу керує пізнавальною, колективною та іншою діяльністю постійної групи учнів (класу) з урахуванням особливостей кожного з них, використовуючи види, засоби і методи роботи, що створюють сприятливі умови для того, щоб всі учні оволоділи основами досліджуваного предмета безпосередньо в процесі навчання, а також для виховання і розвитку пізнавальних здібностей і духовних сил школяра.
За традиційним визначенням, урок - це така форма організації навчальних занять, при якій зберігаються тимчасові і локальні рамки, постійний складу учнів і певна дидактична організація.
Урок є частиною навчально-виховного процесу і на нього, як і на навчально-виховний процес, впливають:
-
зміни, що відбуваються в суспільстві;
- державне замовлення школі на підготовку майбутніх громадян, які можуть задовольнити актуальні потреби суспільства;
- державні стандарти і програми з їх цілями і предметним змістом;
- сучасні педагогічні концепції з їх цілями, принципами, технологіями навчання.
Крім даних умов на структуру і результативність уроку впливає особистість учителя, його стиль спілкування з учнями, рівень професійної підготовки, ступенів оволодіння методичними прийомами та вміння враховувати під час управління навчальною діяльністю, психологічні особливості кожного учня.
Сьогодні вітчизняні та зарубіжні вчені поряд з традиційним уроком виділяють ще й такі форми організації навчального процесу, як: інтегрований урок, лекційно-семінарські або лекційно-практичні заняття, проектні заняття, творчі майстерні, автономне навчання та самостійна робота учнів (Т. Тучкова). Кожен з цих типів занять має свої особливості в організації та змістовному наповненні.
Пошук нових типів уроків і нових форм організації навчальної діяльності учнів пов'язані з прагненням вчителів вирішити основні проблеми уроку, до яких відносять:
-
проблему, пов'язану з колективним способом організації навчання та індивідуальним характером сприйняття, інтелектуальною діяльністю, емоційного реагування та розвиток кожного учня;
- проблему, пов'язану з організацією прямого і зворотного зв'язку між учителем і учнями;
- проблему, яка виникає через суперечності між вербальним характером навчання та завданнями різнобічного розвитку дітей, здатних до творчого мислення;
- проблему, пов'язану з реальним обсягом конкретного навчального матеріалу, який необхідно засвоїти в рамках програми, часом, необхідним для його вивчення і тривалістю уроку.
Ступінь розуміння і вирішення цих проблем суттєво впливає на ефективність уроку.
Для сучасного уроку характерними ознаками є:
- Гуманітарний потенціал і гуманізація навчання;
- Варіативність і гнучкість структури уроку;
- Спрямованість уроку на особистість учня;
- Системний підхід до архітектури уроку і процесу навчання;
- Спрямованість уроку на головне - генералізація навчання;
- Повне засвоєння нового матеріалу на уроці;
- оптимізація форм роботи на уроці;
- економія часу в шкільному навчанні.
Сучасний урок - це урок демократичний. Він проводиться не для учнів, а разом з ними.
У результаті цього виникли різні технології навчання: адаптивна система навчання, технологія диференційного навчання, технологія модульного навчання, інформаційні технології навчання, технологія повного засвоєння знань, технологія колективного способу навчання, технологія інтегрованого уроку.
Залежно від цілей уроку виділяють освітні, виховні і розвиваючі вимоги до «сучасного уроку».
Освітні вимоги .
- Цілеспрямованість уроку;
- Раціоналізація і диференціація інформаційного наповнення уроку;
- Обґрунтований вибір засобів, методів і прийомів, орієнтований-них на навчання, розвивальне особу;
- Різноманітність форм організації навчальної діяльності учнів;
- Варіативний підхід до формування структури уроку;
- Реалізація на уроці в оптимальному співвідношенні всіх дидактичних принципів і правил з них випливають.
Виховні вимоги.
- Виявлення і використання на уроці виховних можливостей (зміст навчального матеріалу, методів навчання, форм організації у їх взаємодії; система відносин складаються на уроці).
- Чітка постановка виховних цілей та реалізація їх через систему виховних завдань.
Розвиваючі вимоги
- Розвиток умінь творчого характеру.
- Розвиток мовлення, мислення, пам'яті, сенсорної сфери, рухової сфери, пізнавального інтересу і допитливості.
- Формування і розвиток не тільки предметних, та й загально навчальних вмінь і навичок.
- Вивчення і облік рівня розвитку та психологічних особливостей учнів, проектування «зони найближчого розвитку».
- Проведення навчальних занять на «випереджаючому» рівні, стимулювання настання нових якісних змін у розвитку.
- Розвиток інтелектуальної, вольової, емоційної сфери особистості.
Існує й інша класифікація вимог до сучасного уроку.
Дидактичні вимоги до сучасного уроку:
- чітке формулювання освітніх завдань в цілому та їх складних елементів, їх зв'язок з розвиваючими і виховними завданнями;
- визначення оптимального змісту уроку відповідно до вимоги навчальної програми та цілями уроку, урахуванням рівня підготовки та підготовленості учнів;
- прогнозування рівня засвоєння учнями наукових знань, сформованості умінь і навичок як на уроці, так і на окремих його етапах;
- вибір найбільш раціональних методів, прийомів і засобів навчання, стимулювання і контролю, оптимального їх впливу на кожному етапі уроку, вибір, що забезпечує пізнавальну активність, поєднання різних форм колективної та індивідуальної роботи на уроці і максимальну самостійність у навчанні учнів;
- реалізація на уроці всіх дидактичних принципів;
- створення умов успішного навчання учнів.
Психологічні вимоги до сучасного уроку
- Проектування розвитку учнів у межах вивчення конкретного навчального предмета і конкретного уроку;
- Облік в цільовій настанові уроку психологічної задачі вивчення теми і результатів, досягнутих у попередній роботі;
- Передбачення окремих засобів психолого-педагогічного дії, методичних прийомів, що забезпечують розвиток учнів.
Гігієнічні вимоги до сучасного уроку
- температурний режим;
- фізико-хімічні властивості повітря (необхідність провітрювання);
- освітлення;
- попередження втоми і перевтоми;
- чергування видів діяльності;
- своєчасне та якісне проведення фізкультхвилинок;
- дотримання правильної робочої пози учня;
- відповідність класної меблів росту школяра.
Вимоги у техніці проведення уроку
- урок повинен бути емоційним, викликати інтерес до навчання і виховувати потребу в знаннях;
- темп і ритм уроку повинні бути оптимальними, дії вчителя та учнів завершеними;
- необхідний повний контакт у взаємодії вчителя та учнів на уроці повинні дотримуватися педагогічний такт і педагогічний оптимізм;
- домінувати повинна атмосфера доброзичливості і активної творчої праці;
- по можливості слід змінювати види діяльності учнів, оптимально поєднувати різні методи і прийоми навчання;
- забезпечити дотримання єдиного орфографічного режиму школи.
Реалізація запропонованої сукупності вимог до системи уроків забезпечить необхідний рівень організованості, а, отже, і якості уроку в сучасній школі.
Таким чином, сучасний урок складається з розуміння його, як цілісної системи при обліку типології і вимог до його підготовки і проведення.
Основною складовою успішного сучасного уроку я вважаю здатність вчителя до творчості. Адже якщо вчитель творчо підходить до уроку, то він і буде цікавим і не нудним.
Від того доброго, що дає педагог дітям, добро народжується в них самих. Він заряджає їх енергією, віддаючи частинку себе.
Ще не менш важливою складовою сучасного уроку є вміння вчителя критично аналізувати свій урок. Це дозволить вчителю удосконалювати свою майстерність, зробити уроки живими, що проходять в діалозі з дітьми.
Щоб точніше зрозуміти, яким має бути сучасний урок, необхідно розглянути типи і структури сучасного уроку.
- Типи і структура сучасного уроку.
Існує безліч авторів, які приводять різну типологію уроків. Розглянемо деякі з них.
Типологія уроків В. А. Онищука.
- Урок засвоєння нових знань;
- Урок освоєння нових умінь і навичок;
- Урок комплексного застосування знань;
- Урок узагальнення та систематизації знань;
- Урок перевірки, оцінки та корекції знань, умінь і навичок;
- Комбінований урок.
Система викладання Л.В. Махової:
- розповідь оглядового типу по всій темі;
- урок питань учнів вчителю і додаткових роз'яснень
- урок - практична робота;
- урок узагальнюючого типу з картками-завданнями, орієнтуючими на виділення і засвоєння головних елементів навчального матеріалу;
- заключне опитування з теоретичного матеріалу;
- рішення задач по темі із застосуванням мікрокалькуляторів.
Система уроків, запропонована Р.Г. Хазанкіним:
- урок-лекція по всій темі;
- уроки-вирішення ключових завдань;
- урок-консультація;
- урок-залік.
Кожен тип уроку має свою структуру. Наведемо деякі з них.
Структура уроку вивчення нового матеріалу:
- первинне введення матеріалу з урахуванням закономірностей пізнання при високій розумової активності учнів;
- вказівка на те, що учні повинні запам'ятати;
- мотивація запам'ятовування і тривалого збереження в пам'яті;
- повідомлення або актуалізація техніки запам'ятовування (робота з опорними для пам'яті матеріалами, смислове групування тощо);
- первинне закріплення під керівництвом вчителя за допомогою прямого повторення, часткових висновків;
- контроль результатів первинного запам'ятовування;
- регулярне систематизуючи повторення через короткі, а потім більш тривалі проміжки часу в поєднанні з різними вимогами до відтворення, у тому числі і з диференційованими завданнями;
- внутрішнє повторення і постійне застосування отриманих знань та навичок для придбання нових;
- часте включення опорного матеріалу для запам'ятовування в контроль знань, регулярна оцінка результатів запам'ятовування і застосування.
Структура уроку формування вмінь та навичок:
- постановка мети уроку;
- повторення сформованих умінь і навичок, які є опо рій;
- проведення перевірочних вправ;
- ознайомлення з новими вміннями, показ зразка формування;
- вправи на їх освоєння;
- вправи на їх закріплення;
- тренувальні вправи за зразком, алгоритмом, інструкції;
- вправи на перенесення в схожу ситуацію;
- вправи творчого характеру;
- підсумок уроку;
- завдання додому.
Структура уроку повторення:
- організація почала уроку;
- постановка освітніх, виховних, розвиваючих завдань;
- перевірка домашнього завдання, спрямованого на повторення основних понять, умовиводів, основоположних знань, умінь, способів діяльності (практичної і розумової). На попередньому уроці, знаючи про майбутній повторенні, потрібно підібрати відповідне домашнє завдання;
- підведення підсумків повторення, перевірка результатів навч-ної роботи на уроці;
- завдання додому.
Структура уроку перевірки знань:
- організація початку уроку. Тут необхідно створити спокійну, ділову обстановку;
- постановка завдання уроку. Учитель повідомляє учнів, який мате-ріал він перевірятиме або контролювати;
- виклад змісту контрольної або перевірочної роботи (за-дачі, приклади, диктант, твір або відповіді на питання і т.п.). Завдання по обсягу або ступеня труднощі повинні відповідати програмі і бути по-сильним для кожного учня.
- підведення підсумків уроку. Учитель вибирає гарні роботи учнів, аналізує допущені помилки інших робіт і організовує роботу над помилками (іноді на це іде наступний урок);
- визначення типових помилок і прогалин у знаннях і уміннях, а також шляхів їх усунення та вдосконалення знань і умінь.
Структура узагальнюючого уроку:
- організаційний момент;
- вступне слово вчителя, в якому він підкреслює значення матеріалу вивченої теми або тим, повідомляє мету і план уроку;
- виконання учнями індивідуально і колективно різного роду усних і письмових завдань узагальнюючого і систематизує характеру, що виробляють узагальнені понятійні знання на основі узагальнення фактів, явищ;
- перевірка виконання робіт, коректування (при необхідності);
- формулювання висновків з вивченого матеріалу;
- оцінка результатів уроку;
- підбиття підсумків;
- завдання додому (не завжди).
Структура комбінованого уроку (він, як правило, має дві або де-кілько дидактичних цілей):
- організація почала уроку;
- перевірка домашнього завдання, постановка мети уроку;
- підготовка учнів до сприйняття нового навчального матеріалу, тобто актуалізація знань і практичних, і розумових умінь;
- вивчення нового матеріалу, в т.ч. і пояснення;
- закріплення матеріалу, вивченого на даному уроці і раніше пройденого, пов'язаного з новим;
- узагальнення і систематизація знань і умінь, зв'язок нових з раніше отриманими і сформованими;
- підведення підсумків і результатів уроку;
- завдання додому;
- підготовка (попередня робота), необхідна учням для вивчення нової теми (не завжди).
Нетрадиційні типи уроків
рольові ігри; виконання казкового сюжету; урок фантазування; ділова гра; круглий стіл чи конференція; прес-конференція; урок відкритих думок; урок-змагання; вікторина; слідство ведуть знавці; аукціон знань; урок-диспут; урок-турнір; урок-еврика; чарівний конверт; міжпредметний інтегрований урок; урок-конкурс; урок творчості; математичний хокей; урок-спектакль; огляд знань; урок-гра; урок-залік; урок-подорож; урок-змагання; урок взаємонавчання; урок-сходження; урок-діалог; мозкова атака; урок-брифінг; актуальне інтерв'ю; імітаційно-рольове моделювання; моделювання мислення учнів; рольова ділова гра; урок-лекція: (проблемна лекція, лекція візуальна, лекція вдвох, лекція-прес-конференція, лекція-консультація, лекція-провокація, лекція-діалог)
У своїй роботі я хочу зупинитися на типах і структурах уроків розвивального навчання в системі Ельконіна-Давидова. На уроках, побудованих за цією системою учні почувають себе розкутіше, їм дається велика самостійність.
В системі Ельконіна- Давидова урок - поняття позачасове, він може займати від 10 до 40 хвилин. Кожен тип уроку є важливою ланкою у формуванні навчальної діяльності учнів.
«Актом навчальної діяльності можна назвати відрізок часу від постановки однієї навчальної задачі до наступної через систему проміжних тактичних завдань» (А. Б. Воронцов).
Зміст навчального матеріалу засвоюється учнями в процесі навчальної діяльності. Від того, яка ця діяльність, з яких навчальних дій вона складається, як ці частини між собою співвідносяться, тобто яка структура навчальної діяльності - від усього цього багато в чому залежить результат навчання, його розвиваюча і виховна роль. Ставлення дітей до власної діяльності визначається значною мірою тим, як вчитель організує їх навчальну діяльність, яка її структура і характер.
Психологічні дослідження навчальної діяльності показали: для того, щоб в учнів виробилося правильне ставлення до неї, змістовна її мотивація, потрібно навчальну діяльність будувати особливим чином. Перш за все, повинна відбуватися орієнтація на дослідний активний підхід у побудові уроку, пов'язаний з пошуком різноманітних шляхів вирішення поставлених навчальних, проблемних завдань з використанням різноманітних активних форм навчання. Головною орієнтацією на уроці повинні стати власні дії учнів. Особливого значення набуває зміцнення усіх боків вміння школяра вчитися, що забезпечує засвоєння всіх видів знань та їх застосування в нових умовах, самостійне виконання їм навчальних дій та самоконтролю, самостійний перехід від одного етапу навчальної роботи до іншого; включення учнів у спільну навчальну діяльність. Як же цього досягти? Відповідь на це питання можна знайти в теорії навчальної діяльності, розробленої В.В. Давидовим.
Розглянемо структуру уроку.
1 етап. Мотиваційний етап – ситуація успіху.
На даному етапі відбувається демонстрація того, що учні вже знають і вміють, тобто створення «ситуації успіху». Кожен учень в індивідуальному порядку виконує конкретно-практичну задачу і дає констатуючу оцінку своїх досягнень. Таким чином, учні переконуються у своєму успіху і показують його іншим.
2 етап. Ситуація «розриву» - етап постановки учбової задачі.
Учні стикаються з ситуацією (створює її вчитель), що суперечить раніше засвоєним і продемонстрованим способам дії. Завдання вчителя - в колективних формах оцінити ці способи як недостатні: виділити в задачі принципово нові умови, провести аналіз наявних в учнів засобів і способів дії стосовно нових умов і зафіксувати невідповідність умов завдання і наявних способів дії. Тільки в результаті такої оцінки може виникнути питання про ті умови, які представлені у цій проблемній ситуації і які раніше учнями не враховувалися, тобто про ті «секрети», розгадка яких дозволить перебудувати засвоєні раніше способи дії.
3 етап. Етап розв’язання учбової задачі – перетворення і аналіз умови задачі, моделювання виявлених відношень.
На наступному етапі рішення задачі учням необхідно перетворити і провести аналіз досліджуваного об'єкта. Сенс перетворення полягає в тому, що воно повинно дозволити встановити та оцінити ті умови, на облік яких спирається загальний спосіб дії і які не враховувалися учнями раніше. Правильно організований аналіз перетвореного об'єкта повинен привести учнів до встановлення ряду принципово нових властивостей досліджуваного об'єкта. Проведений аналіз дозволить учням зробити висновок щодо нового способу дії, який фіксується в класі у вигляді моделі.
4 етап. Етап розв’язання учбової задачі – опробування сконструйованої моделі для розв’язання конкретно-практичних задач.
Тепер відкритий учнями загальний спосіб дії і зафіксований у графіко-знакової моделі потребує колективної оцінки з точки зору його «правильності». Критерієм правильності знайденого способу є можливість вирішення з його допомогою конкретно-практичних завдань. На цьому етапі роботи розгортається поопераційний контроль учнів за роботою загального способу дії. Учням необхідно не просто «застосувати» знайдений спосіб у кожному окремому випадку, а проконтролювати відповідність встановлених операцій конкретних умов практичної задачі.
5 етап. Етап розв’язання часткових задач.
При вирішенні приватних завдань необхідно встановити відповідність фактично виконуваних операцій тих, які описані в моделі. На основі цього кожен учень констатує, правильно чи неправильно він діє, тобто йде оцінка свого способу дії з точки зору його відповідності правилу (моделі).
6 етап. Етап уточнення і конкретизації відкритого способу дії або вихід на нову учбову задачу.
Наступний етап роботи починається тоді, коли при виконанні чергового завдання, учні правильно застосовують всі операції (операційний контроль це підтверджує), а потрібний результат все-таки отримати не вдається і тоді виникає необхідність перевірки правильності самої моделі.
Розглянемо типи уроків і їх структури в системі розвивального навчання Ельконіна- Давидова.
І. Урок постановки учбової задачі
Структура уроку постановки учбової задачі:
- Створення ситуації успіху.
- Створення ситуації розриву.
- Фіксація місця розриву в знаково-символічній формі.
- Формулювання навчального завдання учнями і вчителем.
- Рефлексія.
ІІ. Урок розв’язання учбової задачі
Структура уроку розв’язання учбової задачі:
- Аналіз умов вирішення завдання.
- Власне рішення задачі, конструювання нового способу дії.
- Рефлексія.
ІІІ. Урок моделювання і перетворення моделі
Структура уроку моделювання
- Перетворення умови завдання.
- Власне моделювання.
- Перетворення моделі.
- Рефлексія.
ІV. Урок розв’язання часткових задач
Структура уроку розв’язання часткових задач:
- Аналіз умов вирішення приватного завдання.
- Власне рішення приватного завдання, відпрацювання способу дії.
- Рефлексія.
V. Урок контролю і оцінки
Структура уроку контролю і оцінки:
- Створення навчальної ситуації.
- Контроль і оцінка використання способу дії.
- Рефлексія.
Для того щоб створити сучасний урок необхідно використовувати різні технології: інтерактивні технології, інформаційні технології, елементи гри (особливо у дітей 5-6 класів), поєднувати роботу в групах з індивідуальною роботою учнів, розглядати історичні факти, відкривати красу математики як науки.
РОЗДІЛ Ⅱ. СУЧАСНИЙ УРОК МАТЕМАТИКИ.
- Включення в сучасний урок математики різних методів і технологій.
Сьогодні масової комп'ютеризації вимагають всі галузі суспільного життя. Тому навчання учнів у школі вже неможливо без використання інформаційно-комунікаційних технологій. Впровадження інноваційних технологій сприяє розвитку особистості та організації продуктивної диференціальної діяльності учнів під час проведення уроків математики.
На даному етапі, значна частина вчителів, вже активно використовує у своїй роботі комп'ютерні технології, тобто електронні засоби навчального призначення, які сприяють:
- збільшення обсягу досліджуваного матеріалу на конкретному уроці:
- забезпечення наочності теоретичного матеріалу;
- підвищення інтересу учнів навчально-виховним процесом;
- можливість творчо і практично застосовувати знання, уміння і навичок;
- можливість виконувати завдання не тільки під керівництвом вчителя, а й самостійно контролюючи свою діяльність.
Найбільш раціональним є використання комп'ютерних технологій під час викладання геометрії, оскільки учні мають можливість наочно побачити перетворення фігур (симетрію щодо точки, симетрію щодо прямий, перетворення гомотетії і подібності).
На прикладі теми з геометрії «Перетворення фігур» (9 клас) можна за допомогою мультимедійних засобів зробити урок барвистим, цікавим і продуктивним. Даний урок допоможе учням простежити динаміку змін розміщення фігур в результаті різних перетворень, поетапно перевірити правильність виконання запропонованих завдань. На даному уроці за допомогою презентації вчитель може продемонструвати кадри, які дадуть учням побачити симетрію в природі, архітектурі і життя (метелик, сніжинка, симетричні будинку). Дані відомості допоможуть розвивати інтерес до математики і почуття краси в математиці.
Сучасний процес реформування освіти вимагає забезпечення не тільки якості навчального процесу, а й модернізацію діагностичних, тематичних, семестрових та річних форм контролю і оцінювання рівня навчальних досягнень учнів.
Альтернативою традиційної перевірці знань є комп'ютерне тестування, яке може проводитися з урахуванням різних видів (поточне, тематичне, семестрове, річне) і форм (індивідуального або колективного) контролю, як інструмент оперативного контролю. Такий метод швидко, об'єктивно і ефективно діагностує результати навчальної діяльність учнів.
Пізнавальний інтерес в учнів викликають також інтегровані уроки математики. На даних уроках здійснюється об'єднання математики та економіки, математики і мистецтва, математики та географії, біології, історії, поезії, музики ...
Кожен вчитель знає, як складно пояснювати новий матеріал, привернути увагу учнів до складної теми, якщо вони прийшли втомлені після уроку фізкультури, або невгамовні після музики, або урок математики восьмий за розкладом ... Учитель спираючись на досвід і особливість класу, застосовує різні способи. Це може бути спокійне обговорення цікавого факту, а може емоційна гра або творче завдання. Тобто використання хвилинок відпочинку на різних етапах уроку дуже дієвий спосіб залучення уваги і зацікавленості учнів. Головна мета «відпочинку» - створити позитивну атмосферу уроку, активізувати пізнавальну діяльність учнів, стимулювати творчу роботу.
Завдання, вирішення яких пов'язане з пошуком нових ідей, відіграють важливу роль у розвитку учнів, оскільки розвивають сміливість мислення, змушують ламати певні психологічні бар'єри і підвищувати інтерес до вивчення математики. Розвинений інтелект необхідний будь-якій людині, в якій би галузі він не працював. За словами відомого математика і педагога Маркушевича, «Знання з часом забуваються, а розвиток залишається». До таких завдань можна віднести задачі про сірниках. Можна навести ряд завдань пов'язаних з пошуком нової ідеї:
- За допомогою двох цифр, записаних разом, складене натуральне число. Потім, цифру записану ліворуч, вилучили. У результаті число збільшилося. Як це могло статися? (нова ідея полягає у використанні римської нумерації).
- Обчислити найбільш раціональним способом:arctg1+arctg2+arctg3. (нова ідея складається у застосуванні малюнку).
Сучасний інноваційний підхід до навчання математики також передбачає побудова математичних моделей, інтеграцію знань різного рівня, декомпозицію складних завдань, з'єднання аналітичних і графічних методів вирішення, створення евристичних алгоритмів навчання, перетворення моделей рівнянь і нерівностей як процес їх вирішення.
Наведені підходи дозволяють розвивати творчість учнів.
Для здійснення особистісно розвиваючого підходу в математиці існує ряд загальновідомих методів навчання: проблемний, дослідницький, організація учбового (конструктивного) діалогу учнів між собою за участю вчителя управлінця і організатора. Характерною особливістю є те, що типові завдання створюються і відбираються самими учнями, а контроль і змістовна оцінка правильності рішення здійснюється як з боку вчителя, так і самими учнями.
Залежно від рівня засвоєння матеріалу вчитель організує колекторні, колективно розподільні (групові, парні) і індивідуальні форми навчальної роботи. Дані види роботи є елементами інтерактивної технології.
Ще однією ознакою сучасного уроку є використання історичних довідок підготовленими дітьми під керівництвом вчителя.
Для того щоб урок математики став сучасним необхідне застосування різних навчальних технологій, методів, особистісно-зорієнтованого підходу до учнів, більшої самостійності учнів. Необхідно розвивати пізнавальний інтерес до математики і доводити необхідність математики в різних галузях життя.
2.1 Розробка уроку по темі «Пропорція» 6 клас.
Для узагальнення поняття сучасний урок я пропоную розглянути розробку уроку, який я спробувала побудувати за критеріями сучасного уроку.
Тема: Пропорція. Основні властивості пропорції.
Цілі:
навчальна: 1) ввести поняття пропорції; 2) вивести основні властивості; 3) закріпити нові поняття; 4) формувати вміння застосовувати властивості пропорції при вирішенні завдань.
розвиваюча: 1) прищеплювати кожному учневі смак до самостійної, активної творчої діяльності; 2) розвивати пізнавальний інтерес до предмета.
Виховна: 1) виховувати чесність в оцінці своїх знань; 2) навчати працьовитості, акуратності
Тип уроку: творча лабораторія
Методи: дослідження
Обладнання: дошка, підручник, карти настрою, опорні схеми по темі для кожного учня. Комп'ютерна презентація.
Структура уроку.
- Організаційний етап (5 хв)
- Пояснення нового матеріалу. (27 хв)
- Фізкультхвилинка (3 хв)
- Застосування поняття пропорція в повсякденному житті. ( 5 хв)
- Підведення підсумків. ( 3 хв)
- Повідомлення домашнього завдання (2 хв)
Хід уроку.
- Організаційний етап.( 5 хв)
- Девізом сьогоднішнього уроку будуть слова "Без борошна немає науки".
- Хтось сьогодні буде задоволений, що зумів вирішити сам або за допомогою однокласників смішне або важке завдання; хтось тим, що він дізнався щось нове; а хтось тим, що йому пощастило, і не довелося думати над завданням.
Перед вами листок настрою

Ви мій настрій бачите, він залежить від вас, від ваших знань. А який ваш настрій? Покажіть його, закрасивши синім олівцем те личко, яке відповідає вашому настрою до початку уроку.
- А тепер розгадайте ребус (картинка на дошці)

- Отже, ми сьогодні будемо говорити про пропорції, і її властивості.
- Учитель. Сьогодні в кабінеті математики відкрито науково-дослідницький інститут. Директором НДІ призначили мене, а всі ви - його наукові співробітники. Організовано три лабораторії, в кожній лабораторії я призначаю старшого наукового співробітника. (Видаю таблички «лабораторія №1, №2, № 3» та бейджики «старший науковий співробітник»), вони відповідають за злагоджену роботу всієї лабораторії.
- Пояснення нового матеріалу (27 хв)
Лабораторія № 1
Відомо, що результат при діленні називається часткою. Проте, нерідко для позначення цього результату використовується слово ... Вирішіть приклади, використовуючи відповіді, дізнайтеся це слово.
2,1 · ![]() = ш
= ш ![]() : 1
: 1![]() = о
= о
3,5 · ![]() = н
= н ![]() = я
= я
4,8 ·![]() = в
= в ![]() : 2 = ц
: 2 = ц
2,4 : ![]() = д 0,5
= д 0,5 ![]()
![]() = р
= р
4![]() : 9 – 4
: 9 – 4 ![]() ·
· ![]() = і
= і 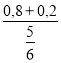 = п
= п
![]() :3 – 0,2 = е
:3 – 0,2 = е ![]()
|
1,8 |
0 |
12 |
1 |
0,5 |
0,7 |
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
Лабораторія № 2
Вирішіть приклади (ті ж, що і у лабораторії №1), заповніть таблицю і дізнайся, що в математиці, при вирішенні деяких завдань, доводиться мати справу з рівністю двох ...
Лабораторія № 3
|
1,8 |
0 |
12 |
1 |
0,5 |
0,7 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
Дізнайтеся, як називається рівність двох відношень, вирішивши приклади (ті ж, що і у лабораторії № 1), заповнивши таблицю.
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
Учитель. Давайте вислухаємо звіти лабораторій про виконану роботу.. Зі звітів лабораторій дайте відповідь на питання «що таке пропорція?» (Пропорція - це рівність двох відношень) Вирішимо усно задачу.
Чіп і Дейл купили сир. Чіп заплатив 100 грн. за 2 кг., А Дейл - 150 грн. за 3 кг. того ж сиру. З'ясуйте: «За однакової ціною був куплений сир?»
Учитель записує на дошці:
100 : 2 = 50 (грн.) – чип заплатив за 1 кг.
150 : 3 = 50 (грн.) – Дейл заплатив за 1 кг.
Отримали: 100 : 2 =150 : 3 або запишем по-іншому ![]() =
= ![]() .
.
Ми склали з вами пропорцію.
Запишемо рівність двох відношень в загальному вигляді a : в = с : d ; ![]() =
= ![]()
читається: а, поділене на в, дорівнює с, поділене на d, або відношення а і в дорівнює відношенню с і d, або а відноситься до в як d відноситься до с.
Числа а, в, с, d називають членами пропорції.
Подивіться на опорну схему яка знаходиться у кожного на столі.
Усно. Назвіть крайні і середні члени пропорції 100 : 2 = 150 : 3.
Учитель. А зараз послухаємо історичну довідку, підготовлену нашим співробітником.
Історична довідка о виникненні пропорції.
Учитель. А зараз проведемо справжню дослідницьку роботу, адже ми НДІ. Лабораторії отримують завдання.
Лабораторія № 1
Дана пропорція 3 : 4 = 9 : 12
1) Поміняйте місцями крайні члени. Чи буде отримана пропорція вірною?
2) Придумайте вірну пропорцію самі. Переконайтеся в цьому ще раз. Зробіть висновок.
3) Знайдіть добуток крайніх і середніх членів всіх пропорцій. Зробіть висновок.
Лабораторія № 2
1) Поміняйте місцями середні члени пропорції 3: 4 = 9: 12. Чи буде отримана пропорція вірною?
2) Придумайте вірну пропорцію самі. Переконайтеся в цьому ще раз. Зробіть висновок.
3) Знайдіть добуток крайніх і середніх членів всіх пропорцій. Зробіть висновок.
Лабораторія № 3
1) Поміняйте місцями крайні і середні члени пропорції 3: 4 = 9: 12. Чи буде отримана пропорція вірною?
2) Придумайте вірну пропорцію. Переконайтеся в цьому ще раз.
3) Знайдіть добуток крайніх і середніх членів всіх пропорцій. Зробіть висновок.
Учитель. Послухаємо звіт лабораторій про виконану роботу, зробимо висновки. (Заслуховуються звіти кожній лабораторії) Потім вчитель підводить підсумок і формулює властивість пропорції і робить запис на дошці:
3. Фізкультхвилинка (3 хв)
4. Застосування поняття пропорція в повсякденному житті. (5 хв)
Пропорції зустрічаються в навколишньому світі. Ще в давнину, спостерігаючи за навколишньою природою і створюючи твори мистецтва, люди шукали закономірності, які дозволяли б визначити прекрасне, тобто намагались вивести формулу краси. Естетичну насолоду, одержуване людиною при спостереженні досконалих форм, пояснюється «божественним відношенням» або «золотим перетином». Дотримання певних відносин в природі, мистецтві, архітектурі означає дотримання певних відносин між розмірами окремих частин рослини, скульптури, будівлі. «Золотий перетин» було критерієм гармонії та краси.
Так що ж таке «золотий перетин»? «Золотим перетином» називається поділ відрізка, при якому довжина всього відрізка так відноситься до довжини його більшої частини, як довжина більшої частини до меншої.
![]() Число, рівне відповідним відносинам, називають коефіцієнтом «золотого перетину» і наближене значення цього числа з точністю до десятих часток одно 0,6.
Число, рівне відповідним відносинам, називають коефіцієнтом «золотого перетину» і наближене значення цього числа з точністю до десятих часток одно 0,6.
Золотий перетин в соборі "Паризької Богоматері (Нотр-дам де Парі)".

Собор «Нотр-дам де Парі» у Парижі, Франція.
У багатьох метеликів співвідношення розмірів грудної та черевної частини тіла відповідає золотої пропорції. Склавши крила, нічний метелик утворює правильний рівносторонній трикутник. Але варто розвести крила, і ви побачите той же принцип членування тіла на 2,3,5,8. Бабка також створена за законами золотої пропорції: відношення довжин хвоста і корпусу дорівнює відношенню загальної довжини до довжини хвоста.

Наш сучасник, американський хірург Стівен Марквардт створив, використовуючи принципи золотого перетину, геометричну маску, яка може служити еталоном прекрасного особи.

Висновки
Висновки
Для даної випускної роботи була поставлена єдина мета - розглянути особливості сучасного уроку, вимоги до нього і вивчити вплив даних вимог до уроку на якість навчання математики.
Дана тема була обрана у зв'язку з особливою актуальністю даного питання в цей час, так як урок - це динамічне явище, постійно змінюється у зв'язку зі змінами та нововведеннями в дидактиці, психології, педагогіці, методики.
У роботі були дані різні визначення уроку. Але так як в літературі по-різному визначають це поняття, то були виділені загальні ознаки поняття «урок».
У педагогіці не існує строгого визначення поняття «сучасний урок». Однак, в роботі було дано визначення поняття сучасний урок, через виділення істотних ознак цього поняття.
Також в роботі були розглянуті основні характеристики сучасного уроку (завдання, цілі, функції уроку, вимоги до уроку). Приділялася увага типології і структурі уроку. Я зробила акцент на типології і структурі уроку в розвиваючому навчанні, так як вважаю, що дана система дає більше можливостей для творчості. Такий підхід дозволив описати урок найбільш цілісно, зачепити для розгляду всі елементи сучасного уроку.
У випускній роботі був описаний практичний приклад (у вигляді фрагмента уроку), який допоміг оцінити можливості вчителя у підготовці до сучасного уроку.
Зробимо основні висновки за виконану роботу:
1. Сучасний урок - одне з найбільш складних понять сучасної педагогіки. Складність його в тому, що зміни в суспільстві, деяких науках (дидактика, психологія, педагогіка) істотно впливають на урок, приводячи до змін парадигми уроку.
2. Велике значення сучасного уроку не тільки в освіті особистості, а й у розвитку кожної особистості, вихованні особистості.
3. Відбувається постійне вдосконалення уроку математики в напрямку вимог до сучасного уроку.
Література
1.Аліна Семененко. Комп'ютерне тестування як метод контролю рівня навчальних досягнень учнів.// Математика в школі.-2009.-№5.- с. 13-17.
2. Гадяцький М.В., Хлєбнікова Т.М. Організація навчального процесу в сучасній школі. - Харків: Видавництво "Ранок", "Векста". - 2004. -
136 с.
3. Иванова Т. А., Перевощикова Е. Н., Кузнецова Л. И. Григорьева Т. П. Теория и технология обучения математики в средней школе: Учебное пособие / Под ред. Т. А. Ивановой – Н. Новгород: НГПУ , 2009-355 с.
4. Канаржевский Ю.А. Анализ урока. — М.: Центр «Педагогический поиск»,-2000-336с.
5. Колеснікова Л. В., Мельникова Н. М. Інноваційні комп’ютерні технології в практичній діяльності вчителя математики.// Математика в школах України. -2012.- №1-2.- с.2-4
6. Олександр Курченко, Катерина Ребець. Математичні моделі: прикладні та між предметні зв’язки // Математика в школі .-2008. - № 6. – с.43-46.
7. Поташник М. М. Требования к современному уроку: [методическое пособие]/Поташник М. М. – М.:Центр педагогического образования, 2007-272 с.
8. Сучасний урок. Інтерактивні технології навчання: Наук.-метод. посіб./О. І. Пометун, Л. В. Пироженко. За ред. О. І. Пометун.-К: Видавництво А. С. К., 2004-192с.
9. Шарко В.Д. Сучасний урок. Технологічний аспект. - К., 2006 -218 с.
1
-
-
Щиро дякую!
-


про публікацію авторської розробки
Додати розробку
