Задачі на побудову лише циркулем

Задачі на побудову лише циркулем

У цій статті ми в доступній формі розглянемо теоретичні принципи сучасної теорії геометричних побудов і під цим кутом зору дамо методичний ескіз деяких методів геометричних побудов.

Задачі на побудову зародилися ще в античні часи, проте в окрему галузь абстрактної математики відокремилися значно пізніше.

Теорія задач на побудову відображає особливості і властивості графічної практики і показує шляхи її удосконалення та розвитку.

Як правило, задачі на побудову виконують циркулем і лінійкою (односторонньою).

  Є різні типи геометричних побудов, зокрема :

1. За допомогою лінійки(з однією робочою стороною);
2. Побудова лише циркулем;
3. За допомогою лінійки з вдома паралельними краями без шкали;
4. За допомогою геометричної лінійки і циркуля;
5. За допомогою рухомого прямого кута;
6. За допомогою довільного рухомого кута;
7. За допомогою циркуля і сталого відрізка;
8. За допомогою бісектора, приладу, який ділить кут навпіл;
9. Побудова 3-го і 4-го степенів, які виконують за допомогою різних кривих;

10) Побудова за допомогою інших засобів.

Проте найбільш поширеним у школі є побудова за допомогою циркуля і односторонньої лінійки.

 Циркуль і лінійку використовували ще в античні часи. Задачі на побудову розглядались у «Началах» Евкліда, проте Евклід ніде не згадує про лінійку і циркуль, і не показує, де побудовані задачі можуть застосовуватися.

Теорію розв’язування задач на побудову було розроблено лише в XIX ст., коли точно було визначено клас задач, які розв’язують за допомогою цих інструментів.

 Багато тисячоліть існують три класичні задачі на побудову, які не розв’язані ще донині. Це квадратура круга, трисекція кута і делійська (правильно делоська) задача (подвоєння куба).

 Великий інтерес у математиків  викликали задачі на побудову правильних многокутників. Цими питаннями займалися Гаусс, Шуберт, Гермес і Ейлер.

 Теорію задач на побудову лише циркулем розвинув датський математик Георг Мор (1640 – 1697), потім італійський математик Лоренцо Маскероні (1750 - 1800), а пізніше австрійський математик А. Адлер, який в 1890 р. довів, що будь-яка задача на побудову, яка розв’язується циркулем і лінійкою, може бути розв’язана лише циркулем.

 Геометрію лінійки (побудову задач лише лінійкою) розвивали Ламберт, Бріаншон і Понсоле. Найповніше розробив геометрію лінійки Штаудт (Ньюрберг, 1847 р.)

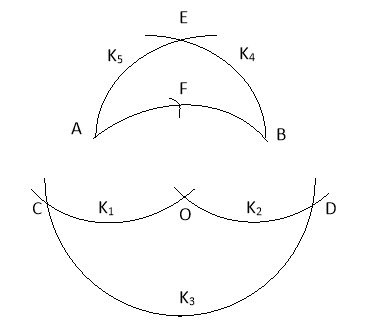 Розглянемо ряд задач на побудову лише циркулем.

№ 1

 Поділити навпіл дугу кола.

(Центр кола відомий).

 

 

 

 

 

 

Будуємо радіусом ОА кола К₁ і К₂ з центрами А і В. Радіусом АВ коло К₃ з центром О і радіусом СВ, кола К₄ і К₅ з центрами C і D; радіусом ОЕ коло з центром C або D (CE=DE=CB=DA).  Воно перетне дугу АВ в шуканій точці F.

 

 

 

 

 

 

 Доведення.

Чотирикутник ABDO – паралелограм, оскільки AB = OD i OA = BD, тому AB || OD. Аналогічно чотирикутник ABOC – паралелограм, тому  AB || OС. Оскільки відрізки OD i OC паралельні АВ, то точки С, О і D лежать на прямій, яка паралельна прямій АВ. Пряма ОЕ – вісь симетрій трапеції CABD, тому відрізок ОЕ ділить меншу основу АВ навпіл і ОЕ АВ. Точки А і В симетричні відносно прямої ОЕ, тому AF  дузі FB.

 Доведемо, що CF = OE.

 Нехай АВ = 2а. Проведемо ВН ⊥ ОD.

З ОВН( Н = 90):ВН² = R² – a²;

З СВН ( Н = 90): СВ² = 9а² + R² – a² = 8a² + R²;

CB² = CE²;

З  Δ СОЕ ( О = 90): ОЕ² =8a² + R²-4а²=4a² + R²

З  Δ СОF ( О = 90): CF² = 4a² + R².

 Бачимо, що ОЕ² = СF², тому ОЕ = СF.

 Такий спосіб поділу дуги навпіл показав Маскероні. Він буде використовуватись у багатьох наступних задачах.

№ 2

Поділити коло навпіл ;

№ 3

Поділити коло на три рівні частини.

№ 4

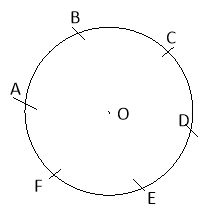Поділити коло на шість рівних частин (Центр О кола  відомий)

 

 

 

 

 

AB=BC=DC=DE=EF=AF=OA, тому дуга AD – половина кола, дуга АС – третина кола, дуга АВ – шоста третина.

№ 5

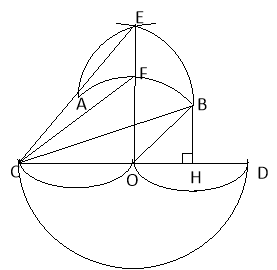
Поділити коло на чотири рівні частини (центр кола О відомий)

 

 

 

 

 

 

 На колі з центром О і радіусом R беремо довільну точку D. Шукаємо точки А і В на відстані радіуса від точки D. Потім будуємо кола з центрами у точках А і В і радіусом АВ. Нарешті будуємо кола з центрами у точках О і С і радіусом АВ. Відрізок DP – шуканий.

DP=DM=DK=MN=NK.

Доведення:

Пряма РЕ, яка проходить через точку D є дотичною до кола. З Δ ОDР

(D = 90, ОD = R, ОР=AB=a₃=R)

DP = =R, а це є сторона квадрата вписаного у коло радіуса R.

№ 6

Поділити коло на п’ять рівних частин. (Центр кола відомий)

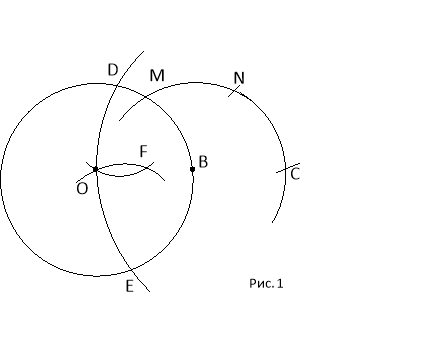 Спочатку покажемо, як за допомогою лише циркуля поділити відрізок ОВ на дві рівні частини.

 

 

 

 

 

 

Будуємо коло з центром О і радіусом ОВ. Потім будуємо коло з центром В і радіусом ОВ. Маємо точку М. Від точки М послідовно відкладаємо відрізки MN = NC=ОВ. Точки О, В і С лежать на одній прямій.

Будуємо коло з центром С і радіусом ОС. Одержали точки D і Е. З точок D і Е, як з центрів будуємо кола з радіусом ОВ, які перетнуться у точках О і F. Точка F лежить на прямій ОС, оскільки побудовані фігури симетричні відносно прямої ОС.

 Рівнобедрені трикутники ОDF і OCD подібні, оскільки вони мають спільний кут при основі,  Тому ;

OF = = = .

Тепер виконаємо поділ кола на 5 рівних частин.

 

 

 

 

 

 

 

 

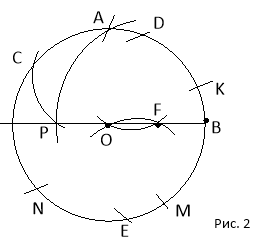
 Точка F ділить відрізок ОВ навпіл. АВ є сторона квадратна. Точку А можна побудувати (див. задачу № 5)

Будуємо коло з центром у точці F і радіусом FA, яке перетне діаметр кола (лише в цьому випадку ми використаємо лінійку для побудови діаметра) у точці Р. Відрізок АР є стороною правильного п’ятикутника вписаного у коло з радіусом R.

AC=CN=NM=MF=AK=AP.

Доведення:

З AOF ( О = 90): AF = ;

AF = FP, тоді РО = - = ;

З AOP ( О = 90): AP = = . (1)

 Відомо, що сторона правильного n-кутника вписаного в коло виражається за формулою а_n= 2R∙sin;

Тоді а₅ = 2R∙sin36;

Введемо позначення 18 = α, тоді sin36 = sin2α;

Sin36=cos54, або sin2α = cos3α;

2sinα∙cosα= 4 cos³α- 3cosα.

Оскільки cosα0, то поділимо обидві частини рівняння на cosα

4cos²α – 2sinα – 3 = 0, або

4sin²α + 2sinα – 1 = 0

sin α = – не задовольняє.

sin α =

cos α = = = ;

sin 2α = 22 ∙ ∙ = .

а₅ = 2R ∙ = (2)

З рівностей (1) і (2) маємо а₅ = AP.

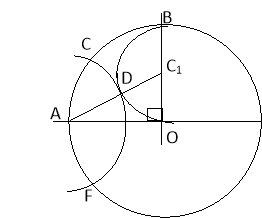Поділимо коло на п’ять рівних частин іншим способом (з використанням лінійки)

 

 

 

 

 

 Відрізок ОВ точкою С₁ ділимо навпіл. Будуємо коло з центром С₁ і радіусом . Проводимо ОА перпендикулярно ОВ. Будуємо відрізок АС₁, який перетинає коло в точці D. Потім будуємо коло з центром А і радіусом АD, яке перетне дане коло у точках С і F. Відрізок CF – сторона правильного п’ятикутника, вписаного в коло. Тоді відрізок АС буде стороною правильного десятикутника. Справді а ₁₀ = 2Rsin18.

 Раніше було доведено, що sin 18 = .

а ₁₀ = (- 1). (1)

З іншого боку з трикутника AOC (О = 90 ): AC = ;

AD = - = (- 1). (2)

З рівностей (1) і (2) випливає, що а ₁₀ = AD.

 Як бачимо, поділ кола на 5 рівних частин є не простою справою. Древні греки вміли будувати правильний n-кутники, де n = 3; 4; 5; 6; 8; 10, проте побудувати правильний 7-микутник і 9-тикутник їм не вдалося. Цю проблему більше двох тисяч років ніхто не міг вирішити. Лише в 1796 р. великий німецький математик К.Ф.Гаусс (його називали королем математики) зміг довести, що за допомогою циркуля і лінійки побудувати правильні 7-кутники і 9-кутники неможливо. Він довів, що це можна зробити лише тоді, коли число сторін правильного n-кутника має вигляд: n = 2^k, де kN і K>1, або

n  = 2^m∙p₁∙p₂∙…∙p_k, де p₁,p₂,…,p_{k –} різні гаусові числа, тобто числа виду + 1 (k – нуль, або натуральне число). Справді числа 7 і 9 не можна подати у вигляді + 1.

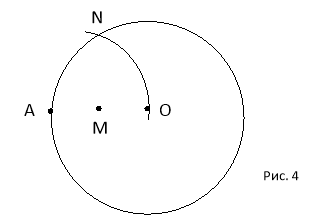 Покажемо, як сьогодні, з досить великою точністю, можна поділити коло на 7 рівних частин.

 

 

 

 

 

 Будуємо коло з центром А і радіусом ОА. Маємо точку N. Відрізок ОА точкою М ділимо навпіл (див. задачу №6). Відрізок MN є стороною правильного 7-кутника. ∆ ANO – рівносторонній зі стороною R, відрізок MN – його висота. MN = 0,8660R. (1)

 Використовуючи формулу сторони правильного n-кутника маємо,

а _{7 =} 2R∙sin = 2R∙sin 0,8670R (2)

 Ми розглянули основні способи поділу кола на рівну кількість частин за допомогою циркуля. На практиці потреба ділити коло на довільне число рівних частин буває набагато складнішою від уже запропонованих . У підручнику «Креслення», автор В.К.Сидоренко, в-во «Оріяна-Нова», Львів, 2004 на стор. 65 читаємо : « На рисунку зображено диск. Щоб побудувати контур його зображення, слід виконати поділ кола на 32 рівні частини. Здійснити графічним способом такий поділ неможливо (через його відсутність). Це невірно, оскільки 32 = 2⁵. Такий поділ можна зробити навіть одним циркулем.

 Коли виконують технічне креслення, то поділ кола на довільну рівну кількість частин виконують за допомогою таблиці хорд. Він ґрунтується на тому, що для поділу необхідно знати розхил циркуля, за допомогою якого на колі слід наносити поділки. Довжина хорди l, яку відкладають на заданому колі, визначають за формулою l = d∙k (d – діаметр кола, k – величина коефіцієнта, що відповідає заданому числу рівних частин на колі, яку можна задати з будь-якою наперед заданою точністю)

  По таблиці хорд

а ₇ = l 2R ∙ 0,43488 0,8698R (3)

 Бачимо, що сторона правильного семикутника, вписаного в коло, виражається різними величинами, (1), (2), (3), проте найбільш точне значення (2)

а ₇ 0,8670R, тому що sin обчислювалося з точністю до 0,0001 за допомогою ряда Маклорена для функції sin x = x - + - + … + (-1)^n-1 ∙ + …

 Задачі на побудову правильних многокутників при n = 9;11;13;… будуть розглянуті пізніше.