Задачі з астрономії (частина ІII)

Задачі з астрономіїЧастина ІІI Небесна сфера

Теоретичні відомості Небесна сфера

Небесна сфера (лат. orbis coelestis)— уявна сфера довільного радіуса, на яку проєктуються небесні тіла.

Z - зеніт. Z’ - надир. Площина горизонту. N – точка півночіS – точка півдня. Р – північний полюс світу. Р’ – південний полюс світу. Небесний мерідіан. Полуденна лінія. Вісь світу. ПППрямовисна лінія

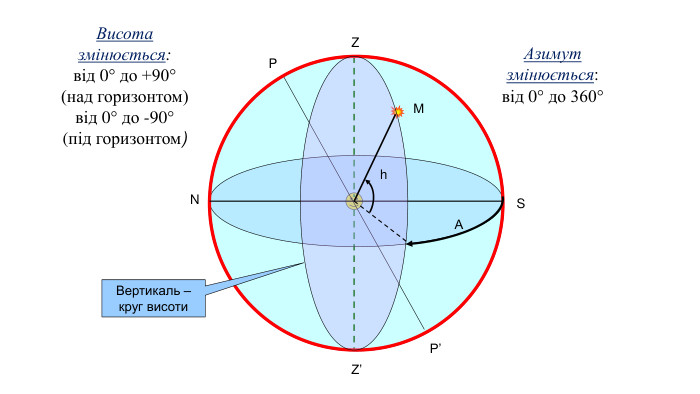
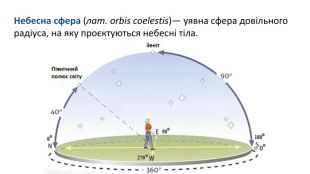
Горизонтальні координати. В горизонтальній системі координат положення об’єкта визначається відносно горизонту і відносно напрямку на південь (S). Положення зорі М задається її висотою h (кутовою відстанню від горизонта вздовж великого кола – вертикалі) і азимутом А (виміряна від заходу кутова відстань від точки півдня до вертикалі).

ZZ’NSPP’Мh. Вертикаль – круг висоти. АВисота змінюється:від 0° до +90° (над горизонтом) від 0° до -90° (під горизонтом) Азимут змінюється:від 0° до 360°

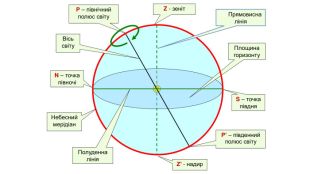
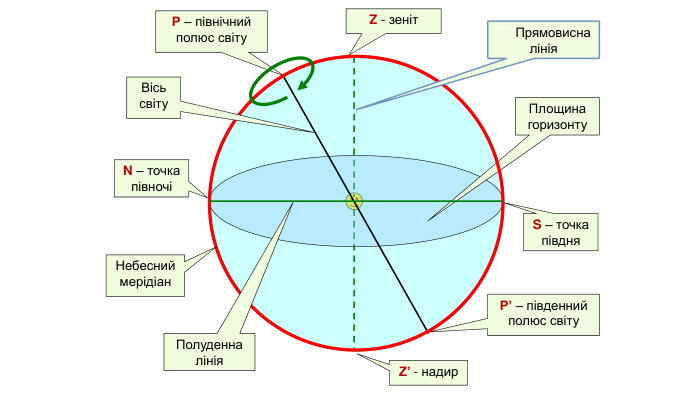
Кульмінація – проходження світила через небесний меридіан. Рухаючись навколо вісі світу, світило описує суточні паралелі. Протягом суток відбуваються дві кульмінації: верхня і нижня. У незахідного світила обидві кульмінації над горизонтом. У несхідного світила обидві кульмінації під горизонтом. Кульмінація небесних тіл

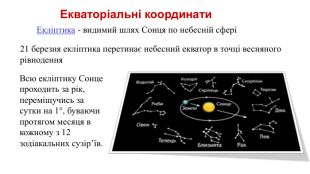
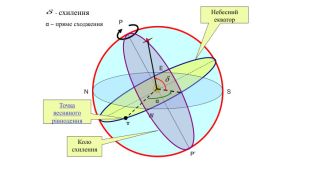
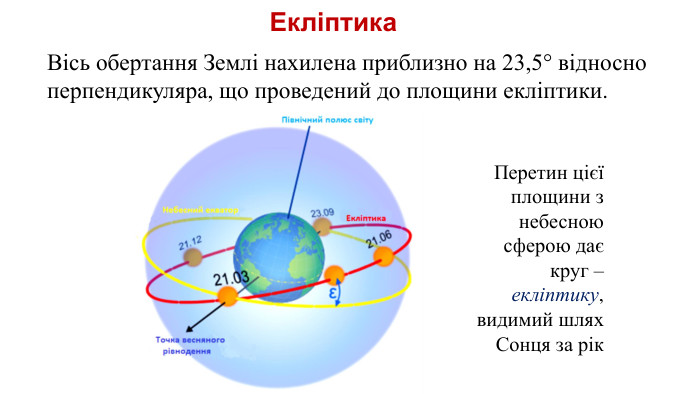
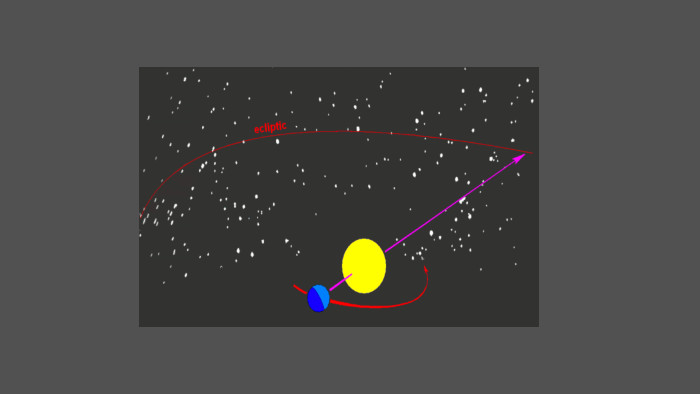
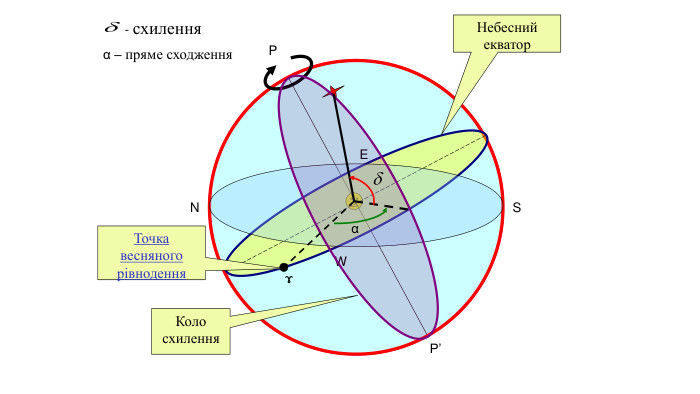
Через обертання Землі зірки постійно переміщуються відносно горизонту та сторін світу, тому координати в горизонтальній системі змінюються. Але для деяких завдань астрономії система координат має бути незалежною від положення спостерігача та часу доби. Таку систему називають «екваторіальною».8 Екваторіальні координати

Перетин цієї площини з небесною сферою дає круг – екліптику, видимий шлях Сонця за рік Вісь обертання Землі нахилена приблизно на 23,5° відносно перпендикуляра, що проведений до площини екліптики. Екліптика

Екліптика - видимий шлях Сонця по небесній сфері21 березня екліптика перетинає небесний екватор в точці весняного рівнодення. Всю екліптику Сонце проходить за рік, переміщучись за сутки на 1°, буваючи протягом месяця в кожному з 12 зодіакальних сузір’їв. Екваторіальні координати

PP’Небесний екватор. WENSКоло схиленняɤТочка весняного рівнодення - схиленняαα – пряме сходження

«Пряме сходження» вимірюється від точки весняного рівнодення до круга схилення зорі.«Схилення» зорі вимірюється її кутовою відстанню до півночі або півдня від небесного екватора. . Екваторіальні координати «Пряме сходження» змінюється від 0° до 360° або від 0 до 24 годин. Увага!

Практикум розв’язування задач

1. Зоря спостерігається у верхній кульмінації в бік північного полюса світу від точки зеніту (див. рисунок). Доведіть, що в цьому випадку географічна широта місця 𝜑=𝛿−90°+h, де δ і h – схилення і висота зорі.  ZZ’NSP’PQQ’МϕδОh. Розглянемо УВАЖНО рисунок∠МО𝑁 Схилення зорі h визначається кутом∠МО𝑁=∠РО𝑁+∠РОМ=𝜑+∠РОМ В свою чергу. Далі необхідно знайти кут ∠РОМ − ? ∠РОМ=90°−∠𝑄ОМ=90°−𝛿 (так як вісь світу перпендикулярна до небесного екватора, тобто PP’Ʇ QQ’)Отже, ∠МО𝑁 = 𝜑+90°−𝛿   h = 𝜑+90°−𝛿  𝜑=𝛿−90°+h 

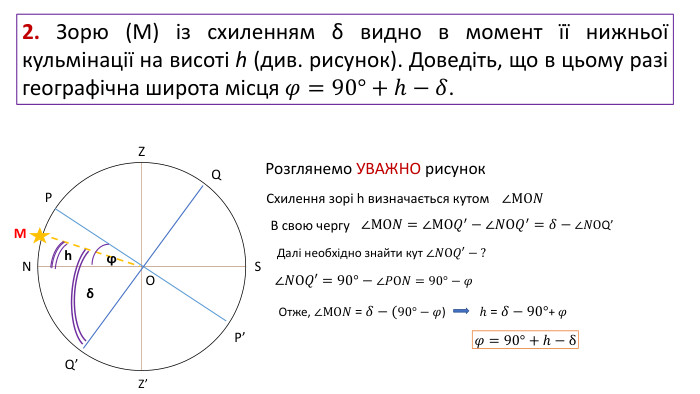
2. Зорю (М) із схиленням δ видно в момент її нижньої кульмінації на висоті h (див. рисунок). Доведіть, що в цьому разі географічна широта місця 𝜑=90°+h−𝛿.  ZZ’NSP’PQQ’МϕδОh. Розглянемо УВАЖНО рисунок∠МО𝑁 Схилення зорі h визначається кутом∠МО𝑁=∠МО𝑄′−∠𝑁О𝑄′=𝛿−∠𝑁ОQ’ В свою чергу. Далі необхідно знайти кут ∠𝑁О𝑄′ − ? ∠𝑁О𝑄′=90°−∠𝑃О𝑁=90°−𝜑 Отже, ∠МО𝑁 = 𝛿−(90°−𝜑) h = 𝛿 − 90°+ 𝜑 𝜑=90°+h−δ 

3. Розрахувати висоту верхньої і нижньої кульмінації Ель-Нат (β Тельця) у Ірпені (широта - 50° 31’), схилення зорі +28°37’. На якій широті ця зоря не заходить. Дано:𝜑=50°31′𝛿= + 28°37′ hв - ?Відповідь: hв= 60°06’, hн= 10°52’, 𝜑н= 61°23′  hн - ?Верхня кульмінація зорі визначається за формулою Розв’язанняhв=90−𝜑+𝛿 hв=90−50°31′+28°37′ = 60°06' Нижня кульмінація зорі визначається за формулою hн=90−𝜑−𝛿 hн=90−50°31′−28°37′ = 10°52' Зоря не заходить, якщо hн = 0 для нижньої кульмінації 0=90−𝜑−𝛿 𝜑=90−𝛿 𝜑=90−28°37′= 61°23′ 𝜑н − ? 

4. Сіріус (α В. Пса) був у верхній кульмінації на висоті 10°. Чому дорівнює широта місця спостереження. Дано:h = 10°ϕ - ? Cхилення Сіріуса знаходимо з таблиці додатка (записуємо його округлення значення) δ = -17°З формули h=90−𝜑+𝛿 𝜑=90−h+𝛿 Відповідь: 𝜑=63°  Розв’язання𝜑=90−10°−17°=63° Обчислюємо

5. У місті Дніпро (ϕ=48°30’) зоря Мегрец, що не заходить, у момент верхньої кульмінації спостерігається на зенітній відстані z= 8°49’, а місті Ризі (ϕ=56°58’) зорю Мірам у нижній кульмінації видно на висоті h=22°39’. Визначте схилення кожної з цих зір. Розв’язання. Дано:ϕ=48°30’z= 8°49’ І. Розглянемо спочатку зорю Мегрец δ - ?h = 90° - zh = 90° - 8°49’ = 81°11'𝜑=𝛿−90°+h З формули визначення географічної широти (див. Задача 1)Визначаєм схилення𝛿=90°+φ−h 𝛿=90°+48°30’−81°11′=138°30′−81°11′ 𝛿=57°19' style.colorfillcolorfill.typefill.on

5. (продовження) У місті Дніпро (ϕ=48°30’) зоря Мегрец, що не заходить, у момент верхньої кульмінації спостерігається на зенітній відстані z= 8°49’, а місті Ризі (ϕ=56°58’) зорю Мірам у нижній кульмінації видно на висоті h=22°39’. Визначте схилення кожної з цих зір. Розв’язання. Дано:ϕ=56°58’h= 22°39’ І. Розглянемо зорю Мірамδ - ?З формули визначення географічної широти для нижньої кульмінації (див. Задача 2)Визначаєм схилення𝛿=90°+h−φ 𝛿=90°+22°39’−56°58′=112°39′−56°58′=111°99′−56°58′ 𝛿=55°19' 𝜑=90°+h−δ 

6. Обчисліть висоти, на яких спостерігається Сонце в момент справжнього полудня: 23 вересня – у м. Мелітополі (ϕ=46°51’), 22 грудня – м. Острозі (ϕ=50°20’), 21 березня – м. Тюмені (ϕ=57°10’), 22 червня – в м. Тбілісі – (ϕ=41°43’). Відповідь: 43°09’; 16°13’; 32°50’; 71°44'   Дано: Мелітополь φ= 46°51'  Розв’язання. Острог ϕ=50°20’ Тюмені ϕ=57°10’ Тбілісі ϕ=41°43’h=90°−𝜑+𝛿 Мелiтополь. 23 вересня (осіннє рівнодення)δ = 0h=90°−46°51′+0=89°60′−46°51′ = 43°09' Острог. 22 грудня (зимове рівнодення)δ = -23°27'h=90°−46°51′−23°27′=89°60′−73°47′ = 16°13' Тюмень. 21 березня (весняне рівнодення)δ = 0h=90°−57°10′+0=89°60′−57°10′ = 32°50' Тбілісі. 22 червня (літнє рівнодення)δ = +23°27'h=90°−41°43′+23°27′=89°60′−18°16′ = 71°44' h - ?

7. У м. Бахчисараї (ϕ = 44°45’) Сонце спостерігалось на полуденній висоті h = 50°. Знайти схилення Сонця.ϕ = 44°45' Дано:h = 50°Відповідь: δ=4°45′ δ - ?Розв’язання. Широта місцевості, коли Сонце спостерігалося на полуденній лінії визначається формулою𝜑=90°+δ−h Звідси слідує δ=𝜑+h−90° δ= 44°45′+50°−90°=94°45′−90° = 4°45' 

8. Під яким кутом небесний екватор перетинає горизонт (в точках сходу і заходу) для спостерігача, що знаходиться на широті 40°? Які це кути, якщо географічна ширoтa місця спостереження буде 10; 20; 50; 70; -40°? Кут перетину небесного екватора з площиною горизонту: ∠𝑄𝑂𝑆= ∠𝑄𝑂𝑃′−∠𝑆𝑂𝑃′=90°−φ  Для 40° 90°−40° = 50°  Для 10° 90°−10° = 80°  Для 20° 90°−20° = 70°  Для 50° 90°−50° = 40°  Для 70° 90°−70° = 20°  Для -40° (∠𝑁𝑂𝑄′)  90°−40° = 50° (нижче горизонту) Відповідь: 50°; 80°; 70°; 40°; 20°; 50°.

9. В який час і на якій висоті кульмінує Марс, що знаходиться в протистоянні в Києві (50°27'). В якому зусір’ї це відбувається? ϕ = 50°27' Дано:δ = 23,5°h - ?Розв’язання22 грудня Сонце знаходиться в точці зимового сонцестояння. Оскільки Марс в протистоянні, то він в той час знаходиться біля точки літнього сонцестояння ( в сузір’ї Близнят). Верхня кульмінація цієї точки 22 грудня має схилення цієї точки δ = 23,5° Отже, Марс буде кульмінувати на висоті h=90°−𝜑+𝛿 h=90°−50°27'+23,5°=63°23' Відповідь: 63°23’  

10. Широта м. Чернігів (φ=51°29'). Чи можна спостерігати яскраву зорю Фомальгаут (δ=-29°30') ? ϕ = 51°29' Дано:δ = -29°30'h - ?Розв’язанняh=90°−𝜑+𝛿 h=90°−51°29'−29°30'=89°60'−51°29′−29°30′≈9° Можна спостерігати, але досить низько над горизонтом. Відповідь: Можна. h=9°.  

Література. Пришляк М. П. Астрономія 11 клас (рівень стандарту).-Харків, Вид-во «Ранок», 2019 Чепрасов В. Г. Завдання, запитання і задачі з астрономії. – Київ, Вид-во «Радянська школа», 1984 Малахов Г.І., Страут Е. К. Дидактичний матеріал з астрономії. – Вид-во «Просвіта», 1979 Дагеєв М. М. Збірник задач з астрономії. Вид-во «Просвіта», 1980 Воронцов-Вельямінов Б. Астрономія. Підручник для 10 класу середньої школи. Видання 5-е. М.: Учпедгиз 1976р. https://www.youtube.com/watch?v=JNrnv3p. VPts – Астрономія. Урок розв’язування астрофізичних задач в 11 класі ЛФМЛ

Кінець