Заняття №26 на тему «Точка перетину бісектрис трикутника. Центр кола, вписаного в трикутник. Центр зовні вписаного кола»

Заняття №26 на тему «Точка перетину бісектрис трикутника. Центр кола, вписаного в трикутник. Центр зовні вписаного кола»

Дане заняття відповідає діючій програмі факультативного курсу з математики для 7 класу Бевз В. Г, Бурда М. І., Прокопенко Н. С. «За лаштунками шкільної математики». Воно містить теоретичний матеріал, що відображає тему, приклади завдань з розв'язками та вправи для самостійного виконання.

Враховуючи інтереси та нахили учнів, їхню підготовленість, вчитель може доповнювати зміст заняття додатковим матеріалом, змінювати та удосконалювати методику проведення.

Тема 3. Особливі точки та лінії в трикутнику.

Геометричні побудови

Заняття 26

Точка перетину бісектрис трикутника. Центр кола, вписаного в трикутник. Центр зовні вписаного кола

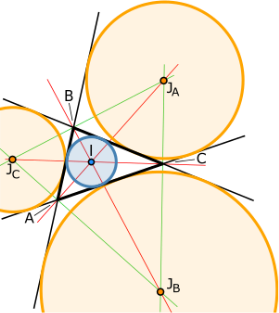Вписане коло трикутника — це найбільше коло, розташоване в трикутнику, яке дотичне до трьох його сторін. Центр вписаного в трикутник кола називають інцентром. Інцентром також називають точку перетину бісектрис трикутника. Традиційно позначають латинською літерою .

 Зовнішнє вписане коло (також зовнівписане) трикутника — це коло, яке лежить за межами трикутника дотичне до одної з сторін трикутника і також дотичне до продовження інших двох сторін. Кожен трикутник має три зовнішні вписані кола, кожне з яких дотичне до одної з сторін трикутника. Центр зовнішньо вписаного кола традиційно позначають латинською літерою з індексом - назвою відповідної вершини трикутника, наприклад, .

Центр вписаного кола можна знайти, як точку перетину трьох бісектрис внутрішніх кутів. Формули для обчислення довжини бісектриси трикутника (, формула Лагранжа )

Центр зовнівписаного кола можна знайти, як точку перетину бісектриси внутрішнього кута і двох бісектрис зовнішніх кутів. З цього випливає, що центр вписаного кола разом з трьома центрами зовнішніх вписаних кіл утворюють ортоцентричну систему.

Властивості:

1. Інцентр лежить на однаковій відстані від усіх сторін трикутника.
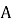
2. Інцентр ділить бісектрису кута у відношенні , де , , - сторони трикутника.
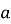
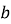
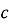
3. Теорема про трилисник (або лема про тризубець). Якщо продовження бісектриси кута перетинає описане навколо трикутника коло в точці , то справедлива рівність: , де - центр зовнішього вписаного кола, що дотикається до сторони .
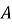
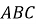
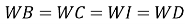
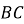
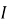
4. Формула Ейлера. Квадрат відстані між інцентром 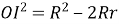і центром описаного кола дорівнює , де і - радіуси відповідно описаного та вписаного кіл.

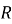
Розв’язування задач та вправ

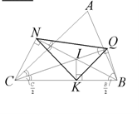
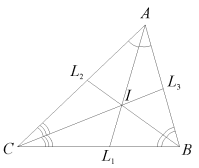
•             Продовження бісектрис внутрішніх кутів трикутника 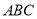перетинають описане навколо нього коло в точках 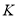, , 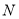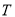(рис.7). – центр описаного кола. – інцентр трикутника (точка перетину його бісектрис). Довести, що .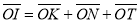

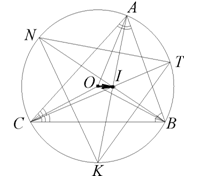Розв’язання. Неважко показати, що інцентр трикутника є ортоцентром у трикутнику (доведіть цей факт!). До того ж, точка залишається центром описаного кола і для трикутника .

Тоді за формулою Гамільтона: .

• Нехай точки ; ; – основи висот трикутника 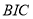. Доведіть, що

а) трикутники і подібні;

б) інцентри цих трикутників співпадають!

Розв’язання. Навколо чотирикутника можна описати коло з діаметром , оскільки . Звідси (вписані, спираються на одну дугу).

Аналогічно можна показати, що і також .

Таким чином, трикутники і подібні – за двома кутами.

Оскільки та є бісектрисами кутів і , то – також інцентр для .

Завдання для самостійного розв’язування.

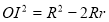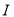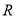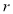1. Довести формулу Ейлера: ( – інцентр, і – радіуси описаного і вписаного кіл).
2. Прямокутник вписано в коло, – довільна точка меншої дуги 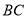. Точки 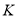; ; 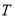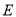– основи перпендикулярів, проведених із точки 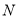на 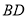, , 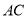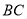відповідно. Доведіть, що точка 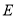є точкою перетину бісектрис (інцентром) у трикутнику .
3. Доведіть властивість інцентра (точки перетину бісектрис):

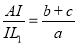
 Використана література

1. Адлер А. Теорія геометричних побудов, Переклад з німецької Г. М. Фіхтенгольца. Видання третє. Л., Навчпедвид, 1940—232 с.
2. Бевз Г. П. Геометрія трикутника. — Київ: Генеза, 2005. — 120 с. ISBN 966-504-431-1
3. Бевз Г. П., Бевз В. Г., Владімірова Н. Г. Геометрія: Підручник для 7-9 кл. — Київ: Вежа, 2004. — 309 с. ISBN 966-7091-66-Х
4. Воронець О. М. Геометрія циркуля, Популярна бібліотека з математики під загальною редакцією Л. О. Люстерника, М.- Л., ОНТІ, 1934 — 40 с.
5. Кушнір І. А. Трикутник і тетраедр в задачах: кн. для вчителя / І. А. Кушнір. — К. : Радянська школа, 1991. — 208 с.
6. Манін Ю. І., Про розв'язність задач на побудову за допомогою циркуля та лінійки, Енциклопедія елементарної математики книга четверта (геометрія), М., Фізматвид, 1963. — 568с.
7. Петерсен Ю. Методи і теорії розв'язку геометричних задач на побудову, Москва, типографія Э.Ліснера та Ю.Романа, 1892 — VIII + 114с.
8. Прасолов В. В.. Три класичні задачі на побудову. Подвоєння куба, трисекція кута, квадратура кола. М.: Наука, 1992. 80 с. Серія <Популярні лекції з математики>, випуск 62.
9. Щетников А. І. Як було знайдено де-які розв'язки трьох класичних задач древності? Математична освіта, № 4 (48), 2008, с. 3-15.
10. Слива Н. В.Математика 7клас. Факультативний курс http://www.fak-matematika_7_klas_sliva_n.v.