Заняття № 34 «Круги Ейлера»

Заняття № 34 «Круги Ейлера»

Дане заняття відповідає діючій програмі факультативного курсу з математики для 7 класу Бевз В. Г, Бурда М. І., Прокопенко Н. С. «За лаштунками шкільної математики». Воно містить теоретичний матеріал, що відображає тему, приклади завдань з розв'язками та вправи для самостійного виконання.

Враховуючи інтереси та нахили учнів, їхню підготовленість, вчитель може доповнювати зміст заняття додатковим матеріалом, змінювати та удосконалювати методику проведення.

Тема 4. Математична мозаїка

Заняття 34

Круги Ейлера

Петербургський математик Леонард Ейлер є одним з видатних математиків 18ст. Він вніс великий вклад в розвиток як елементарної, так і вищої математики. За своє життя (1707-1783) він написав більш як 850 наукових робіт. В одній з них і з’явилися круги, які назвали кругами Ейлера.

Він писав, що вони «дуже підходять для того, щоб полегшити наші роздуми». Поряд з кругами в задачах застосовують прямокутники  та інші фігури.

Деякі задачі математики розв’язуються за допомогою кругів Ейлера. З допомогою них зручно відображати відношення між множинами.

Розв'язування задач і вправ.

•             В класі 35 учнів. З них 20 займаються в математичному гуртку, 11 – в біологічному, 10 учнів не  відвідують ці гуртки. Скільки біологів захоплюються математикою? 

Розв'язання.

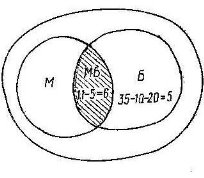Зобразимо ці круги на малюнку. М- математики, Б – біологи, МБ – математики-біологи.

Як бачимо, 6 біологів захоплюються математикою.

•             В піонерському таборі 70 дітей. З них 27 займаються в драмгуртку, 32 – співають в хорі, 22 – займаються спортом. В драмгуртку 10 дітей з хору, в хорі – 6 спортсменів, в драмгуртку - 8 спортсменів, 3 спортсмени відвідують драмгурток і хор. Скільки дітей не співають в хорі, не займаються спортом і не займаються в драмгуртку? Скільки дітей займаються лише спортом?

Розв'язання.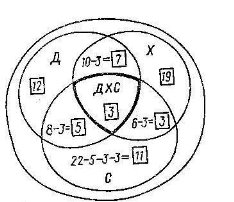

Зобразимо на малюнку круги Ейлера.  Д – драмгурток, Х – хор, С – спортсмени. 10 дітей не співають в хорі, не займаються спортом і не займаються в драмгуртку, 11 дітей  займаються тільки спортом.

Завдання для самостійного розв'язування.

1. В класі 38 чоловік. З них 16 грають в баскетбол, 17 – в хокей, 18 – в волейбол. Захоплюються двома видами спорту – баскетболом і  хокеєм – четверо, баскетболом і  волейболом – троє, волейболом і хокеєм – п’ятеро. Троє не захоплюються ні баскетболом, ні хокеєм, ні волейболом. Скільки дітей захоплюються одночасно трьома видами спорту? Скільки дітей захоплюються лише одним з цих видів спорту?
2. В класі навчаються 40 учнів. З них: з  українській мові мають трійки 19 учнів, з математики – 17 учнів, з фізики – 22 учні. Тільки з одного предмета мають трійки: з мови - 4 учні, з математики – 4 учні, з фізики – 11 учнів. Сім учнів мають трійки і з математики, і з фізики, з них  п’ятеро мають трійки і  з мови. Скільки учнів вчаться без трійок? Скільки учнів мають трійки  по двох із трьох предметів?
3. Зі 100 іноземних туристів 75 знали німецьку  мову, 83- французьку. Скільки туристів знали і французьку, і німецьку мову одночасно?

Практичні завдання.

1. Виготовити листок Мебіуса.
2. Пофарбувати поверхню, не відриваючи олівця.
3. Розрізати листок Мебіуса по середній лінії.

Використана література

1. Адлер А. Теорія геометричних побудов, Переклад з німецької Г. М. Фіхтенгольца. Видання третє. Л., Навчпедвид, 1940—232 с.
2. Бевз Г. П. Геометрія трикутника. — Київ: Генеза, 2005. — 120 с. ISBN 966-504-431-1
3. Бевз Г. П., Бевз В. Г., Владімірова Н. Г. Геометрія: Підручник для 7-9 кл. — Київ: Вежа, 2004. — 309 с. ISBN 966-7091-66-Х
4. Воронець О. М. Геометрія циркуля, Популярна бібліотека з математики під загальною редакцією Л. О. Люстерника, М.- Л., ОНТІ, 1934 — 40 с.
5. Кушнір І. А. Трикутник і тетраедр в задачах: кн. для вчителя / І. А. Кушнір. — К. : Радянська школа, 1991. — 208 с.
6. Манін Ю. І., Про розв'язність задач на побудову за допомогою циркуля та лінійки, Енциклопедія елементарної математики книга четверта (геометрія), М., Фізматвид, 1963. — 568с.
7. Петерсен Ю. Методи і теорії розв'язку геометричних задач на побудову, Москва, типографія Э.Ліснера та Ю.Романа, 1892 — VIII + 114с.
8. Прасолов В. В.. Три класичні задачі на побудову. Подвоєння куба, трисекція кута, квадратура кола. М.: Наука, 1992. 80 с. Серія <Популярні лекції з математики>, випуск 62.
9. Щетников А. І. Як було знайдено де-які розв'язки трьох класичних задач древності? Математична освіта, № 4 (48), 2008, с. 3-15.
10. Слива Н. В.Математика 7клас. Факультативний курс http://www.fak-matematika_7_klas_sliva_n.v.