Презентація "Прикладне застосування функцій"

Прикладне застосування функцій

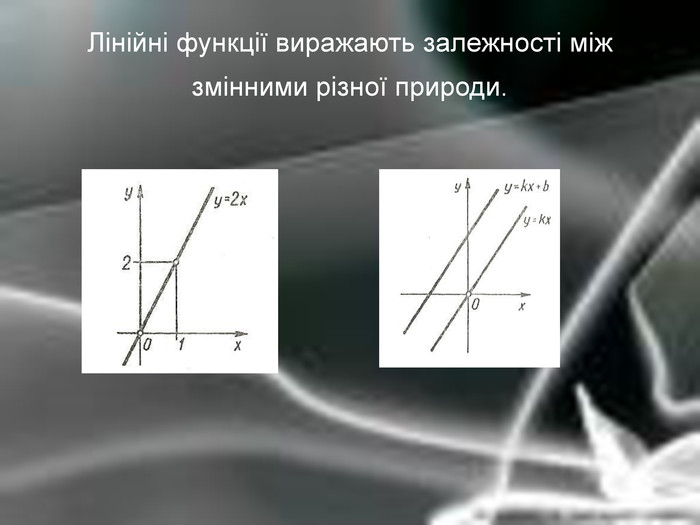
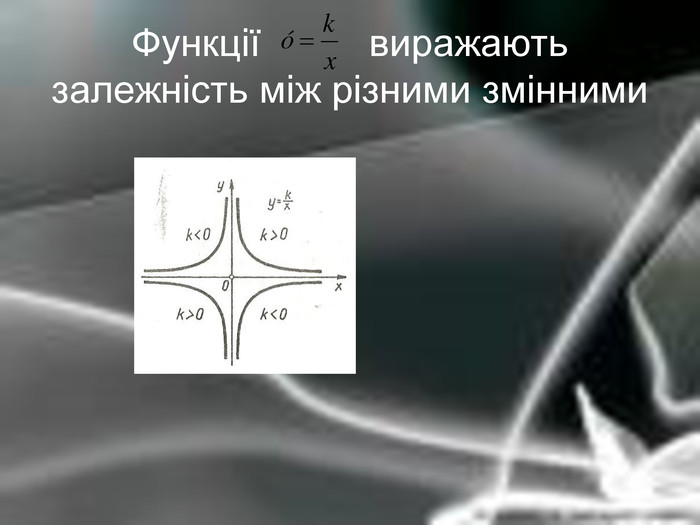
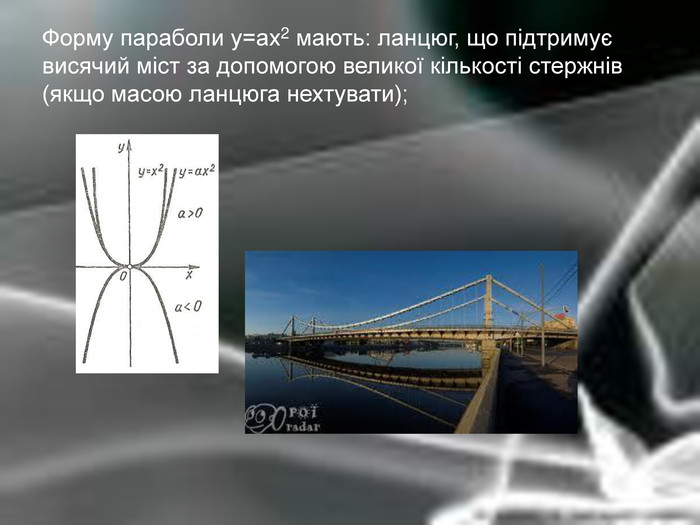
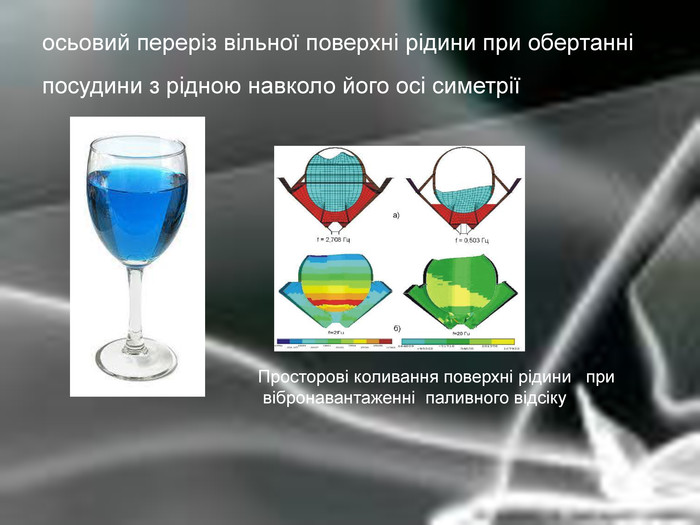
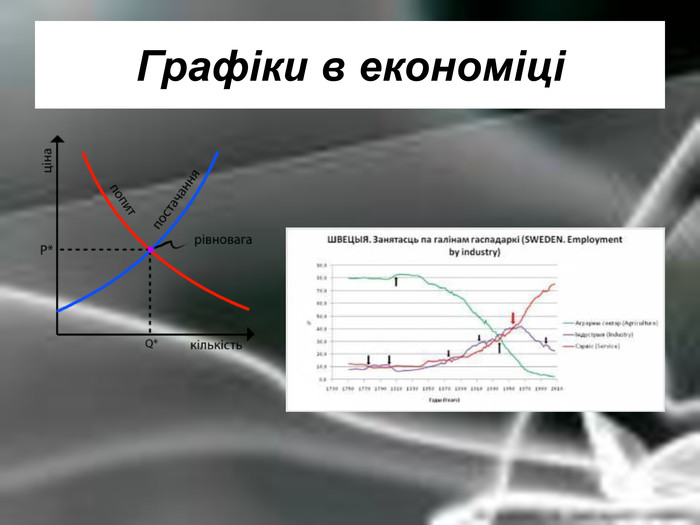
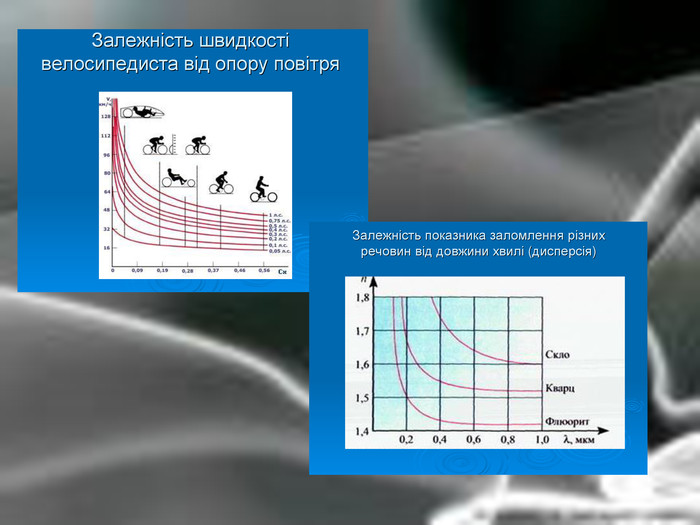
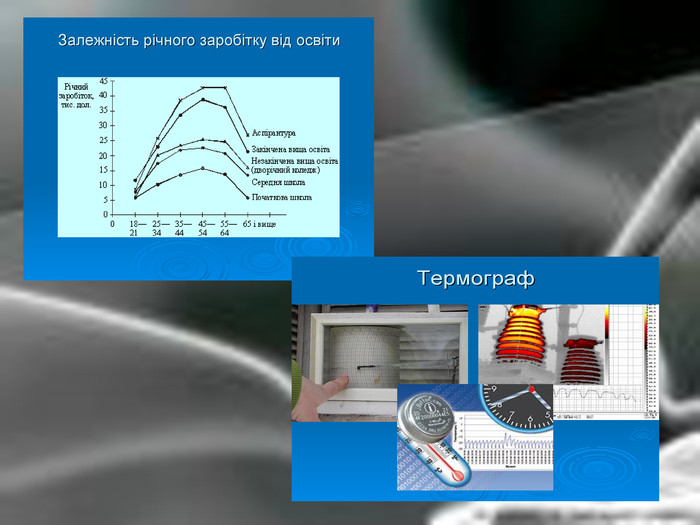
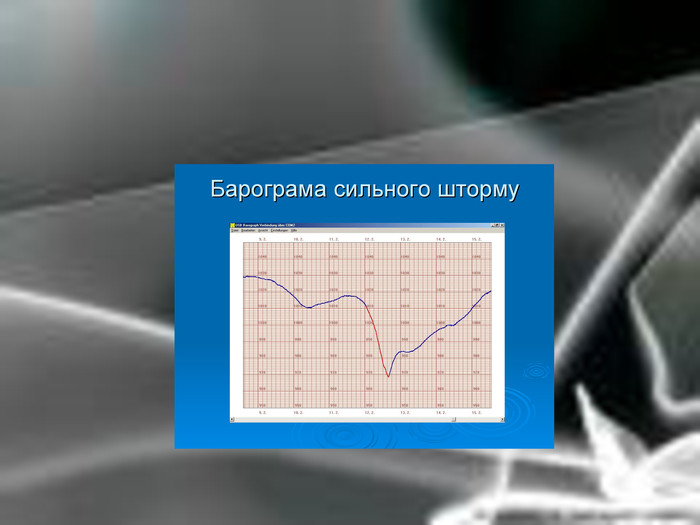
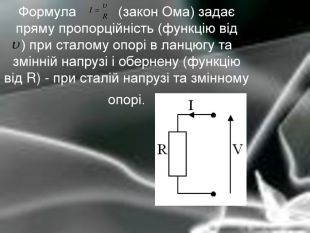
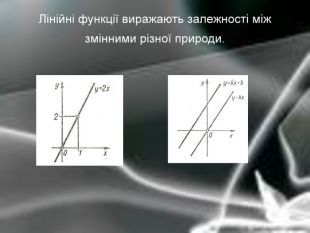
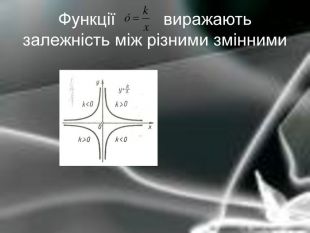
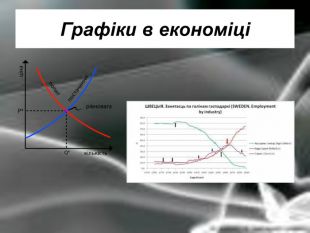
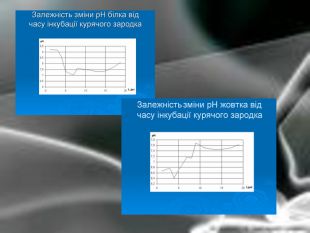
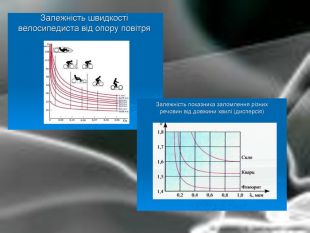
Матеріальна єдність світу виявляється у взаємозв’язку і взаємообумовленості різних явищ і процесів, що відбуваються у природі. Розглядаючи їх, доводиться враховувати залежності одних величин від інших. Наприклад, залежність довжини шляху від часу, залежність кількості купленого товару на певну суму від ціни, залежність між площею круга і його радіусом. Необхідність вивчення на практиці залежностей між змінними різної природи привела до поняття функції в математиці.

ПРИКЛАДИ

Залежність довжини шляху S , пройденого тілом, яке рухається рівномірно, від часу t є функцією, що задається формулою , де S0 початковий шлях, який пройшло тіло; v – швидкість, яка є сталою при рівномірному русі.

Якщо учні класу, що складається з 25 осіб, чергують протягом січня, крім тих днів, які припадають на неділю, то кожному з днів січня відповідає певний черговий. Незалежною змінною тут є дні січня, залежною-черговий. Маємо функцію, областю визначення якої є множинна днів січня (без тих, що придають на неділю), а областю зміни - множина учнів класу.

Активна електрична енергія, яка витрачається в колі змінного струму за час t , є функцією часу і при сталій потужності Р виражається формулою

За допомогою графіка функції можна фіксувати протягом кількох років висоту дерева, яке росте.

Формула (закон Ома) задає пряму пропорційність (функцію від ) при сталому опорі в ланцюгу та змінній напрузі і обернену (функцію від R) - при сталій напрузі та змінному опорі.

Лінійні функції виражають залежності між змінними різної природи.

Наприклад: а) залежність довжини шляху s, який пройде тіло при рівному русі, від часу t визначають за формулою де s0 - початковий шлях, - стала швидкість

б) залежність довжини металевого стержня від температури при нагріванні задають формулою де - довжина стрижня при t=0, k – коефіцієнт лінійного розтягу

в) вартість N телеграми обчислюється за формулою N=5x+20, де х – кількість слів, 5 коп. – вартість одного слова, 20 коп. – попередня оплата

г) вартість проїзду в таксі можна обчислити за формулою Р=20п+20, де п - кількість кілометрів (відстань), що проїхав пасажир, 20 коп. – вартість проїзду одного кілометра, 20 коп. – сума, яка автоматично фіксується на лічильнику, коли пасажир сідає в таксі

Функції виражають залежність між різними змінними

а) залежність кількості купленого товару на задану суму грошей від ціни товару;

б) залежність сили струму від опору провідника при сталій напрузі (закон Ома);

в) залежність між тиском газу і об’ємом, який він заповнює, (закон Бойля - Маріотта), де k – стала;

г) залежність часу від швидкості руху , де s – довжина шляху

За допомогою функції у=х2 виражають залежність площі квадрата від довжини його сторони.

На практиці, у фізиці, техніці частіше застосовують функцію у=ах2, де а – число. За допомогою цієї функції виражають, наприклад: а) залежність площі круга від радіуса S=πr2

б) залежність кінетичної енергії тіла від його швидкості W= ;

в) залежність довжини шляху вільно падаючого тіло від часу (якщо опором середовища нехтувати)

Форму параболи у=ах2 мають: ланцюг, що підтримує висячий міст за допомогою великої кількості стержнів (якщо масою ланцюга нехтувати);

траєкторія снаряда, що летить

осьовий переріз автомобільної фари

Просторові коливання поверхні рідини при вібронавантаженні паливного відсіку осьовий переріз вільної поверхні рідини при обертанні посудини з рідною навколо його осі симетрії

Функція у=x3. Ця функція витрачає, наприклад, залежність об’єму куба від довжини його ребра.

Графік у=ах3 використовують проектувальники залізниць та автомобільних шляхів для здійснення плавного переходу від прямо лінійних ділянок шляху до криволінійних.

Зокрема, за допомогою цієї функції вражають залежність періоду Т малих коливань математичного маятника від його довжини l: Т=2 , де g – прискорення вільного падіння. На практиці використовують функцію .

ЗАДАЧІ

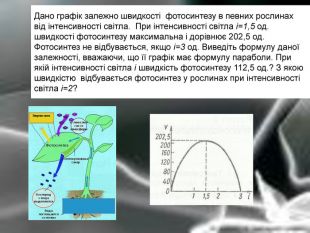
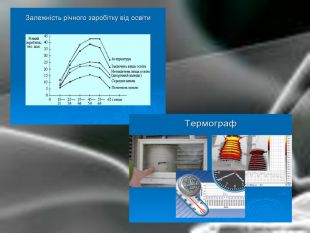
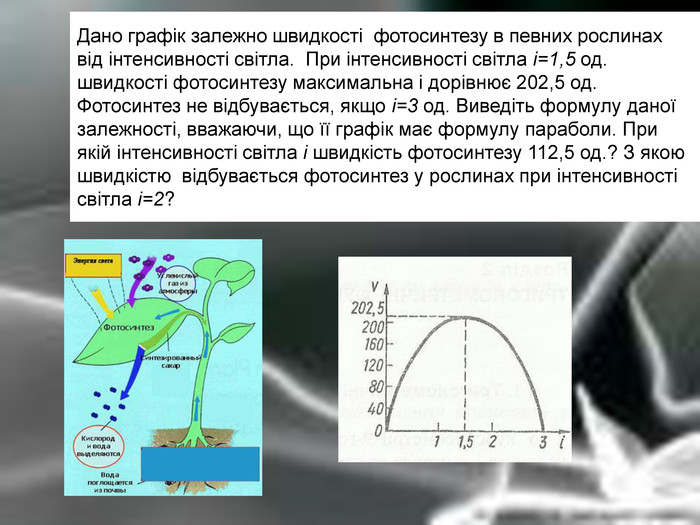
Дано графік залежно швидкості фотосинтезу в певних рослинах від інтенсивності світла. При інтенсивності світла і=1,5 од. швидкості фотосинтезу максимальна і дорівнює 202,5 од. Фотосинтез не відбувається, якщо і=3 од. Виведіть формулу даної залежності, вважаючи, що її графік має формулу параболи. При якій інтенсивності світла і швидкість фотосинтезу 112,5 од.? З якою швидкістю відбувається фотосинтез у рослинах при інтенсивності світла і=2?

Використовуючи дані таблиці, побудуйте графік залежності витрати палива в літрах на 100 км шляху автомобілем «Москвич-2141» від його швидкості.

Опір сухої горизонтальної дороги з твердим покриттям руху автомобіля, швидкість якого , виражає формулою Дослідити, як змінюється опір дороги при різній швидкості автомобіля, м/с. При якій швидкості опір буде найменшим?

На рисунку показано графік переміщення тіла, яке рухається рівноприскорено. Яку швидкість воно буде мати через 3 с, якщо початкова швидкість ?

Де в житті вам доводилося зустрічатися з графіками? • На уроках математики; • У довідковій літературі; • Графік руху потягів; • Графік зміни температур

Прилад, що демонструє принцип роботи сейсмографа. Сейсмограф Використовуючи свідчення сейсмографів (приладів тих, що безперервно фіксують коливання ґрунту і що будують спеціальні графіки - сейсмограми) геологи можуть передбачити наближення землетрусу або цунамі.

Сучасний сейсмограф Kinemetrics Сейсмограма

    "Дракон, що грається з жабами" або перший в світі сейсмограф

Кардіограф

Приклади кардіограм

Графіки в економіці