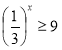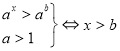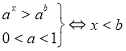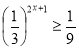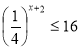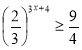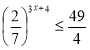Заняття "Показникові рівняння та нерівності"
ПЛАН ЗАНЯТТЯ
Дисципліна : Математика
Дата : 29.10.15
Група : ЕО-15
Кількість студентів за списком: 25
Спеціальність: 5.05030103 “Експлуатація та ремонт гірничого електромеханічного обладнання та автоматичних пристроїв”
Місце проведення: кабінет вищої математики, № 28
Тема заняття : Показникові рівняння та нерівності. Розв’язування вправ. Самостійна робота
Мета заняття:
Методична – удосконалити методику впровадження інтегральної технології у викладання математики;
Дидактична – узагальнити та систематизувати знання про показникову функцію, її властивості, формувати уміння та навички застосування цих знань при розв’язанні вправ з теми, перевірити отримані знання та уміння при виконанні самостійної роботи;
Розвиваюча – сприяти виробленню навичок розв'язання показникових рівнянь і нерівностей, розвивати пам’ять, навички самостійної роботи;
Виховна – виховувати почуття відповідальності, організованості, силу волі,
наполегливість у досягненні мети, формувати вміння працювати
в команді.
Вид заняття : практичне заняття
Тип заняття : узагальнення та систематизації знань та умінь з контролем знань
Методичне забезпечення:
- Технологічна карта заняття;
- Таблиця «Показникові рівняння та нерівності»;
- Картки контролю теоретичних знань та для виконання самостійної
роботи;
- Презентація заняття.
Технічні засоби навчання:
- Мультимедійний проектор
- Персональний комп’ютер
Міжпредметні зв’язки:
Забезпечуючі: «Українська мова», «Фізика»
Забезпечуємі: «Інформатика та комп’ютерна техніка», «Загальна електротехніка», «Опір матеріалів», «Гідравліка»
Література
Основна:
1. Афанасьєва О.М., Бродський Я.С., Павлов О.Л., Сліпенько А.К. Математика. Підручник. К., Вища школа, 2001
2. Афанасьєва О.М., Бродський Я.С., Павлов О.Л., Сліпенко А.К. Дидактичні матеріали з математики. К., Вища школа, 2001
3. Нелін Є.П. Алгебра та початки аналізу: підручник для 10 класу загальн.учбових закладів. Х.: Гімназія, 2010
Додаткова :
1. Богомолов II.В. Практические занятия по математике. М.: Высш. шк., 1979, 1983, 1990
2. Савенко Т.П., Паньков В.Г., Попов Ю.Н. Задачи по алгебре и началам анализа. Часть І / Под ред. И.М. Конета. – Каменец – Подольский: Абетка-НОВА, 2004
3. Збірник заданий для державної підсумкової атестації з математики. 11 класс. Ред. З.І. Слєпкань. – Харьків, “Гімназія”, 2014
Хід заняття
1. Організаційний момент. 1 хв.
Привітання зі студентами
Відмітка у журналі відсутніх
Перевірка готовності до заняття студентів, аудиторії
2. Ознайомлення студентів з темою та навчальними цілями заняття 2 хв.
- Тема: Показникові рівняння та нерівності. Розв’язування вправ. Самостійна робота
На цьому занятті ми систематизуємо та узагальнимо знання про показникову функцію, її властивості, показникові рівняння та нерівності, способи їх розв’язання, будемо вчитися застосовувати ці знання при виконанні вправ з теми та перевіремо рівень їх засвоєння при виконанні самостійної роботи.
Заняття проведемо у формі гри «Математичний марафон».
Чи знаєте ви, що таке марафон? Це дисципліна легкої атлетики, яка представляє собою забіг на певну дистанцію (близько 42 км). Щоб подолати таку відстань, спортсмену необхідні хороші фізичні дані. Сьогодні ми теж проведемо марафон, але математичний . Щоб його подолати, вам знадобиться сила волі, наполегливість у досягненні мети і, звичайно, ваші знання. У марафоні беруть участь дві команди (1 ряд – це команда). Ви обрали собі командира? В його обов’язки входить зробити так, щоб всі члени команди прийшли до фінішу
3. Актуалізація опорних знань. Мотивація навчання. 20 хв.
Мета. Повторити основні теоретичні знання з теми та вчитися застосовувати їх при виконанні стандартних вправ.
Викладач. Якщо подивитися де застосовується тема «Показникова функція», то ми будемо дуже здивовані, тому що багато процесів в науці та повсякденному житті описується показниковою функцією.
Ось деякі з Нобелівських лауреатів, які отримали премію за дослідження в області фізики з використанням показовою функції:
П'єр Кюрі - 1903 р., Річардсон Оуен - 1928 р., Ігор Тамм - 1958 р., Луїс Альварес - 1968 р., Альфвен Ханнес - 1970 р., Роберт Вільсон Вудро - 1978 р.
Показникова функція 
описує зростання кількості бактерій, де N – число колоній бактерій в момент часу t, а t – час розмноження. І таких прикладів можна навести багато з різних галузей науки.
Ви, напевно, помічали, що якщо зняти киплячий чайник з вогню, то спочатку він швидко остигає, а потім охолодження йде набагато повільніше. Справа в тому, що швидкість охолодження пропорційна різниці між температурою чайника і температурою навколишнього середовища. Чим менше стає ця різниця, тим повільніше остигає чайник. Якщо спочатку температура чайника дорівнювала Т0, а температура повітря T1, то через t секунд температура Т чайника виразиться формулою:
T=(T1-T0)e-kt+T1,
де k - число, що залежить від форми чайника, матеріалу, з якого він зроблений, і кількості води, яка в ньому знаходиться.
Ось чому необхідно дуже добре знати, що таке показникова функція і як її можна застосовувати
Починаємо наш марафон.
Завдання.
- Фронтальне опитування. Завдання виконуємо усно. 15 хв.
|
№ з/п |
І команда |
ІІ команда |
|
1 |
Яка функція називається показниковою?
(Функція вигляду
|
З наведених функцій виберіть показникову функцію:
1)
4) (Відповідь:2), 3)) |
|
2 |
Перерахуйте основні властивості показникової функції (Область визначення – множина дійсних чисел. |
Знайдіть область визначення функції: 1)
2) (Відповідь:1) D(y) = R, 2) D(y) =[0; + )) |
|
|
Множина значень – додатні значення, тобто Е(у) = (0; + ) |
Які з наведених функцій є зростаючими, а які спадні?
1)
4) (Відповідь: зростаючі 1), 5), спадні – усі інші) |
|
|
При а>1функція зростаюча, а при 0<а<1 функція спадає) |
|
|
3 |
Які рівняння називаються показниковими? (Рівняння, в якому невідома знаходиться в показнику степені називається показниковим рівнянням) |
Виберіть з наведених показникові рівняння: 1)
5) (Відповідь:2), 3), 5), 6) |
|
4 |
Які рівняння, з наведених в пункті 3 є найпростішими показниковими рівняннями (Відповідь:2), 3), 6) |
Які показникові рівняння називаються найпростішими?
(Рівняння вигляду |
|
5 |
Розв’яжіть нерівність:
1) (Відповідь:1) х(-; 3]; 2) х(-; 2];3) ) |
Найпростіша показникова нерівність має вигляд?
(Нерівність вигляду |
|
6 |
На яких твердженнях ґрунтується розв’язок показникових рівнянь?
|
2) Заповнення картки контролю теоретичних знань 5 хв.
Завдання. Кожен студент працює з карткою контролю теоретичних знань (Додаток А), заповнюючи пусті місця або підкреслюючи необхідні данні.
За виконання усіх завдань картки контролю студент отримає 2 бали, які додаються до кількості балів, отриманих при виконанні самостійної роботи.
Після заповнення картки студенти знайомляться з правильними відповідями (слайд презентації 6)
4. Застосування отриманих знань у стандартних умовах. 30 хв.
Мета. Узагальнити та систематизувати знання студентів про розв’язки показникових рівнянь та нерівностей, формувати уміння та навички застосовувати їх до розв’язання вправ.
Для виконання кожного завдання до дошки виходить один студент з кожної команди. Кожна команда виконує свій варіант у дошки. Студенти, які працюють індивідуально мають можливість контролювати правильність виконання завдання як у себе в зошиті, так і у студента, якій стоїть у дошки.
Завдання. Розв’язати рівняння або нерівність, вказуючи спосіб та властивості які застосовуємо.
|
№ вправи |
І команда |
ІІ команда |
|
1. |
Розв’яжіть рівняння: |
|
|
1) |
|
|
|
2) |
|
|
|
3) |
|
|
|
4) |
|
|
|
5) |
|
|
|
2. |
Розв’яжіть нерівність: |
|
|
1) |
|
|
|
2) |
|
|
|
3) |
|
|
Вправа 3. Робота в парах. Обговоріть і заповніть в зошитах таблицю, яка розподіляє задані рівняння за способами розв’язання
5. Застосування отриманих знань в нових умовах. 5 хв.
Мета. Показати приклади розв’язання показникових рівнянь високого рівня складності.
Завдання. Прокоментуйте дії, які були застосовані при розв’язанні наступних рівнянь
Вправа 1.
Питання до студентів:
- Чим відрізняється це рівняння від тих, що ми з вами розв’язували? (різні основи)
- Який прийом тут застосовують? (поділяють на множник 32х)
- Що цим досягають? (приводимо дане рівняння до однієї основи)
- А далі як проводиться розв’язок? (застосовуємо спосіб заміни змінної)
Питання до вправи 2.
- Як називаеться спосіб розв’язання заданого рівняння? (графічний)
- В чому він полягає? (будуються графіки двох функцій та знаходиться точка їх перетину, абсцисса цієї точки і буде коренем рівняння)
- В нашому випадку чому дорівнює корінь рівняння? (х = -1)
Вправа 2.
Висновок: Для того, щоб розв’язати показникове рівняння або нерівність ми застосовуємо наступні методи:
- Приведення рівняння до однієї основи;
- Винесення загального множника за дужки;
- Застосування властивостей степеня;
- Метод заміни змінної (приведення рівняння до квадратного);
- Графічний метод.
- Систематизація знань, умінь і навичок з теми 2 хв.
Після цього заняття ми повинні знати:
- Означення показникової функції, її властивостей і графіки;
- Методи розв’язання показникових рівнянь та нерівностей.
вміти:
- Розрізняти показникові функції за їх виглядом, графіком;
- Застосовувати властивості показникової функції до розв’язання рівнянь і нерівностей;
- Розв’язувати показникові рівняння та нерівності різними способами.
- Виконання самостійної роботи 15 хв
Завдання. Кожен студент повинен розв’язати не більше двох рівнянь та одну нерівність, якщо розв’яже більше, то зараховується правильно виконане завдання з більшою кількістю балів.
|
№ завдання |
І варіант |
ІІ варіант |
|
1. |
Розв’яжіть рівняння: |
|
|
а) 1 б |
|
а) |
|
б) 1,5б |
|
|
|
в) 2б |
|
|
|
г) 2б |
|
|
|
2. 4б |
Знайдіть найбільший корінь рівняння: |
|
|
|
|
|
|
3. |
Розв’яжіть нерівність: |
|
|
а) 1,5б |
|
|
|
б) 2 б |
|
|
|
4. 3 б |
Обчисліть суму цілих розв’язків нерівності: |
|
|
|
|
|
Самостійна робота оцінюється в 12 балів. Оцінка за самостійну роботу включає в себе:
|
№ з/п |
Найменування контролю знань |
Максимальна кількість балів |
|
1 |
Результат виконання теоретичного зрізу знань |
2 бали |
|
2 |
Виконання самостійної роботи |
6+3= 9 балів |
|
3 |
За активну роботу на занятті |
1 бал |
|
|
Всього: |
12 балів |
- Повідомлення домашнього завдання 3хв.
Розділ VI, § 1, п. 1.3, п. 1.4, с. 249-260, виконати домашню самостійну роботу:
Розв’яжіть рівняння 
.
А) 1; Б) 
; В) -1; Г) інша відповідь.
2. Розв’яжіть рівняння 
.
А) х = 1; Б) х = -1; В) х = 0; Г) інша відповідь.
3. Розв’яжіть рівняння 
.
А) 2; Б) 
; В) -2; Г) інша відповідь.
4. Знайдіть корінь рівняння 
.
А) 
; Б) 4; В) 2; Г) інша відповідь.
5. Знайдіть корені рівняння 
.
А) 5; Б) 2; В) 5 та 2; Г) інша відповідь.
6. Розв’яжіть нерівність: 
А) (0;2); Б) (1; +); В) (-; -1); Г) (-1; 2).
7. Обчисліть суму цілих розв’язків нерівності: 
А) [0; 5]; Б) [1; +); В) (-; 5]; Г) [-1; 2].
Творча робота. Підготувати інформацію про поняття логарифма, історію його виникнення.
Проблемне питання. Яким методом можна розв’язати показникове рівняння 
- Підведення підсумків заняття. 2 хв.
Підводяться результати теоретичного блоку знань та називаються студенти, які заробили на занятті додаткові оцінки та бали
Викладач _________________ Козлова Г.В.
Додаток А
Картка контролю теоретичних знань
студента ________________________________________
І варіант
- Показниковою функцією називається функція _______________________
_______________________________________________________________
-
Підкресліть основні властивості функції
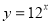
- Область визначення функції:
1)D(y) = (-; 0]; 2) D(y) = (-; 0);
3) D(y) = (-; +); 4) D(y) = (0; +);
- Множина значень функції:
1)E(y) = (-; 0]; 2) E(y) = (-; 0);
3) E(y) = (-; +);4) E(y) = (0; +);
- Функція є:
1) спадною;
2) зростаючою;
3) постійною;
4) ніякою.
ІІ варіант
- Показниковою функцією називається функція _______________________
_______________________________________________________________
-
Підкресліть основні властивості функції
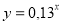
- Область визначення функції:
1)D(y) = (-; 0]; 2) D(y) = (-; 0);
3) D(y) = (-; +); 4) D(y) = (0; +);
- Множина значень функції:
1)E(y) = (-; 0]; 2) E(y) = (-; 0);
3) E(y) = (-; +);4) E(y) = (0; +);
- Функція є:
1) спадною;
2) зростаючою;
3) постійною;
4) ніякою.
Додаток Б
1
про публікацію авторської розробки
Додати розробку