Заняття: Задачі з параметрами.

Заняття

Тема: Задачі з параметрами.

Мета: Використання різних прийомів розв’язування задач з параметрами. Удосконалення навичок розв’язування завдань з параметром різними способами, в тому числі і графічним. Розвиток творчих здібностей учнів при розв’язуванні вправ підвищеної складності

 

Хід заняття:

1.  Орг. момент.

Невідомо, хто, коли, але хтось сказав слова, які передаються нам і які ми передаємо нашим нащадкам:

«Намагайтеся кожного дня  для кожної справи знайти якийсь позитивний початок, оскільки  від того настрою, з яким ви вступаєте в день, або в якусь справу залежать ваші успіхи, а можливо, і невдачі».

Я бажаю вам розпочати заняття  з гарним настроєм і отримати від нього задоволення і гарні результати.

2. Мотивація навчальної діяльності.

Задачі з параметрами відіграють важливу роль у формуванні логічного мислення та математичної культури, але їх  розв’язання викликає значні труднощі. Це пов'язано з тим, що кожна задача з параметрами являє собою цілий клас звичайних завдань, для кожної з яких повинно бути отримано рішення.

 

3. Актуалізація опорних знань

1. Розминка. Усні вправи на використання властивостей деяких рівнянь та нерівностей:

1) ;    2) ;    3);   4);   5);  

6) при яких а      ?

4. Лекційна частина

Якщо в рівнянні (нерівність) деякі коефіцієнти задані не конкретними числовими значеннями, а позначені літерами, то вони називаються параметрами, а рівняння (нерівність) параметричним.

Параметри позначаються першими буквами латинського алфавіту: a, b, c, d, ..., k, l, m, n, а невідомі - літерами x, y, z.

Розв’язати  рівняння (нерівність) з параметрами - значить вказати, при яких значеннях параметрів існують рішення і які вони.

Два рівняння (нерівності), що містять одні і ті ж параметри, називаються рівносильними, якщо:

а) вони мають сенс при одних і тих же значеннях параметрів;

б) кожне рішення першого рівняння (нерівності) є рішенням другого і навпаки.

Розв’язати  рівняння з параметрами - це значить:

1. Вказати, при яких значеннях параметрів рівняння має корені і скільки їх при різних значеннях параметрів.

2. Знайти всі вирази для коренів і вказати для кожного з них ті значення параметрів, при яких цей вираз визначає корінь рівняння.

Можна уявити алгоритм розв'язування такого типу рівнянь.

1. Визначити «контрольні» значення параметра.

2. Вирішити рівняння відносно х, при контрольних значеннях параметра.

3. Вирішити рівняння відносно х, при значеннях, відмінних від «контрольних».

4. Записати відповідь у вигляді:

 

Відповідь: 1) при значеннях параметра ... , рівняння має корені ... ;

2) при значеннях параметра ... , рівняння має корені ... ;

3) при значеннях параметра ... , рівняння коренів не має.

Наведемо алгоритм розв’язання  задач цього типу.

1. Знайти значення параметрів і невідомою, при яких рівняння не має сенсу (якщо, звичайно, такі є).
2. Привести рівняння до стандартного вигляду квадратного рівняння (якщо це необхідно).
3. Знайти «контрольні» значення параметра, що обертаються в нуль коефіцієнт при х2.
4. Вирішити рівняння при цих значеннях а, перевірити, чи всі знайдені коріння відповідають п.1.
5. Знайти «контрольні» значення параметра, що обертаються в нуль дискримінант рівняння і знайти корені рівняння при цьому значенні параметра, після чого перевірити, чи задовольняють вони п.1.
6. Записати корені рівняння при значеннях параметра, для яких D>0, перевірити, чи задовольняють вони п.1.
7. Записати відповідь.

5. Практична частина.

Учитель: пригадаємо  теорію, яка застосовується при розв’язанні  рівнянь виду:  

ах + в = 0   і  ах² + вх + с = 0.

                                                   1.   Розв’язати рівняння:

а) х - а = 0, відповідь: при а (-∞; +∞)    х = а

б) = а    відповідь: при а < 0  коренів немає;

                             при  а = 0  х=0                   при  а ≥ 0   х = ± а

  в) ( а² – 4 ) х = а² + а – 6

   Розв’язок . Якщо   а² – 4 ≠0, т.е. а ≠ ± 2, то  х=; х = =;

                    Якщо  а = 2, т.е.  0х = 0, то х – будь яке число;  

                    Якщо  а = -2, т.е. 0х = -4, то коренів немає;

  г) знайти всі значення параметру   а, при яких рівняння   х⁴ + 3х² + а – 3=0  має один корінь.            Відповідь: а = 3.

Завдання № 3

При якому значенні параметра а система 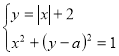  має  3 розв’язки?

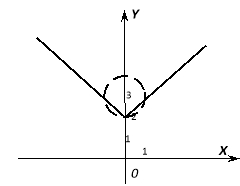          Відповідь: при а = 3.

 

При якому значенні параметра а рівняння має розв’язки?

Розв’язання:

При :  , .

При : 

                         .

Відповідь: при

Завдання (ЗНО) 4

Розв’язати  рівняння:   

Розв’язання:

Заміна: 

 

 

 

  

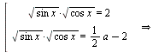
Кути  x – із першої чверті! ⇒   

Відповідь:  ,   

Завдання (ЗНО)  (Самостійна робота)

Знайти всі значення параметру  а, при яких рівняння  має три кореня.

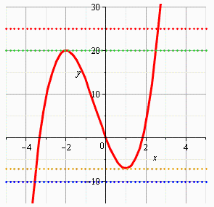
Підказка:   проведіть повне дослідження функції    та накресліть її ескіз.

ФІЗКУЛЬТХВИЛИНКА.  Для розминки пальців

1)      Руки з розведеними пальцями лежать на рівній горизонтальній поверхні. Упродовж 20-30 с перемінно постукувати по столу пальцями то однієї, то другої руки, то обох рук разом;

2)      Руки зігнуті перед собою. Торкатися великим пальцем почергово вказівного, середнього, безіменного, мізинця. Темп виконання і сила натискання поступово наростають. Повторити 5-6 разів;

3)      Імітація кидання м'яча в ціль: двома руками, однією (лівою, правою) своєму ближньому товаришеві; хто знаходиться далеко (з меншою і більшою силою).

 

(Самостійно ) Нехай - корені рівняння . При якому значенні параметра а виконується умова ?

Розв’язання:

                       ,  

За теоремою Вієта: 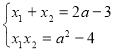,  тому

                                                    Відповідь: при

4) Колективне розв’язання:

При якому значені параметра а нерівність виконується при?

Розв’язання:

При : ,

При :   

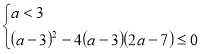
               Відповідь: при 

Завдання:

Знайти всі значення параметру  а, при яких всі розв’язки нерівності   задовольняють нерівності  0 < х < 1.  

Розв'язання

1. Якщо а = 0, то одержуємо нерівність х > 1, яка не задовольняє умову задачі.

2. Якщо а ≠ 0 ,то розгляньмо функцію   Оскільки  при будь-яких значеннях а, то . Тоді  

a)  якщо D = 0, то а=1/2 і нерівність має вигляд  Розв'язком є порожня множина. Але в цьому випадку всі розв'язки заданої в умові нерівності задовольняють нерівність 0 < x < 1. Отже, a = 1/2  задовольняє умову задачі.

б) при a < 0, розв'язок заданої нерівності: , що не задовольняє нерівність 0 < х < 1. в)  при а > 0, умова задачі виконується тільки тоді, коли корінь  буде належати проміжку [0; 1). Маємо. 

Враховуючи ще й випадок а = 1/2, одержуємо, що умова задачі виконується при  

Зауваження. Розв 'язуючи завдання, учень може використати умови розташування коренів квадратного тричлена  відносно чисел а і в.   Відповідь:  

Робота в парах:

1. Зайти всі значення параметру  а, при яких рівняння    х⁴ – 2(а+3)х² + 2а + 9 = 0 має 4 різних кореня.                         Відповідь: а > 0
2. При  яких значеннях параметру  а рівняння  ( 2х – а )log₂х = 0 має рівно один корінь?                         Відповідь: а = 2 или, а ≤ 0

 

Додатково та індивідуально:

№1 Знайти значення параметра, при якому рівняння має єдиний розв’язок:     Відповідь:

№2 Знайти значення параметра, при якому система рівнянь має 3 цілих розв’язки? 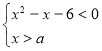   Відповідь:

№3  Знайти значення параметра, при якому система рівнянь має рівно 4 розв’язки? 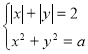     Відповідь:

Завдання для самостійної роботи учнів:

Вправа 1. Вкажіть всі значення параметра , за яких графіки функцій і мають тільки дві спільні точки.   Відповідь. .

Вправа 2. Знайдіть найбільшеціле значення параметра а, за якого

система нерівностей немає розв’язків.   Відповідь. .

Вправа 3. В залежності від значення параметра а розвяжіть рівняння

.  

Відповідь. Якщо : розв’язків немає;  

якщо            якщо

6. Підсумки заняття.

«Сніжна грудка».   Слово – речення – питання – відповідь.

Перший учень проговорює слово, що стосується даної теми, другий складає речення з цим словом, третій складає питання до цього слова, а четвертий відповідає на нього.

7. Рефлексія.

Прийом «Комплімент»: Мета даного прийому - оцінити свою активність і якість роботи. Учні оцінюють внесок один одного в урок і дякують один одного (Комплімент-похвала, Комплімент діловим якостям, Комплімент в почуттях) і вчителі за проведений урок. Такий варіант закінчення уроку дає можливість задоволення потреби у визнанні особистісної значущості кожного.

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ

1. Програма для загальноосвітніх навчальних закладів «Математики», МОН України, ст.. 24-28, 67-72
2. П.І. Горнштейн «Задачі з параметрами», Київ, РІА «Текст», 1992
3. Є.А.Єфімов, Л.В.Коломієць, Задачі з параметрами, навчальний посібник для факультету довузівської підготовки, Самара, 2006
4. Т.С. Непочатова, І.О. Сіренький, Г.С. Смішко «Математичні олімпіади Хмельниччини»,  інформаційний вісник ХОІППО, 2009
5. Науково-методичний журнал «Математика в школах України