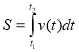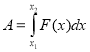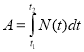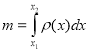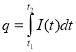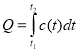Застосування інтеграла

Інтегрований урок математики та фізики

 

Тема: Застосування інтеграла при розв’язувані задач з фізики

Мета:

сприяти глибокому засвоєнню знань фізики і математики через встановлення міжпредметних зв’язків засобами інтегрального числення, формувати практичні зв’язки наукового розуміння законів, взаємозв’язків явищ у природі за допомогою розв’язування задач; розвивати в учнів вміння узагальнювати цілісну систему, вміння реалізувати практичні зв’язки курсів математики і фізики, розвивати навички самостійного прийняття рішень, виховувати культуру розумової праці, створювати сприятливі умови для формування загальнонавчальних умінь і навичок учнів.

 

Тип уроку: застосування знань, умінь та навичок.

 

Обладнання: плакати, тексти задач для розв’язання на уроці, , графопроектор, кодопозитиви, портрети Архімеда, Ньютона, Лейбніца

 

Епіграф уроку:

Не досить оволодіти премудрістю, потрібно також уміти користуватися нею.                                                                                                                                                                        Цицерон

 

Хід уроку

І. Організаційна частина

Привітання . Перевірка готовності класу до уроку.

ІІ. Мотивація навчальної діяльності

Учитель математики.

Математика вивчає різні зв’язки між величинами. Найважливіші приклади таких зв’язків дає механічний рух. Між положенням точки (її координатою та її швидкістю) є відомий зв'язок, який лежить в основі математичного аналізу: швидкість є похідна від координати за часом: . Сама операція знаходження швидкості називається диференціюванням. Розв'язування оберненої задачі – находження положення точки за її швидкістю – приводить до поняття первісної функції і розв’язується за допомогою іншої математичної задачі, яка називається інтегруванням.

Вчитель фізики

Ви знаєте багато прикладів пар величин, які пов’язані між собою так само, як положення точки та її швидкість. Знаходження однієї з величин, якщо відома друга, ми зводили до операції диференціювання. Так, лінійна густина тонкого стержня є похідна від його маси за довжиною, потужність є похідна від роботи за часом, сила струму є похідна заряду за часом і т.д.

Перед тим, як перейти до розв’язування прикладних задач на застосування інтеграла, ще раз повернемось до задачі про механічний рух.

Нехай точка рухається зі сталою швидкістю . Графіком швидкості в системі координат буде пряма , паралельна осі часу (Мал.1). Якщо вважати, що в початковий момент часу точка знаходилася в початку координат, то її шлях , пройдений за час , обчислюється за формулою . Величина являє собою площу прямокутника, обмеженого графіком швидкості, віссю абсцис та двома вертикальними прямими, тобто шлях точки можна обчислити як площу під графіком швидкості.

    

 

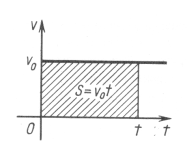
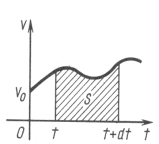
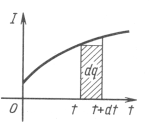
Мал.1     Мал.2      Мал.3

 

Звернемось до випадку  нерівномірного руху. Тепер швидкість можна вважати сталою тільки на маленькому відрізку часу. Якщо швидкість змінюється за законом , то шлях, пройдений точкою за проміжок , наближено дорівнює добутку , а на графіку – площі прямокутника зі сторонами і Точне значення шляху за проміжок часу дорівнює площі криволінійної трапеції, що заштрихована на малюнку (Мал.2). Весь шлях дорівнює сумі площ всіх таких криволінійних трапецій, тобто дорівнює площі під графіком швидкості.

Аналогічно якщо ми накреслимо графік залежності сили струму від часу , то величина заряду, який буде перенесено струмом за проміжок часу , наближено обчислюється за формулою , тобто дорівнює площі прямокутника зі сторонами і (Мал.3). Точне значення величини заряду можна обчислити як площу під графіком сили струму.

 Таким чином задача інтегрування тісно пов’язана з задачею обчислення площі.

Вчитель математики:

 Ви знаєте, що задача обчислення площі під графіком функції – площі криволінійної трапеції – тісно пов’язана з інтегралом. Можна про інтеграл коротко сказати так: Інтеграл – це площа.

 Нагадаємо хід міркувань, застосованих для обчислення площі криволінійної трапеції. Відрізок під графіком функції (неперервної та невід’ємної на цьому відрізку) розбивають на частин. Площа криволінійної трапеції всього підграфіка розбивається на суму площ менших криволінійних трапецій. Кожну таку трапецію можна наближено вважати прямокутником. Сума площ тим точніше дає уявлення про площу криволінійної трапеції, чим більше буде частин, на які розіб’ється відрізок ( Мал.4)

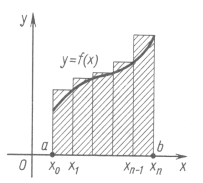
Мал.4

 За допомогою формул це можна записати так.

Відрізок розбито на частин точками , довжину -го відрізка позначимо . Сума виражає наближено площу східчастої фігури (Мал.4).

Суми виду називають інтегральними сумами для функції . Площа під графіком дорівнює границі інтегральних сум, якщо діаметр розбиття – найбільша з довжин відрізків, - прямує до нуля. Таким чином про інтеграл можна сказати так:

Визначений інтеграл дорівнює границі інтегральних сум функції:

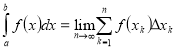
Розглянутий спосіб обчислення площ походить з далекої давнини. Ще в ІІІ ст. до н.е. великий Архімед обчислив площі параболічного сегменту за допомогою винайденого ним «методу вичерпування», який за дві тисячі років був перетворений на метод інтегрування. Архімеду вдалося виконати пряме обчислення деяких площ, а отже і інтегралів. Але лише у ХVII столітті Ньютону та Лейбніцу вдалося відкрити загальний спосіб обчислення  інтегралів.

Раніше нами було розглянуто доведення теореми, що швидкість зміни функції змінної площі під графіком функції дорівнює функції, тобто .

Відома теорема Ньютона – Лейбніца, яка носить прізвища засновників математичного аналізу, стверджує:

Нехай - дана неперервна на відрізку функція , а - одна з її первісних, то .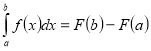

Теорема Ньютона – Лєйбніца зводить обчислення інтегралів до обчислення первісних.

«Метод вичерпування» Архімеда хоча і не дав загального способу обчислення площі, однак зіграв дуже велику роль в математиці, оскільки за його допомогою вдалося об’єднати різні задачі – обчислення площі, об’єму, маси, роботи, тиску та інших.

Вчитель математики

 Таким чином, при знайомстві з інтегралом ми виділили три його характеристики.

1. Інтеграл від функції 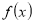є площа під графіком (з урахуванням знаку).
2. Інтеграл є границя інтегральних сум.
3. Інтеграл від функції 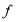є приріст її первісної.

Будь-яка з цих характеристик інтегралу може слугувати основою для його застосувань. Найбільш стандартним шляхом вираження однієї величини як інтеграл від іншої є використання третьої характеристики інтеграла як приросту первісної. Але і дві перші характеристики дуже важливі в застосуванні, так як дозволяють отримати геометричний зміст зв’язку між фізичними величинами та простий спосіб їх наближеного обчислення.

Інтеграл застосовується тоді, коли відома швидкість (густина) шуканої величини. Якщо шукану величину подати у вигляді приросту деякої функції , то є похідною для , а отже є первісною для , тобто інтеграл від функції .

Запишемо тепер все це за допомогою формул. У якості незалежної змінної виберемо літеру . Нехай ми шукаємо величину . Розглянемо її значення на маленькому відрізку . Нехай швидкість зміни величини позначено . Цей зв'язок між величинами і можна записати у диференціальній формі:

  (або )

(Нагадаємо, що )

Тоді

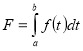
Повернемося до величин , які можна обчислювати за допомогою інтеграла. До таких величин можна віднести переміщення, роботу, масу, електричний заряд, тиск, теплоту. До них можна приєднати і геометричні величини – довжину, площу, об’єм.

Вчитель фізики

пропонує учням прокоментувати таблицю фізичних величин та співвідношень між ними.

 

№ пп	Величини	Співвідношення	Знаходження похідної	Знаходження  інтеграла
1	S – переміщення v -- швидкість
2	A - робота F - сила
3	A - робота N -  потужність
4	m– маса тонкого  стержня - лінійна густина
5	q– електричний заряд I – сила струму
6	Q – кількість теплоти c- теплоємність

 

ІІІ. Застосування знань та умінь

Вчитель фізики

Розглянемо приклади задач фізичного змісту, для розв’язання яких доцільно використати інтеграл.

(Вчитель математики контролює правильність математичних дій)

Задача 1

При якій висоті рідини в циліндричній посудині радіусом сила тиску на дно посудини та на бічну стінку будуть однаковими?

Розв’язання

Тиск рідини на стінки посудини Р= ρgһ, відповідно, сила тиску дорівнює . Тиск на бічну стінку залежить від глибини у: Р(y) = ρgy. Розіб’ємо подумки бічну стінку на кільцеві смужки висотою dy, тоді сила тиску смужки на глибині dF(y)= ρgy2πrdy. Повна сила знаходиться інтегруванням по всім кільцям:

F₂  = dF(y) = ρg2πr ydy = πρgrһ² .

З умови F₁ = F₂ отримуємо = r.

Задача 2

До стелі ліфта, що вільно падає, прикріплено пружину з важком. Важок не коливається. Знайти максимальне значення сили пружності при миттєвій зупинці ліфта, якщо безпосередньо перед зупинкою ліфта сума потенціальної енергії важка дорівнювала 40 Дж. Коефіцієнт жорсткості пружини 500 Н/м. Тертям та масою пружини знехтувати. Потенціальну енергію сили пружності і сили тяжіння відраховувати від положення максимального розтягу пружини.

Розв’язання

Згідно формули для роботи рівнодійної сили  Е_k - Е_k0  = А_mg – А_пружн

Так, як А_mg = mgx_max =Е_п0,  тобто, початковій потенціальній енергії важка, а

А_пружн = = = .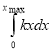

Тоді маємо    -Е_k0  = Е_п0 - ,

 тобто повна енергія

Е_повн = Е_k0 + Е_п0 = . звідки

F_пружн = 200 Н

 

Задача 3

Температура маси m ідеального газу з молярною масою М змінюється за законом Т = αV², де α – відома стала. Яку роботу виконує газ при збільшенні його об’єму від V₁ до V₂? Чому дорівнює зміна внутрішньої енергії газу в цьому процесі? Отримує чи віддає газ тепло в цьому процесі?

Розв’язання

Скористаємось рівнянням стану ідеального газу: 

Роботу можна знайти методом інтегрування:

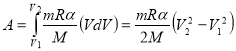
Для визначення внутрішньої енергії скористаємось формулою

,

Отже,

Згідно першого закону термодинаміки , теплота, надана тілу в цьому процесі, дорівнює д

> 0,

 отже газ отримує теплоту.

 

Задача 4

Над ν = 2 молями ідеального газу здійснюється цикл 1234(див рис),

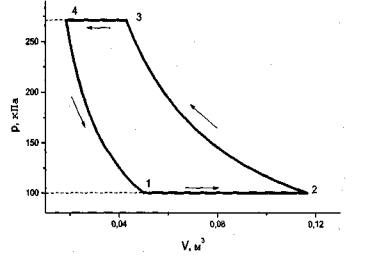
Який складається із двох ізобар(12, при тиску Р₁=100 кПа, та 34, при тиску Р₃=272 кПа) та двох ізотерм (23, при температурі Т₂= 700 К, та 41, при температурі Т₁= 300 К).Знайти теплоту, яку газ поглинає за цикл.

 

Розв’язання

Згідно першого закону термодинаміки, Q = ∆U +А. В коловому процесі зміна внутрішньої енергії дорівнює нулю, отже Q = А. на ізобарах 12 і 34 робота дорівнює

А₁₂ = Р₁ (V₂  - V₁), А₃₄ = Р₃ (V₄  - V₃),

 або враховуючи рівняння стану в точках 1234

Р₁V₁ = Р₃V₄  = νRT_1,

Р₁V₂ = Р₃V₃  = νRT₂

отримуємо   А_{12  +} А₃₄  = 0

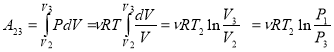
Аналогічно,

,

Отже,

< 0

Підстановка даних із умови задачі дає Q = -3,32 кДж, теплота віддається, а не поглинається, тобто , в цьому циклі теплова машина працює як холодильник.

 

Задача 5

Заряджений конденсатор ємності С замкнений на котушку індуктивності L. Знайти таку залежність від часу ємності конденсатора, при якій струм у колі збільшується прямо пропорційно часу. Електричним опором кола знехтувати.

Розв’язання

 За законом Фарадея, , так як за умовою задачі струму колі збільшується прямо пропорційно часу:. отже, і напруга на конденсаторі, що дорівнює напрузі на котушці в будь – який момент часу, теж залишається сталою:

,

де - початковий заряд на конденсаторі, - заряд, який стік із обкладок конденсатора за час t , а C - ємність конденсатора в момент t. З рівності знаходимо струм:

• 

 Тоді повний заряд, що стікає з конденсатора за час дорівнює

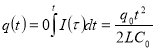
 Підставивши цей вираз для заряду у формулу, отримуємо

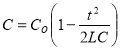
 Зауважимо, що ця відповідність буде правильною за умови, що q < q_0.

 

Задача 6

 Дві частинки, які мають масу 5 мг, 2 мг і заряди, що дорівнюють +12 нКл та + 7 нКл, рухаються назустріч одна одній, маючи вдалині відносну швидкість 18 км/год. На яку найменшу відстань зблизяться частинки?

Розв’язання

 Задачу можна розв’язати трьома способами, враховуючи вибір системи відліку:

1) (ІСВ) – інерціальна система відліку(пов’язана з Землею);

2) система відліку, яка зв’язана з центром інерції системи двох частинок;

3) НІСВ – неінерціальна система відліку, тобто одна частинка нерухома, а інша рухається назустріч першій з відносною швидкістю (v_відн)

 Розглянемо третій спосіб. Виберемо систему, яка рухається поступово разом з однією із заряджених частинок, наприклад, з першою. Ця система – неінерціальна. У ній перша частинка нерухома, а друга рухається назустріч першій з початковою швидкістю (v_відн). Система вважається незамкненою, оскільки на неї діють сили інерції, які потрібно вважати зовнішніми відносно системи.

Але ми знаємо, що зміна енергії системи дорівнює роботі (А) сили інерції (F_ін), що діє на частинку (m₂) під час її наближення до частинки (m₁).

, де W₂ – кінцева енергія, при r = r_min, яка дорівнює потенціальній енергії кулонівської взаємодії, тобто

;

,

Оскільки в момент найбільшого зближення друга частинка має нульову швидкість. W₁-початкова енергія системи частинок, яка дорівнює кінетичній енергії другої частинки

А – робота сили інерції, визначається за допомогою інтеграла

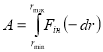
Врахувавши, що , де F – кулонівська сила.

Знаючи , тоді

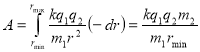, вважаючи.

Прирівняємо роботу зі зміною енергії:

Частинка зблизиться на мінімальну відстань 4 см.

 

Задача 7

Магнітне поле створюється провідником зі струмом, сила якого 50 А.У полі розміщена рамка. Так що дві  великі сторони довжиною 65 см паралельні провіднику, а відстань від провідника до найближчої сторони рівна її ширині. Який магнітний потік пронизує рамку?

 

Розв’язання

Магнітна індукція поля провідника визначається:

, де r – відстань до провідника.

Магнітний потік що пронизує рамку визначається за законом:

, де , а B- зменшується з віддаленням від провідника. Розіб’ємо площу рамки на окремі ділянки, елементарна площа яких. Для визначення магнітного потоку звернемось до процесу інтегрування:

;

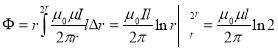Підрахунки дають значення 4,5 мкВб.

 

ІV. Підведення підсумків

На уроці було систематизовано знання щодо застосувань інтегралу при розв’язуванні прикладних задач. Розглянуто схему застосування інтегралу (алгоритм переходу до інтегралів) при розв’язуванні задач фізичного змісту.

Фізика вивчає залежності між величинами та описує їх мовою математики; математика систематизує та узагальнює способи розв’язування різноманітних задач, створюючи математичні моделі та методи їх дослідження.

 

Сила і загальність методу диференціального й інтегрального числення такі, що не ознайомившись з ними, не можна як слід зрозуміти все значення математики для природознавства і техніки і навіть оцінити всю красу і принадність самої математичної науки.

          А.М.Колмогоров

V. Домашнє завдання

ШкільМ.Т. та ін. Алгебра та початки аналізу: Підруч. для 11 класу загальноосвітніх навч. закладів /М.І.Шкіль, З.І.Слєпкань, О.С. Дубінчук. – К.: Зодіак – ЕКО, 2006

Опрацювати за підручником с.144- 148. Виконати вправи № 66(1,3), № 67-71.