Відділ освіти, молоді та спорту 

 Новоушицької ОТГ 

Песецька загальноосвітня школа І – ІІ ступенів

 

Сіваш В.В.

Сіваш Р.І.

 

 

Застосування інтерактивних  форм і методів роботи 

на уроках математики і фізики  як запорука формування високої

пізнавальної активності учнів

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Песець -2018 р.

Упорядники:

 

Сіваш Валерій Вікторович – фізики, математики та інформатики   Песецької ЗОШ І-ІІ ступенів.

Сіваш Раїса Іванівна – вчитель математики Песецької ЗОШ І-ІІ ступенів

 

 

 

 

 

 

Рецензенти: Олександр Іванович,  методист Новоушицького МК

 

 

 

 

Застосування інтерактивних форм і методів роботи на уроках математики і фізики як запорука формування високої пізнавальної активності учнів – Песець – 2018 р. – 69 с.

 

      Посібник складений відповідно до чинної програм з фізики та математики для загальноосвітніх навчальних закладів за новим Державним стандартом. Видання містить інтерактивні форми і методи викладання, конспекти уроків, різнорівневі задачі, тестові завдання для тематичного оцінювання. У посібнику описані вікторини, розв’язки задач, практичні роботи і демонстраційні досліди; подано додатковий матеріал, який учитель може включити в урок, використовувати підчас проведення занять, на виховних та позаурочних заходах , або факультативах. 

         У розробках уроків використовуються        інтерактивні методики             навчання          та      інші   прогресивні         педагогічні технології.            

Посібник призначений для вчителів фізики та математики.

Зміст

1.   Вступ ……………………………………………………………...……. 4

2.   «Навчаючи когось – навчайся сам» ………………………….………..6

                    2.1 Дільники і кратні  ………………………………...……..………..6

3.   Розглянемо деякі ігри ………………………………..………………..15

1.   Гра «Акваріум».   ………………………………………….…..…. 15

2.   Гра «Математичний дощик»………………………….………..15

3.   Гра «Цукерочки»……………………………………………..……15

4.   Гра «Збираємо грибочки у лісі». ……………………….……...15

5.   Гра «Зоряне небо». …………………………………………….…16

6.   Гра «Йдемо по стежинці».  ……………………………..….....16

7.   Гра «Кущик, що цвіте». …………………………………………16

8.   Гра «Математичний футбол». ……………………………….17

9.   Гра «Цікаві квадратики». ……………………………………...17

4.   Приклади використання інтерактивних технологій на уроках фізики

та математики ……………………………………………………………….…21

                      Теорема Піфагора …………………………………………..…..21

5.   Позакласні заходи …………………………………………………..…32

6.   Усний журнал …………………………………………………….……40

7.   Конспекти уроків фізики ………………………………………...……49

8.   Література ………………………………………………………..……69

Вступ

 «Учень - не посудина, яку треба наповнити, а смолоскип, який треба запалити!»

Людина - це саморозвивальна система, що все пропускає через своє усвідомлення і свою душу. Згідно із цим твердженням мають змінитися ціннісні орієнтації вчителя і сучасної школи.

Сучасна школа вимагає докорінного переосмислення процесів навчання і виховання, застосування перспективних технологій, створення умов для самонавчання, саморозвитку і самореалізації особистості учня.

На перший план виступає розвиток творчого потенціалу дитини, розкриття індивідуальних, самобутніх Ті здібностей.

«НОВА ШКОЛА КЛАДЕ СОБІ ЗА МЕТУ ЗДОБУТИ, ДАТИ

ВИЯВИТИСЯ САМОСТІЙНИМ ТВОРЧИМ СИЛАМ ДИТИНИ»

(Софія Русова)

У сучасному суспільстві навчання можна організувати так, що джерелом знань виступатиме не тільки вчитель, а й комп'ютер, телевізор, відео. Учні відповідно, повинні вміти осмислювати отриману інформацію, трактувати її, застосовувати в конкретних умовах; разом з тим думати, розуміти суть речей, уміти висловлювати свою власну думку. Саме цьому сприяють інтерактивні технології навчання. Перевагою інтерактивних технологій навчання є те, що учні застосовують усі рівні пізнання (знання, розуміння, застосування, оцінка), збільшується в класах кількість учнів, які свідомо засвоюють навчальний матеріал. Учні займають активну позицію в засвоєнні знань, зростає їхній інтерес в одержанні знань. Значно підвищується особистісна роль учителя-він виступає як лідер, організатор. Але треба зазначити, що проектування і проведення уроку за інтерактивними технологіями вимагають передусім компетентності в даних технологіях учителя , його вміння переглянути й перебудувати свою роботу з учнями. Для того, щоб учень добре навчався , він повинен постійно бути включений у процес навчання шляхом спілкування з учнями, учителем, він має говорити на уроці не один раз і не два, а постійно спілкуватися. Саме учень повинен стати центральною фігурою на уроці. Від творчої активності учнів їхнього вміння доказово міркувати , обґрунтовувати свої думки, уміння спілкуватися з учнями класу ,з учителем залежить результативність уроку.

Своє завдання, як вчителя,вбачаю у організації навчального процесу таким чином, щоб допомогти учням засвоїти базові знання; навчити методики здобуття нових знань; допомогти шукати себе кращого; створити умови для вільного самовизначення, для розвитку самостійної творчості особистості.

Для реалізації основної формули педагогіки життєтворчості особистості «Допоможи мені зробити це самому!» застосовую інноваційні технології навчання, виховання і розвитку.

Найкращий результат в навчанні дають такі методи:

1 .Навчання з демонстрацією, експериментами - ЗО %;

2.           Навчання        в малій групі під час дискусії - 50 %;

3.           Навчання        під час роботи в групі 75 %;

4.           Навчання        одним учнем іншого - 90%;

«НАВЧАЮЧИ КОГОСЬ - УЧУСЯ САМ!»

Інноваційні методи спрямовані на те, щоб не давати готових відповідей, а націлювати учнів на творчий пошук, на формування власної думки.

Пропоную деякі форми роботи, які допомагають виховати цікавість і актуалізувати пізнавальну діяльність учнів на уроках математики.

 

АКТУАЛІЗАЦІЯ.

Велике значення має організаційний момент кожного уроку. Як правило, вдало обраний вид діяльності учнів на початку уроку налаштовує їх на плідну роботу протягом усіх 45 хвилин.

1 .Можна провести етап актуалізації у вигляді математичної зарядки.

Заздалегідь готуються декілька картинок із найпростішими прикладами.

Приклади      подаються з        відповідями.        Кожна         вправа        зарядки складається із двох рухів. Учитель по черзі показує класу картки, а учні у відповідь роблять певний рух. Наприклад: якщо відповідь правильна - руки вгору, неправильна - руки вперед. Зарядка може складатися із 2-3 вправ. Складання комплексів вправ можна доручити дітям.

Комплекс математичної зарядки з теми «Дільники і кратні».

Дільники і кратні

 

Остача при діленні числа 30 на 5 дорівнює 0.

Дійсно, 30 = 5 · 6.

У такому випадку будемо говорити, що число 30 ділиться націло на 5.

                                          30 = 5 · 6.

Число 5 називають дільником числа 30,

а число 30— кратним числа 5.

Зауважимо, що число 30 не ділиться націло на 7. Тому 7 не є дільником числа 30, а число 30 не кратне числу 7. Числа 1, 2, 3, 6, 10, 15, 30 також є дільниками числа 30, а число 30 є кратним кожного з цих чисел.

 Якщо натуральне число а ділиться націло на натуральне число b, то число а називають кратним числа b, число b— дільником числа а.

Запишемо всі натуральні числа, на які ділиться число 18. Такими числами є 1, 2, 3, 6, 9, 18. Отже, число 18 має 6 дільників: 1, 2, 3, 6, 9 і 18.

Число 1 має лише один дільник — 1. Будь-яке інше число, наприклад, 23, обов’язково має принаймні два дільники — число 1 і саме число 23, до того ж, 1 — найменший дільник, саме число 23 — найбільший.

 

 

А як краще говорити: «Число а ділиться націло на число b», «Число b є дільником числа а», «Число а кратне числу b», «Число а є кратним числа b»?

 

            

 Байдуже, будь-який вибір буде правильним.

 Дуже легко записати всі дільники числа 6. Це числа 1,2, 3 і 6.

 А чи можна перелічити всі кратні числа 6?

Зрозуміло, що числа 6 · 1, 6 · 2, 6 · 3, 6 · 4, 6 · 6 і т.д. кратні 6. Отже, чисел, кратних 6, безліч.

 

Взагалі, для будь-якого натурального числа а кожне із чисел а · 1, а · 2, а · 3, а · 4,... є кратним числа а.

 

УВАГА!

Число 1 – дільник будь-якого натурального числа, оскільки будь-яке число ділиться на 1 без остачі.

Найменшим дільником будь-якого натурального числа а є число 1, а найбільшим — саме число а.

Серед чисел, кратних а, найбільшого немає, а найменше є — це саме число а.

Кожне з чисел 21 і 36 ділиться націло на 3. Сума цих чисел 21 + 36 також ділиться націло на 3.

Взагалі, якщо кожне з чисел а і b ділиться націло на число к, то і сума а + b також ділиться націло на число к.

 

Число 35 ділиться націло на число 7, а число 17 на число 7 не ділиться націло. Сума 35 + 17 націло на 7 також не ділиться.

Взагалі, якщо число а ділиться націло на число к, а число b не ділиться націло на число к, то сума а + b також не ділиться націло на число к.

 

 

Приклад 1

Напишіть усі дільники числа 24.

Розв’язання

    Число 24 ділиться націло на числа 1, 2, 3, 4, 6, 8, 12, 24, оскільки 

1   · 24 = 24,

2   · 12 = 24,

3   · 8 = 24,

4   · 6 = 24, 6 · 4 = 24,

8 · 3 = 24,

12 · 2 = 24, 24 · 1 = 24.

  Отже, дільниками числа 24 є числа 1, 2, 3, 4, 6, 8, 12, 24.

  Відповідь. 1, 2, 3, 4, 6, 8, 12, 24.

    Приклад 2

  Напишіть три числа, які кратні числу 6.

  Розв’язання

  Числа 6, 12, 36 кратні числу 6, оскільки

6 · 1 = 6,  6 · 2 = 12,  6 · 6 = 36.

  Відповідь. 6, 12, 36

    Приклад 3

  Напишіть усі значення х, що кратні числу 4 і при яких буде правильною нерівність 18 < х < 36.

Розв’язання   18 < х < 36    х = 20; 24; 28; 32.

  18 < 20 < 36,   18 < 24 < 36,

  18 < 28 < 36,   18 < 32 < 36.

  Відповідь. х = 20; 24; 28; 32.

На другому етапі уроку відбувається усвідомлення нової інформації та ідей; На цій фазі навчання вчитель якнайкраще впливає на учнів, а вони підтримують свою           зацікавленість      роботою.    На     етапі рефлексії передбачається, що учні перетворюють отримані знання у своє власне бачення,         починаючи           висловлюватися, використовуючи нові   ідеї, обмінюються думки одне з одним, формуючи свою точку зору.

На уроці створюються умови для забезпечення власної навчальної діяльності школярів, забезпечується інтерактивне спілкування між дітьми.

У своїй роботі та на своїх уроках я використовую такі інтерактивні           методи        навчання,   як      парна          групова      робота (кооперативне навчання) та колективно-групова робота.

За словами А. Маслоу, в людини переважають дві потреби - потреба до постійного росту й потреба бути в безпеці. Один з найважливіших способів досягнення безпеки - це поєднатися з іншими людьми, залучити до групи; це дає учням змогу подолати труднощі, які постають на їхньому шляху, і відчути підтримку, яка дає можливість вийти далеко за межі їх нинішнього рівня знань і вмінь.

Під час кооперативного навчання важливими компонентами роботи є:

•   позитивна взаємозалежність: один не може бути успішним, якщо не будуть успішними всі;

•   особистісна взаємодія, що стимулює діяльність: усне пояснення того, як розв'язувати проблеми, передача друзям власних знань, перевірка розуміння та обговорення досліджуваних понять, поєднання нового матеріалу з вивченим;

•   індивідуальна та групова підзвітність: група несе відповідальність за досягнення своїх цілей, і кожен член групи відповідає за свою частину роботи, а кожна особа встановляє, хто більше потребує допомоги і підтримки в ході навчання;

•   розвиток навчання міжособистісного спілкування і спілкування в невеликих групах;

•   обробка (аналіз) даних про роботу в групі.

Робота в групах і парах може бути організована як на уроках засвоєння, так і на уроках застосування знань, умінь та навичок, бути частиною повторювально-узагальнюючого уроку. Серед видів кооперативного навчання може бути:

1. Робота в парах, завдяки якій усі учні класу отримують можливість говорити, висловлюватись. Учні мають час подумати, обмінятися думками з партнерами, а потім уже озвучувати свої думки перед класом.

Під час роботи в парах можна швидко виконати такі вправи:

•   обговорити короткий текст, завдання;

•   сформувати підсумок уроку;

•   розробити разом питання до вчителя чи до інших учнів класу;

•   проаналізувати вправу чи задачу;

•   протестувати та оцінити один одного;

•   дати відповіді на запитання вчителя;

•   порівняти записи зроблені в класі.

Об'єднуючи учнів у пари, потрібно за заздалегідь визначити, хто з них буде висловлюватись першим, та встановити час на висловлювання кожного в парі та спільне обговорення, по закінченні часу кожна пара має представити результат своєї роботи.

2.                       Робота в малих групах, завдяки якій можна розв'язати складні проблеми, що потребують колективного розуму. Кожна група повинна виконати своє завдання та представити результати роботи. У групі повинні бути розділені ролі, кожен має відповідати за свою частку роботи. Висловлюватись повинні всі по черзі, не перебиваючи один одного, утримуючись від оцінок та образ учасників групи та врешті дійти до спільної думки.

Різновидом роботи в малих групах, які я використовую у своїй роботі, є така інтерактивна вправа, як «Пошук інформації». Потрібна тоді, коли необхідно доповнити те, що пояснив учитель, або доповнити інформацією, потрібної для виконання домашнього завдання, або

якщо після лекції вчителя потрібно дати відповіді на запитання.

Джерелами пошуку інформації можуть бути: роздатковий матеріал, підручник, довідкова література, таблиці тощо.

3.                       Серед видів колективно-групового навчання у своїй роботі я використовую такі інтерактивні вправи:

«Мікрофон». Це технологія загально групового обговорення, яка надає можливість кожному сказати щось швидко, по черзі, відповідаючи на запитання або висловлюючи свою думку.

Робота може бути організована так:

•       Клас ставить запитання (кілька запитань).

•       Ручка (олівець тощо) виконує роль уявного мікрофона, який учні передають один одному, по черзі беручи слово.

•       Слово має тільки той, у кого в руках «уявний» мікрофон.

•       Кожен має говорити швидко і логічно.

Така технологія застосовується мною дуже часто на етапі актуалізації опорних знань учнів або під час підбиття підсумків уроку.

 «Мозковий штурм». Це технологія колективного обговорення, яка використовується для вироблення розв'язання проблеми.

Мозковий штурм спонукає учнів проявити творчість та уяву, дає можливість вільно висловлювати свої думки. Мета цієї технології полягає в тому, щоб за обмежений час вислухати якомога більше ідей учнів.

Застосовується ця інтерактивна вправа під час розв'язання задач із стереометрії, особливо таких, де потрібно вміти розв'язувати кілька ВП простих планіметричних задач.          

Ще одним важким питанням у разі застосування інтерактивних технологій на уроках математики є питання оцінювання учнів. Оскільки, крім традиційних критеріїв оцінювання, треба дати такі критерії, які б оцінювали вміння відстоювати свою думку, дати чітку аргументацію своєму викладачу з певного питання.

Тому серед способів оцінювання, які я застосовую на своїх уроках, можна запропонувати такі:

1)                      Експрес-опитування - стислі письмові або усні відповіді (наприклад, за допомогою технології «Мікрофон» (усно), графічний диктант, диктант «Закінчити висловлення»), результати яких учні в парах перевіряють самостійно прямо на уроці та виставляють один одному оцінки (від «1» до «12» балів),математичний диктант, під час якого за формулами необхідно виконати деякі обчислення та перевірити їх результати тощо.

2)                      Тест - завдання, до кожного з яких пропонується 4 варіанти відповіді, а учні повинні вибрати з них одну - правильну. Під час уроку аркуші, на яких учні дали відповіді на запитання тесту, збираються і знову роздаються іншим учням, усі разом обговорюємо правильні відповіді, одночасно перевіряючи аркуші своїх однокласників.

3)                      Фронтальне опитування - це докладне опитування учнів з теорії (наприклад, на доведення теореми), де потрібно дати чітке обґрунтування теми, наводячи конкретні приклади для ілюстрацій своєї відповіді (частіше з алгебри). Під час таких відповідей усі учні класу слідкують за поясненням І мають змогу задавати додаткові запитання.

Іноді доведення теореми ми проводимо всім класом, слідкуючи за логічною побудовою теореми, продовжуючи один одного.

4)                      Самостійна або контрольна робота, яка може тривати весь урок або його частину.

5)                      Спостереження оцінювання учня під час роботи в групі, висування учнем ідей за «мозкового штурму», залежить від поведінки учня, його активності, внеску в роботу групи, узагальнень збоку учня.

6)                      Самооцінка, оцінка в парах.

Поряд з цим, учням потрібно учити не тільки самостійно розв'язувати вправи та задачі, а й складати їх самостійно. Самостійність мислення - це один з особливих моментів вивчення математики.

Ігри розподіляються по віку. У 5 -6 класах простіші і більш казкові, у 7-8 класах - складніші, які приводять до чітких міркувань. Ігри, що використовуються в 9-х класах мають сприяти розвитку мислення, мобілізувати учнів до глибокого розуміння матеріалу, що сприяє активізації розумової діяльності. Отже, ігри пов'язують, наближують учнів до життєвих ситуацій, розвивають швидке мислення, зорову спостережливість. Малюнки до них та відповідний матеріал вчителю можуть допомагати підготовляти учнів. Це також розвиває їхню уяву. На перший погляд, частина ігор здається простими і подібними. Але зірки на небі і краплинки, що падають з хмаринки, грибочки в лісі показують в учням різноманітність використання математичних знань. В ігри можуть грати як дві команди, так і учні. 

Розглянемо деякі ігри

1.     Гра «Акваріум».

На малюнку намальовані «акваріум» і рибки, що живуть у ньому (п'яти - шести видів, в залежності від кількості різноманітних завдань). Грає дві команди. Вони вибирають одну рибку кожного виду.

На тильній стороні однакових рибок записуємо завдання одного типу. Після правильного його розв’язання команда забирає рибку собі. Яка команда «наловила» більше рибок - та і виграла. Якщо гравець не може дати відповідь, йому допомагає команда.

2.     Гра «Математичний дощик».

На ватмані намальовані хмаринки, а з них падають краплинки дощу, їх прикріпляють до ватману, а на зворотній стороні записують завдання відповідної складності: білі - це прості, голубі - трохи складніші, а сині - це найскладніші. Кожна краплинка приносить бали: біла -1 бал, голуба - 2 бали, синя - З бали. Команда, що одержала найбільше балів, перемагає.

3.     Гра «Цукерочки».

Намалюємо конфетки різних видів та на тильній стороні запишемо завдання. Однаковим цукерочкам відповідають подібні завдання. Учні вибирають різні конфетки - завдання і виконують їх. Якщо завдання розв'язано вірно, то цю конфетку кладуть у вазочку. Перевіривши вірність

4.     Гра «Збираємо грибочки у лісі».

Намальовано ліс і по два-три однакових грибочки (в залежності від кількості команд або учнів, що грають у цю гру). На однакових грибочках, записані паралельні завдання. Розв'язані грибочки - завдання відкладаємо окремо, а потім перевіряємо вірність виконання. Кращим грибником буде той, хто має більше грибочків, завдання яких вірно виконані.

Дані ігри можна використовувати в 5 -6 класах.

5.     Гра «Зоряне небо».

Цю гру можна використати у 5-9 класах. Грає дві або кілька команд. На однакових «зірках» записані паралельні завдання. Гра має кілька етапів. Кожен етап - мікроконкурс, який може містити матеріал одного вивченого параграфа. З тильної сторони «зірки» записане завдання, а з лицьової - номер етапу, щоб учні могли паралельно йти по вказаних етапах. В залежності від вірності І виконання завдання, вчитель дає команді «зірку» або ні. Приходячи до кінця гри, підраховуємо кількість зірок, що одержала кожна команда, і визначаємо переможців. Якщо команди одержали однакову кількість «зірок», то задаються додаткові питання, завдання.

6.     Гра «Йдемо по стежинці».

1)                       Наша стежинка біжить від курчатка, що радіє сонечку, до веселого зайчика з морквинкою, а потім приходимо по ній до річечки, де котик ловить рибку, синичка купається у калюжці коло стежинки. Наша стежинка приводить нас до їжачка, що п 'є молочко, а мишка мирно живе в своїй нірці.

2)                       Можна і подорожувати і по другій стежинці. Від жабки квакушки, що живе у очереті до метелика, що літає на лужку. У лісі ми зустрічаємось з ведмедиком, а на подвір'ї нас зустрічав півник та собачка. Грає дві команди або два учні, тому коло кожного звірятка два завдання, що записані на листочках різних кольорів. Такі стежинки можна подати у вигляді ламаної та використати при виконанні практичної роботи «Довжина ламаної» та інших.

7.    Гра «Кущик, що цвіте».

Намальовано квітучий кущик. На кожній квітці записано завдання. Цю гру краще використовувати при узагальненні і повторенні матеріалу. Квіти намальовано попарно однакових величин, або пронумеровані, а на кожній парі задано подібні завдання. Учні стають у два ланцюжки. Вони підходять до куща по черзі і вибирають квітку від меншої до більшої, від простішого завдання до складнішого. «Розв’язану» квітку передають наступному учаснику команди, який вибирає свою квітку і виконує завдання. До кінця ланцюжка команда повинна мати «букет» квітів. Потім команди міняються букетами і перевіряють вірність виконання завдань. Квіти, де невірно розв'язанні - завдання, відкладаємо в бік. Команда з

більшим «букетом» виграє.

8.    Гра «Математичний футбол».

Ця гра цікава для учнів від 5 до 9 класу. За кілька днів до уроку, на якому буде проходити гра, вчитель повідомляє її тему і форму завдань (питання, задачі, рівняння, рахунок), їх складають учні. Завдання повинні бути досить прості, щоб учень міг їх розв'язувати усно. Ділимо клас на дві команди.

Учень з однієї команди кидає м'ячик до іншої.

М'ячик можна вибирати довільний, краще тенісний. Учень, що зловив м'ячик, одержує завдання або питання і розв'язує його. За уміння скласти завдання або питання та уміння їх виконувати учням ставлять від одного до п 'яти балів. Якщо учень не може відповісти на питання, виконати завдання або його задати, команда одержує «гол» та втрачає один бал. Дана гра допоможе мобілізувати учнів на активну розумову діяльність, розвиватиме уміння швидко виправляти помилки, які допущені «футболістами» іншої команди поряд з цим, при складанні ними завдань, учні вчаться всебічно обдумувати і розглядати вивчений матеріал.

9.    Гра «Цікаві квадратики».

Вона допоможе учням навчатись знаходити закономірності та уміння використовувати їх. Задано квадратик і кілька чисел в ньому. Це можуть бути числа, що діляться на 5; 7; 10; 11 або для 9 класу члени арифметичної та геометричної прогресії.

Прикладом такого квадратика і комбінації чисел у ньому може бути:

Даний квадратик

	28
		35

 

Маємо одержати

21	35	28
35	28	21
28	21	35

Отже, потрібно, знайшовши особливості даних чисел, заповнити порожні клітинки квадратика. Для учнів буде цікавіше, коли вони самі складатимуть такі квадратики і задаватимуть їх класу.

Поряд з цим, весь урок можна присвятити грі, що зацікавить учнів.

1.      Під час екскурсії на природу учні навчаються виконувати вимірювання відстаней до недоступних предметів. Ці питання розглядаються в залежності від матеріалу, що вивчається в даному класі.

2.      Урок - інтерв’ю.

За кілька днів до уроку, вчитель виділяє тему і учні, узагальнюючи матеріал, працюють над нею. Кожен з них має скласти кілька питань або усних завдань. На даному уроці вибираємо «вченого», у якого «репортери» беруть інтерв'ю. В більшості таких запитань варто задавати не більше п'яти. Правильна відповідь дає «вченому» два бали, а невірна - збирає один бал. «Вченому», що дав змістовні і конкретні відповіді, можна дати два бали. Потім працюємо з наступним «вченим», який набрав найбільше балів.

В даній групі учні вчаться робити пояснення з вимогами стислості граматичної досконалості мови і оцінювання мови товаришів. Цю гру доцільно використовувати в 7-9 класах.

3.      Урок-захист дисертації.

Даний урок більш ширший, ніж попередній. Один учень готує дисертацію-реферат або готує усну доповідь по заданому питанню. Після цього рада, тобто учні класу, задають йому підготовлені наперед питання. Учні навчаються висловлювати свою думку, відстоювати її, та й написання реферату дає змогу взнати нове для учнів.

4.      Урок-конференція.

Конференція - збори, нарада представників держав або членів чи представників громад, наукових та інших організацій. На ній обговорюються і розв'язуються будь які питання. Учитель за кілька уроків наперед оголошує питання, по якому проходитиме конференція. Учні класу поділяються на «наукові організації», які працюють, використовуючи додаткову літературу, формують свою думку по даному питанню. На початку уроку вчитель оголошує тему і питання конференції. Учні кожної «організації» висловлюють свою думку. Враховується не тільки вірність відповіді, а й уміння відстояти і висловити свою думку. Так можна працювати у 7 - 9 класах.

Застосування інтерактивних форм та методів навчання на уроках математики і фізики дають змогу вчителю орієнтуватись на особистість учня як суб'єкта навчання, не привчати учня до «єдино правильних істин», до одноманітного бачення світу, а розвинути в дітей прагнення мислити під час розв'язання проблем, діяти.

 

 

Кожному вчителю потрібно пам'ятати вислів В.О. Сухомлинського:

«Не опікайте мене, не ходіть за мною, не зв’язуйте кожен мій крок, не сповивайте мене пелюшками нагляду і недовір'я, не нагадуйте й словом про мою колиску. Я - самостійна людина. Я не хочу, щоб мене вели за руку.

Переді мною висока гора. Це - мета мого життя. Я бачу її, думаю про неї, хочу досягти їі, але зійти на цю вершину хочу самостійно. Я вже піднімаюсь, роблю перші кроки, і чим вище ступає моя нога, чим ширший  круг відкривається переді мною, тим більше людей бачить мене. Від величі і безмежності того, що мені відкривається стає страшно. Мені потрібна підтримка старшого друга. Я досягну своєї вершини тоді, коли опиратимусь на плече сильної і мудрої людини. Але мені соромно і боязко сказати про це. Мені хочеться,щоб усі вважали, що я сам, самостійно, своїми силами доберусь до вершини».

У зв'язку з цим, мудрі слова: «Учень - не посудина, яку треба наповнити, а смолоскип, який треба запалити!» є актуальними в сучасних умовах роботи вчителя.

 

 

 

 

 

 

 

 

 

 

 

 

 

Тема уроку: Теорема Піфагора

 Мета уроку: Познайомити учнів зі змістом і доведенням теореми Піфагора та наслідків з неї; показати застосування теореми при розв’язуванні задач. Розвивати логічне мислення школярів, формувати навики самооцінки, виховувати інтерес до історії математики.

 Обладнання уроку: Комп’ютер, дошка, портрет Піфагора, плакати з усними вправами, малюнки до задач, картки для практичних робіт, математичне лото.

         Тип уроку: урок засвоєння знань та умінь.

         Очікувані результати: 

          засвоєння учнями теореми Піфагора і наслідки з неї;  вироблені уміння розв’язувати найпростіші задачі з теми;

 викликаний інтерес до біографії Піфагора як легенди і джерела дискусії;  вдосконалені навики роботи на комп’ютері, застосування їх для здобуття нових знань;  навчання учнями робити власні висновки.

 

План уроку І. Організаційний момент.

Вчитель: Світ, що нас оточує, - це світ геометрії. Тому запрошую вас до його пізнання і нехай сьогоднішній урок стане ще одним віконцем у дивовижний і цікавий математичний простір. Я надіюся на нашу співпрацю, свідоме засвоєння матеріалу уроку, зацікавленість до продовження роботи над колективним проектом.

Запишіть, будь-ласка, число, класна робота і свої очікування від уроку.

 У кулачному бою на  58-й Олімпіаді, яка проходила в 548 році до н.е. брав участь один із давньогрецьких математиків. Переказують, що через малий зріст судді не хотіли допустити його до змагань.

 - Можливо, - заперечив молодий вчений, - мій вигляд і не викликає у вас довір’я. Але я буду наносити удари з такою математичною точністю, що супротивникові стане жарко. Моя глибока віра в число – це моє життєве кредо.

          І він додержав свого слова – став чемпіоном з цього виду спорту і утримував цей титул ще на кількох олімпіадах.

 То ж нехай його слова: „ Тимчасова невдача краща від тимчасової удачі” стануть девізом уроку.

          ІІ. Актуалізація опорних знань та умінь.

1. Вправа „Мозковий штурм”:

-         Як називаються елементи прямокутного трикутника?

-         Що називається косинусом гострого кута прямокутного трикутника?

-         Чи може у прямокутному трикутнику бути тупий кут?

-         Дано кути, градусна міра яких різна. Які косинуси цих кутів за величиною?

-         Чи залежить косинус кута від розмірів трикутника? Від розміщення трикутника на площині.

2.     Усні вправи за плакатами:

Обчислити косинуси гострих кутів даних трикутників:

 

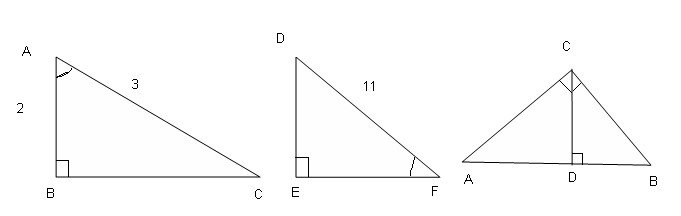
3.     Практична робота:

а) індивідуальні картки (2 чолов.);

          б) математичний диктант:

-   накресліть прямокутний трикутник із катетами 3 і 4 см;

-   виміряйте гіпотенузу;

-   знайдіть квадрати довжин усіх сторін;

-   знайдіть суму квадратів катетів;

-   порівняйте квадрат гіпотенузи із сумою квадратів катетів; - зробіть висновок.

          Вчитель. Що одержали учні, які працювали на картках? Як ви вважаєте: це  випадковість чи закономірність?

          ІІІ. Повідомлення теми, мети уроку, мотивація навчальної діяльності.

          ІV. Засвоєння нових знань.

1.     Формулювання теореми Піфагора.

Вчитель. А чи потрібна теорема Піфагора в житті? Побачимо.

2.     Усне розв’язування задач на знаходження гіпотенузи прямокутного трикутника (використовуються малюнки до задач) – „Займи позицію”.

А) Знайдіть довжину приставленої до будинку драбини, якщо нижній кінець знаходиться на відстані 3 м від будинку, а верхній – на стику стіни й даху.

Висота стіни будинку дорівнює 4 м.

          Дано: ∆ АВС, С = 90⁰, АС= 3 м, ВС= 4 м

          Знайти: АВ

Розв’язання

           АВ – гіпотенуза ∆ АВС. За теоремою Піфагора АВ² = АС² + ВС²; АВ² = 3² + 4²

= 9+ 16 = 25. АВ = 25 = 5 (м).

          Відповідь. 5 м.

 Б) Висота новорічної ялинки 6 м. Для закріплення її у вертикальному положенні від вершини ялинки зробили натяжки АВ, АВ₁, АВ₂ однакової довжини і закріпили їх на підлозі на відстані 4 м від основи ялинки. Якої довжини повинна бути натягуюча проволока, щоб ялинка стояла вертикально. 

 Вчитель. Теорема – це твердженнят яке доводять. Виділимо умову і висновок теореми Піфагора.

3.     Доведення теореми ( самостійне опрацювання матеріалів слайдів на комп’ютері).

 

 

        

                     

 

 

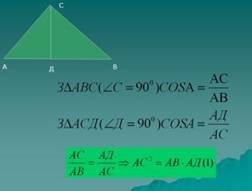
4.     Рівневі завдання (на комп’ютері).

                          

        

 

5.     Вправи для зняття втоми очей.

1.Швидко кліпати очима протягом 15 с.

2.Заплющити очі. Не відкриваючи очей, начебто подивитися ліворуч на рахунок „раз-чотири”, повернутися у вихідне положення. Так само подивитися праворуч на рахунок „п’ять-вісім” і повернутися у вихідне положення. Повторити 5 разів.

3.Спокійно посидіти із закритими очима, розслабившись протягом 5 с.

6.     Історична довідка про Піфагора.

                       Вчитель.

Піфагор – один із найбільш знаменитих учених за всю історію людства. Він був не лише вченим і засновником першої наукової школи. Ця унікальна людина була і засновником першої наукової школи. Ця унікальна людина була і „володарем душ”, і проповідником власної „піфагорської” етики, і великим філософом. Піфагор виховав у людства віру в могутність розуму, переконаність у можливості пізнання природи, впевненість у тому, що ключем до таємниці світопобудови є математика.

                                 Учень робить повідомлення про Піфагора.

7.     Перевірка виконання рівневих завдань. Запис на дошці і в зошитах результатів.

с² = а² + в²,                             с = _{а в}                                     а² = с²- в²,                               а = с _в                                      в²= с² – а²,                              в = с _в

Наслідки теореми Піфагора: 

 

1.     а < с, в < c

2.     0 < cos α < 1

V. Формування практичних умінь 

 1. № 2 (3)

 У прямокутному трикутнику дано катети а і в. Знайдіть гіпотенузу,  якщо  а =4, в = 5.

       

 

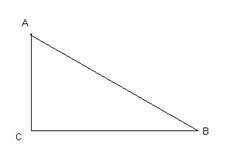
2.№ 3 (2)

    У       прямокутному     трикутнику          дано гіпотенузу с і катет а. Знайдіть другий катет,

якщо с = 10, а =4.

 

                       3.Сторони прямокутника 6 см і 10 см. Знайдіть його діагональ.

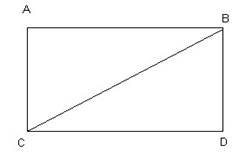
4.

                        Знайдіть сторону ромба, якщо його діагоналі дорівнюють 6 см і 8 см.

 

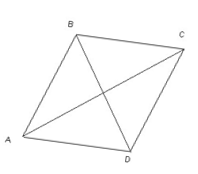
5. Вправа „Оціни себе”.

                       Середній рівень – математичне лото.

                        Достатній і високий рівні – тести.

VІ. Домашнє завдання

                       Додаткова задача (за бажанням учнів)

 На березі річки росла тополя висотою 11м. Буря зламала дерево на висоті 6 м від землі так, що вершина уперлась в інший берег. Знайдіть ширину річки СВ, якщо вважати, що_ АСВ = 90⁰.

    

         VІІ. Підсумки уроку.

1.     Усна вправа – знайдіть помилку – „Метод ПРЕС”.

 

 

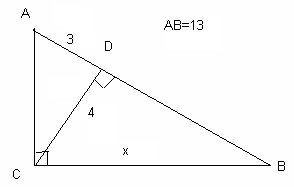
З ∆ DСА:  DА = 13-3 = 10,

                  Х² = 4² + 10² = 116

З  ∆ АВС:  ВС² = 16 + 9 = 25

                   Х² = 169 – 25 = 144

                   116 ≠ 144   

Вчитель. Історія теореми Піфагора цікава. Адже була відома у Вавілоні ще за 1500 років до народження Піфагора. Можливо, що тоді ще не знали її доведення, а співвідношення між гіпотенузою і катетами було встановлено дослідним шляхом на основі вимірів. Піфагор, очевидно, знайшов доведення цього співвідношення. Збереглася давня легенда, що на честь такого відкриття Піфагор приніс у жертву сто биків, хоча за іншими версіями вчений був непримиренним противником жертвування тварин, особливо великої рогатої худоби.

 В різних джерелах теорему Піфагора називають „теорема нареченої”, „ослиний міст”, „Піфагорові штани”.     

2.     Вправа „Мікрофон”. 

Що нового  дізнались на уроці?

Як читається теорема Піфагора?

Які наслідки з теореми Піфагора?

Що корисного для себе ви винесли з уроку?

Де, у яких ситуаціях ви можете використати набутий на уроці досвід?

Що було потрібним на уроці? зайвим?

Що ви очікували від уроку? чи збулися ваші очікування?

        

 Вчитель. Математику та літературу іноді ставлять на протилежних полюсах людського знання. Проте мости між літературою й точними науками ніколи не розводилися, адже людський інтерес не можна відділити від емоцій, а „сухі” формули не ізольовані від гарячого „випромінювання” людських почуттів.

  Сонет відомого німецького поета ХІХ століття Адельберта фон Шаміссо є прикладом гармонійного поєднання поезії з геометрією. Як Істину відкрив – сіять їй вічно, Вона нам – найнадійніша опора:

Так в древній теоремі Піфагора

Й донині бездоганно все й логічно.

 

Основа лото

Як читається теорема Піфагора?	Знайдіть катет прямокутного трикутника, якщо його гіпотенуза дорівнює 6 м, а інший катет – 3 м?
Чи правильне твердження: для будь-якого гострого кута α   0<cosα<1?	а с Для пропорції  запишіть в а основну властивість.
Знайдіть гіпотенузу прямокутного трикутника, катети якого дорівнюють  3 м і 4 м.	Що називають косинусом гострого кута прямокутного трикутника?

 

Написи на зворотній стороні карток для відповідей

Математичне лото

Теорема Піфагора

Гіпотенуза

Катет

с² = а² + в²

Набір карток для відповідей

	Квадрат гіпотенузи прямокутного трикутника дорівнює сумі квадратів катетів
а2 = в с	Так
Відношення прилеглого катета до гіпотенузи

 

 

У прямокутному трикутнику будьякий з катетів менший за гіпотенузу
Ні	а с =в а
	Відношення гіпотенузи до прилеглого катета

 

Практична робота

 

1.        Виміряйте довжини всіх сторін.

2.        Обчисліть квадрати довжин сторін.

3.        Знайдіть суму квадратів катетів.

4.        Порівняйте знайдену суму із квадратом гіпотенузи.

5.        Висловіть своє припущення.

Практична робота

 

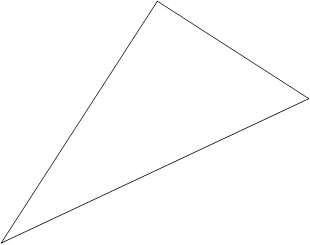1.Виміряйте довжини всіх сторін.

2.Обчисліть квадрати довжин сторін.

3.Знайдіть суму квадратів катетів.

4.Порівняйте знайдену суму із квадратом гіпотенузи.

5.Висловіть своє припущення.

 

Тести

 

1.   Як називаються сторони прямокутного трикутника, які утворюють гострий кут?

   а) катети     б) гіпотенуза        в) катет і гіпотенуза  г) два катети і

гіпотенуза

2.   Що називається косинусом гострого кута прямокутного трикутника?

                       а) відношення гіпотенузи до прилеглого катета

                        б) відношення прилеглого катета до гіпотенузи

                       в) відношення прилеглого катета до гіпотенузи

                       г) відношення прилеглого катета до протилежного

3.   Від чого залежить косинус гострого кута трикутника?

                       а) від розмірів трикутника

                       б) від градусної міри кута

                       в) від градусної міри кута і розміщення трикутника на площині

                       г) від градусної міри кута і розмірів трикутника

4.   Як читається теорема Піфагора?

  а) квадрат гіпотенузи прямокутного трикутника дорівнює сумі квадратів його катетів

                            б) квадрат гіпотенузи прямокутного трикутника дорівнює різниці

квадратів його катетів

                        в) гіпотенуза прямокутного трикутника дорівнює сумі катетів

                        г) с² = а² – в²

5.   Катети прямокутного трикутника дорівнюють 7 і 11 см. Чому дорівнює гіпотенуза трикутника?

              а) 15 см         б) 14 см         в) 13 см            г) інша відповідь

6.   Гіпотенуза прямокутного трикутника дорівнює 10 см, а один з катетів 8 см. Чому дорівнює другий катет?

              а) 2 см          б) 6 см            в)1 5 см             г) 10 см

7.   Порівняйте катети а і в прямокутного трикутника з його гіпотенузою.

                        а)  а < c, в > c

                        б)  a < c, в = c

                        в)  a > c, в > c

                        г)  a < c, в < c

8.   Що можна сказати про косинус гострого кута прямокутного трикутника?

                       а) cos α > 1     б) cos α = 0           в) cos α < 1        г) cos α = 1

 

Позакласний захід.

Тема: Інтелект-шоу "Еврика "

Мета: розширити і поглибити знання учнів з математики, виховувати культуру мовлення, розвивати інтерес до знань, логічне мислення, дисциплінованість, активність, самостійність, винахідливість, кмітливість.

Девіз: "Швидкість потрібна, а поквапливість шкідлива "

(О.Суворов)

Хід інтелект-шоу

Ведучий 1. У праці, навчанні, грі, в усякій творчій діяльності людині потрібні винахідливість, уміння міркувати - те, що називають "кмітливістю". Кмітливість можна розвивати, розв'язуючи творчі, логічні математичні задачі як зі шкільного курсу математики, так і задачі, які виникають з практики і пов'язані зі спостереженнями та речами, подіями в навколишньому світі.

Ведучий 2. Сьогодні ми з допомогою її величності Математики та нашого шановного журі визначимо найкмітливішого з кмітливих.

(Знайомство з учасниками гри і членами журі)

Ведучий 1. Для визначення послідовності участі в конкурсах проведемо відбірний тур.

Запитання відбірного туру

1.   Назвіть прізвище вченого який ввів новий метод математичних досліджень - метод координат?

(РенеДекарт)

2.   Хто з видатних математиків сказав: "Дайте мені точку опори, і я поверну Землю "?

(Архімед)

І. Конкурс "ТЕМА "

Теорема Піфагора

1.         Як називають сторону прямокутного трикутника, яка лежить проти прямого кута?

(Гіпотенуза)

2.         Як називають прямокутний трикутник зі сторонами 3, 4, 5 ?

(Єгипетський)

3.         Піфагор Самоський, Михайло Кравчук, Софія Ковалевська, Амедео Авогадро - відомі вчені. Хто з них не математик?

(Амадео Авогадро)

4.         Скільки можна провести висот у прямокутному трикутнику?

(Одну)

5.         Який математик був олімпійським чемпіоном з клубного бою?

(Піфагор)

6.         Яку теорему довів Піфагор?

(У прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів)

7.         Що коротше: катет чи гіпотенуза?

(Катет)

8.         Що називають, косинусом гострого кута прямокутного трикутника?

(Відношення прилеглого катета до гіпотенузи)

Чотирикутники

1.         Яку фігуру називають чотирикутником?

(Фігура, яка складається з чотирьох точок і чотирьох відрізків, що послідовно їх сполучають.)

2.         У якій трапеції можуть бути дві рівні сторони?

(У рівнобічної)

3.         Скільки діагоналей у паралелограма?

(Дві)

4.         Яка властивість протилежних сторін чотирикутника, якщо у нього можна вписати коло?

(Сума довжин протилежних сторін рівні)

5.         Якщо трапеція або ромб описані навколо кола, то їхні висоти дорівнюють...

(Діаметру кола)

6.         У якого чотирикутника діагоналі є бісектрисами його кутів?

(Уромба)

7.         Хто в перше довів рівність вертикальних кутів?

(Фалес)

8.         Чи можуть у паралелограма сусідні сторони бути рівними?

(Так, якщо він ромб)

Функції

1.           Що називають функцією?

(Відповідність, при якій кожному значенню змінної X з деякої множини О відповідає єдине значення змінної у)

2.           Яку функцію називають лінійною?

(Функцію виду у=кх+Ь)

3.           Що є графіком рівняння х²+у²=25

(Коло радіусом 5 і центром в початку координат)

4.           Скільки точок достатньо для побудови графіка Функції у=2005х?

(Дві)

5.           Хто перший ввів поняття змінної величини і систему координат?

(Р. Декарт)

6.           Яка область визначення функції у=2005х ?

(Множина всіх дійсних чисел крім числа 0)

7.           Яку функцію називають квадратичною?

(Функцію виду у=ах²+вх+с)

8.           Що є графіком оберненої пропорційності?

(Гіпербола)

II. Конкурс « ОРАТОР»

Ведучий 1: Геометрія - це наука про властивості геометричних фігур. Слово «геометрія» у перекладі на українську мову означає «землемірство». Така назва зумовлена застосуванням геометрії до вимірювань на місцевості.

Та чи потрібні у повсякденному житті знання геометрії?

Ведучий 2: Отже, тема конкурсу «Оратор» - «Чи вивчати геометрію?». Даємо одну хвилину на обдумування і одну хвилину кожному оратору промови.

ІП. Конкурс «ПОМІРКУЙ»

Ведучий 2. У цьому конкурсі учасники з трьох спроб повинні відгадати, про якого вченого йде мова.

Ведучий 1. Перша підказка. Свою діяльність він почав адвокатом. Він вів справи однієї дворянки і водночас навчав її єдину дочку Катерину астрономії. Навчаючи дівчину, він і сам захопився цією наукою. У нього виникає задум великої праці з астрономії. Щоб написати таку працю, потрібні були знання з тригонометрії, тому він сумлінно починає працювати над тригонометрію. Розповідають, що нерідко забувши навіть про їжу, він міг дві - три доби підряд просиджувати за своїм робочим столом, розв'язуючи якусь цікаву задачу або досліджуючи якесь складне питання. Головним результатом його роботи в галузі тригонометрії були вирази для синусів і косинусів кратних дуг.

Розповідають, що він швидко розв'язав задачу, запропоновану бельгійським математиком Ван Роменом як виклик математикам Європи.

Хто він?

Ведучий 2. Підказка друга.

Було це так. У жовтні 1594 р. Король ФранціїГенріх IV приймав нідерландського посла. Зайшла мова про видатних людей країни. Посол зауважив, що у Франції, мабуть, немає видатних математиків, бо мовляв, Ван Рооменне не назвав жодного француза. «Ви помиляєтесь, -відповів на це король. У мене є математик і досить видатний». І наказав покликати його.

Коли математик зайшов, посоли дав йому листа Роомена. Він прочитав його і тут же написав один з розв'язків рівняння, яке містилося у листі, наступного дня надіслав ще 22 розв 'язки, тобто знайшов усі додатні корені цього складного рівняння. Крім того, він виявив помилку в умові, що була допущена під час переписування, і виправив її. Хто він?

Ведучий 1. Підказка третя.

Задачею побудови на площині кола, що дотикається до трьох даних кіл, цікавилися ще давньогрецькі математики. Учений в одному з математичних творів опублікував спосіб розв 'язання цієї задачі за допомогою тільки циркуля та лінійки. Пишаючись знайденим розв’язкам, учений назвав себе «Аполлонієм галльським». Його вважають творцем алгебраїчних формул та алгебраїчної символіки, навіть називають «батьком алгебри». Хто це?

Ведучий 1. Йдеться про матемратика Франсуа Вієта.

IV.      Конкурс «ПІДКАЗКА»

Ведучий 2. У цьому конкурсі беруть участь гравці та їх асистенти. Асистент сідає обличчям до гравця. Позаду асистента демонструються малюнки, прилади тощо. Гравець за допомогою жестів, слів повинен пояснити те, що він бачить, так, щоб його помічник зумів розгадати картинку, прилад тощо.

Ведучий 1. Дійшла кінця перша частина інтелект - шоу «Еврика». Журі оголосить результати попередніх конкурсів, і один учасник який набрав найменше балів, залишить гру. Дякуємо йому за активну участь у конкурсах.

V.         Конкурс «ДУЕЛЬ»

Ведучий 2. Цей конкурс визначить переможця інтелект - шоу «Еврика». За правильну відповідь учасник отримує один бал.

1.   До яких чисел належить «чортова дюжина»?

(Простих)

2.   Чому дорівнює катет прямокутного трикутника, протилежний куту ЗО⁰?

(Половині гіпотенузи)

3.   Як трьома четвірками, не застосовуючи знаків, написати найбільше число?

(4⁴⁴)

4.   Хто вивів формули коренів квадратного рівняння ?

(Ф. Вієта)

5.   У лісі назбирали 5 склянок суниць. Суниці з 4 склянок переробили на варення. Скільки склянок залишилось?

(пять)

6.   Що ділить кут трикутника навпіл?

(Бісектриса)

7.   Хто з учених поділив числа на парні і непарні, прості та складені?

Він вважав, що «числа керують світом»?

(Піфагор)

8.   Як виразити число 10 п'ятьма дев'ятками?

9.   Якщо о 12-й годині йде дощ, то чи можна чекати, що через 72 години буде сонячна погода?

10.                       (Ні, бо буде ніч)

11.                       Проїхавши половину шляху, пасажир ліг

спати і спав доки не залишилось їхати половину того шляху, який він

проїхав, коли спав. Яку частину усього шляху він проїхав коли спав?

(шляху)

12.                       Який знак треба поставати між написаними поряд цифрами 4 і 5, щоб отримати число, яке більше за 4, але менше за 5?

(Кому, отримали 4,5)

13.                       За газету заплатили 1 грн. і ще половину вартості газети. Скільки коштує газета?

(2грн.)

13.3 одного гнізда вилетіло три ластівки. Коли вони будуть в одній площині?

(Завпеди)

14.                       Що важче: кілограм 25 - копійкових чи півкілограма 50 - копійкових монет?

(Кілограм 25 - копійкових).

15.                       У кошику лежить 7 яблук. Як поділити всі яблука між 7 дівчатками, щоб кожна одержала по одному яблуку і щоб одне яблуко залишилось у кошику?

(Дати шістьом дівчаткам по яблуку, а сьомій дівчинці - кошик зі яблуком, яке залишилось в ньому)

Ведучий 1. Голова журі підведе підсумок конкурсу і оголосить кінцеві результати.

 

Усний журнал

Життя видатних людей

Тема. Цікаві факти про Піфагора

 

Мета: збагатити і розширити знання учнів  про Піфагора, викликати інтерес до його яскравої особистості, його творів, думок, розвивати вміння  ораторського мистецтва, навички вільного володіння словом, формувати морально-етичні ідеали, розвивати творчість, виховувати впевненість у своїх силах, знаннях, самостійність, наполегливість у розв’язуванні задач, позитивне ставлення до навчання.

 

Обладнання: ілюстрації з зображенням Піфагора, пентаграми, персня піфагорійців, роздатковий матеріал до гри «Піфагорова головоломка», умова задачі Л.Пізанського для самостійного опрацювання (роздатковий матеріал).

 

 

 

 

 

Хід заходу

 

Учитель.

Найпопулярнішою з усіх теорем  планіметрії є теорема Піфагора. Причинами такої популярності є простота, краса і значення.  Про теорему Піфагора так сказав  німецький вчений Йоганн Кеплер: 

«У геометрії є два скарби: перший – теорема Піфагора, другий – золотий поділ. Перший можна порівняти з мірою золота, другий – із коштовним каменем».

Зі сторінок цього журналу ви дізнаєтеся про життя та досягнення людини, чиїм іменем названа ця теорема, а саме, про Піфагора, давньогрецького математика, філософа, засновника школи та напряму філософії, про інші аспекти його життя: про скромність у побуті, його погляди на мораль, про духовно-наукові дослідження, в яких до нього примкнули багато учнів.

                              

 

Методика проведення  заходу

Один за одним виходять учні зі сторінками в руках. У першого напис «Сьогодні у номері». 

Ведучий (оголошує): Усний журнал «Життя видатних людей», випуск перший: «Цікаві факти про Піфагора»

Кожний учень, який несе сторінку, повідомляє про те, що почують і побачать глядачі у журналі. Після чого ведучий запрошує до слова кожного виступаючого.

Ведучий: Ви дізнаєтеся про таке.

 

1   сторінка

Легенда про народження

                                   

Піфагор жив у 6 столітті до нашої ери. Він                                                        народився у Греції, на острові Самос у сім’ї                                золотих справ майстра Мнесарха. 

                              За  легендою оракул пророчив йому та його                                дружині Парфенісі народження сина, який                                буде славитися віками своєю мудрістю,                                справами та красою. Пророцтво збулося, і                                тоді Парфеніса приймає ім’я Піфіада, на                                честь   Аполлона   Піфійського,        а        сина називає Піфагором, на честь пророцтва Піфії. У легенді нічого не сказано про рік народження Піфагора, історичні дослідження датують його появу на світ приблизно 580 роком до нашої ери. 

2   сторінка

Дитячі та юнацькі роки

 

Можливості дати сину гарну освіту та виховання у Мнесарха були. Як і будь-який батько, Мнесарх мріяв, що син буде продовжувати його справу - ремесло золотих справ майстра. Життя вирішило інакше. Майбутній математик та філософ вже в дитинстві виявив велику здатність до наук. У свого першого вчителя Гермодамаса Піфагор отримав знання основ музики та живопису. Для покращення пам’яті Гермодамас примушував його вчити пісні з «Іліади» та «Одіссеї». Перший вчитель навчив Піфагора любити природу та вивчати її таємниці.

 Пройшло кілька років, і за порадою свого вчителя Піфагор вирішує продовжити навчання в Єгипті, у жерців. Потрапити до Єгипту у той час було дуже важко, тому що країну практично закрили для греків. За допомогою вчителя Піфагору вдається залишити острів Самос. Але до Єгипту далеко, і Піфагор поки що живе на острові Лесбос. Там відбувається знайомство Піфагора з філософом Ферекідом – другом Фалеса. У Ферекіда Піфагор навчається астрології, таємницям чисел, медицині та іншим обов’язковим, на той час, наукам.  Піфагор прожив на Лесбосі кілька років. Звідти шлях Піфагора лежить у Мілет до відомого Фалеса, засновника першої в історії філософської школи.

Навчання Піфагора в Єгипті сприяє тому, що він стає одним із найбільш освічених людей свого часу. Волею долі 12 років прожив Піфагор у Вавилоні, де прилучився до східної астрології та містики. І тільки в 60 років

Піфагору вдалося повернутися на Батьківщину.

 

Сторінка 3

Піфагорійська школа

 

Після повернення додому Піфагор  переселився   до Південної Італії, яку  тоді називали великою Грецією.  Тут, на острові  Сицилія в Кротоні, у нього  народжується власна філософська школа.

 

 

Це був одночасно і релігійний союз, і політичний клуб, і наукове товариство. Учні цієї школи зобов’язувались вести так званий піфагорійський спосіб життя. Статут піфагорійського союзу був дуже суворим. Кожний, хто вступав до нього, відмовлявся від особистої власності на користь союзу, зобов’язувався не проливати крові, не вживати м’ясної їжі, берегти таємницю вчення свого вчителя. Членам школи заборонялося навчати інших за винагороду. Всі учні Піфагора і він сам були працелюбні. Досконало володіючи методами єгипетських жерців, Піфагор «очищував душі своїх слухачів, виганяв вади з серця та наповнював уми світлою правдою». В «Золотих віршах» Піфагор показав ті моральні правила, суворе виконання яких призводить до ідеалу. Ось декілька з них: 

          Роби тільки те, що не засмутить тебе і не примусить розкаюватись.

                                                   Навчись тому, що слід знати.

                                                   Не нехтуй здоров’ям свого тіла.

                                                   Привчайся жити просто і без розкошів.

          Не закривай очей тоді, коли хочеш спати, не розібравши всіх своїх вчинків за минулий день.

 

 

                                     

На персні Піфагора було викарбувано такий девіз:  

«Тимчасова невдача краща                                        тимчасової удачі». 

 

У якості символа піфагорійці вибрали   пентаграму – п’ятикутну зірку.  Це символ здоров’я  і досконалості,  опізнавальний знак піфагорійців.

                                     

 

 

 

 

 

Сторінка 4

Філософське вчення Піфагора

 

Піфагор навчав медицині, принципам політичної діяльності, астрономії, математиці, музиці, етиці. З його школи вийшли відомі політичні та державні діячі, історики, математики та астрономи.

Це був не лише вчитель, але й дослідник.

Дослідниками ставали і його учні.

Піфагор розвивав теорію музики й акустики, створив відому «піфагорійську гаму». У школі Піфагора вперше був виказаний здогад щодо кулястості Землі.

 

Сторінка 5

Усе впорядковується відносно чисел

 

Піфагорійці вважали, що всі тіла складаються з найменших частинок, «одиниць буття», які в різних сполученнях відповідають різним геометричним фігурам. Число для Піфагора було і матерією, і формою всього світу. З цього уявлення виходила і основна теза піфагорійців: «Усе впорядковується відносно чисел». Тому пояснювати природні явища слідувало лише з їхньою допомогою.

Числам надавали містичних властивостей. Одні числа приносять добро, інші зло, успіх тощо. Піфагор вважав, що душа – теж число, вона безсмертна і передається від однієї людини до іншої. Числова містика Піфагора та його учнів нанесла великої шкоди розвитку математики. Сучасна церква признає числову містику. Так, у Біблії число 666 є число звіру, 12 несе щастя, а 13 – нещастя. Піфагор вважав, що число 5 символізує колір, 6 – холод, 7 – розум, здоров’я та світло, 8 – кохання та дружбу, 9 – постійність. Особливо ненависними піфагорійцям були числа 13 та 17.

 

Сторінка 6

Чи знаєте Ви, що…

 

…У Франції та Німеччині в епоху середньовіччя теорему Піфагора називали «ослячим мостом»? 

Учнів, що запам’ятовували теорему без розуміння, називали віслюками, оскільки вони не могли перейти через міст – теорему Піфагора.

 

…У математиків арабського Сходу ця теорема отримала назву «теореми нареченої»? 

Справа в тому, що в деяких списках «Начал» Евкліда ця теорема називалась «теоремою німфи» за схожість креслення з бджілкою, метеликом, що грецькою називалося «німфа». Але цим словом греки називали богинь, а також молодих жінок і наречених. Перекладаючи з грецької, арабський перекладач, не звернувши уваги на креслення, переклав слово «німфа» як «наречена», а не «метелик». Так з’явилася лагідна назва відомої теореми –

«теорема нареченої».

 

… Довівши свою знамениту теорему, Піфагор віддячив богам, принісши їм у жертву 100 биків? 

Це оповідання, найшвидше, вигадка, бо відомо, що Піфагор був вегетаріанцем і непримиренним противником забою та пролиття крові тварин. 

 

…Піфагор був переможцем на 58-х Олімпійських іграх, які проходили в 548 році до нашої ери, а потім перемагав ще на декількох Олімпіадах?

Відомо, що Піфагор  був міцним юнаком з товстою  шиєю та коротким носом,  малим на зріст, тому судді однієї  з перших олімпіад не хотіли  допускати його до змагань.  Але він пробився і «побився»  зі своїм супротивником та ще і 

переміг. Якби це трапилося якихось 2540 років вперед, газети всього світу вийшли б з аншлагом: «Нікому не відомий Піфагор завоював золоту медаль у кулачному бою». Ось чому серед знаменитих олімпійських чемпіонів він довго залишиться найвідомішим. Ось чому люди пам’ятають його більше, як дві з половиною тисячі років, тому що йому випало щастя перемогти не тільки супротивників, а й перемогти час.

… Іменем Піфагора названо кратер на видимій стороні Місяця.

 

Сторінка 7

Гра «Піфагорова головоломка».

                                                   

Це головоломка і конструктор одночасно. З її елементів можна       створювати силуети різних                                                    предметів і геометричних фігур складної конфігурації. 

Стародавня гра сприяє розвитку                                                     інтелекту.  

 

 

 

Сторінка 8

Поетична сторінка

 Життя – театр, а всі ми в нім актори,

Ми знаємо багато різних див,  Та пам’ятати будем Піфагора, 

Що теорему «золоту» створив.

 

 Вивчай в житті ще й інші теореми,

Щоб звався ти ученим джентльменом,

То й з розумом не матимеш проблеми

І виростеш культурним бізнесменом.

 

Сьогодні все. Вам, друзі , на прощання

Рекомендовано домашнєє завдання,

Над геометрією хай ніхто не плаче, А краще хай розв’язує задачі.

Сторінка 9

Старовинні задачі

Серед старовинних задач є задача Л.Пізанського (ХІІ-ХІІІ ст.), яка розв’язується за допомогою теореми Піфагора.

Дві вежі, одна з яких заввишки 40 футів, а друга – 30 футів, розташовані на відстані 50 футів одна від одної. До криниці, що знаходиться між ними, одночасно з обох веж злетіли по пташці. Рухаючись з однаковою швидкістю, вони прилетіли до криниці одночасно. Знайти відстань від криниці до найближчої вежі (у футах).

У кінці журналу учні зі своїми сторінками виходять на сцену і говорять: «Наш випуск закінчений. Все, що ви хотіли б побачити, повідомте редакції усного журналу в своїх листах у вигляді пропозицій та побажань».

Урок з фізики  

Тема. Електричне поле. Взаємодія заряджених тіл. Закон Кулона.

Мета. Навчальна: роз’яснити учням фізичний зміст закону Кулона й указати         межі його застосування.       Розкрити    матеріальний   характер електричного поля. 

 Виховна: виховувати  культуру поведінки, світогляд, позитивні людські якості.

 Розвивальна:         розвивати   вміння        аналізувати,   узагальнювати, формувати вміння розв’язувати задачі на закон Кулона.

Тип уроку: урок вивчення нового матеріалу.

                          Наочність:    навчальна    презентація    по    темі    «Електричне    поле.

Взаємодія заряджених тіл. Закон Кулона.»

Хід уроку І. Організаційний момент.

а) Привітання

б)  Перевірка готовності учнів до уроку.

в) Оголошення теми і мети уроку. Слайд № 1                                        

Слайд № 2 ІІ. Перевірка домашнього завдання. 

ІІІ. Актуалізацію опорних знань проводжу у формі бесіди.

1)  Електричний заряд – це…

2)  Скільки родів заряду існує у природі?

3)  Як поводять себе різнойменні, однойменні заряди?

4)  Коротко опишіть будову атома.

5)  Чому модель будови атома називають планетарною?

Слайд № 3 Слайд № 4

Слайд № 5

ІV. Мотивація навчальної діяльності учнів. Проводжу використовуючи навчальну презентацію.

                                             Слайд № 6                               

V. Вивчення нового матеріалу.

5.1. Попередні міркування

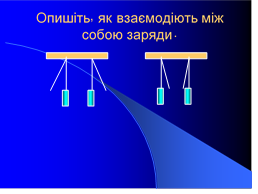
 Сила взаємодії зарядів залежить від самих зарядів та відстані між ними. Шарль Кулон дослідив за допомогою крутильних терезів зарядженість бузинових кульок, які вважали точковими зарядженими тілами. 

 Точковий заряд – електрично заряджене тіло, розмірами якого можна знехтувати порівняно з відстанями від нього до інших заряджених тіл, що розглядаються.

  Ми з вами бачили на досліді, що заряджені тіла взаємодіють між собою, тобто притягуються або відштовхуються. Причому ця взаємодія може відбуватися на відстані – за відсутності безпосереднього «контакту» між тілами.

Як передається дія одного тіла на інше? Можна припустити, що через повітря. Але якщо повторити досліди в безповітряному просторі, то взаємодія не зникне!. Відповідь на це питання було надано у роботах англійських учених 19 ст. Майкла Фарадея та Джеймса Максвелла.

Слайд № 7 Слайд № 8

 Відповідно до їх теорії простір навколо тіла, яке має електричний заряд, відрізняється від простору, навколо не наелектризованого тіла. Електричний заряд оточений електричним полем. 

 Електричне поле - особлива форма матерії, що існує навколо заряджених тіл, і через яку відбуваються електричні взаємодії.

 Електричне поле діє лише на заряджені частинки. 

 5.2. Дослід Кулона 

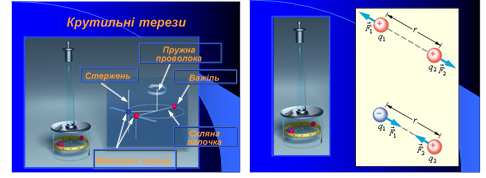
Електрометр є досить грубим приладом; він не дозволяє досліджувати сили взаємодії зарядів. Уперше закон взаємодії нерухомих зарядів був встановлений французьким фізиком Ш. Кулоном (1785р.).У своїх дослідах він виміряв сили притягування й відштовхування заряджених кульок за допомогою сконструйованого ним приладу – крутильних терезів, що вирізнялися високою чутливістю Будова крутильних терезів.

        Слайд № 9                                              Слайд № 10

              Слайд № 11                                   Слайд № 12

 Ідея вимірів ґрунтувалася про те, що якщо заряджену кульку привести в контакт із точно такою незарядженою, то заряд першої розділиться між ними нарівно. Таким чином зі зменшенням відстані у 2 рази, призвело до збільшення сили взаємодії у 4 рази.

 5.3. Закон Кулона.

 У результаті багатьох дослідів Кулон встановив закон взаємодії електричних зарядів.

Слайд № 13                                             Слайд № 14

 Закон Кулона.

Сили взаємодії двох нерухомих точкових зарядів прямо пропорційна добутку модулів цих зарядів і обернено пропорційна квадрату відстані між ними.

q1  q2

F _ k R₂

 – коефіцієнт пропорційності, який дорівнює k  9 10    9 Н м            ² . к

Кл

Слайд № 15

    6. Узагальнення вивченого матеріалу. Проводжу закріплення матеріалу розв’язуванням задач.

Слайд № 16                                  Слайд № 17 Задача 1. 

З якою силою взаємодіють два точкових заряди до 10 нКл розташовані на відстані 3 см один від одного.

Розв’язання:

F - ?	=10-9Кл =10-9Кл =0,03м	q F  k 1 2q2 R	Н м Кл Кл 2          F       2       2                                      Кл          м                                     9 1018           105              F  910  2  0,03
q1 = 1 нКл q2 = 1 нКл R = 3  см

Н

(Í )

k= Н м 2 2 Кл

9∙109

 Відповідь: 10^-5 Н.

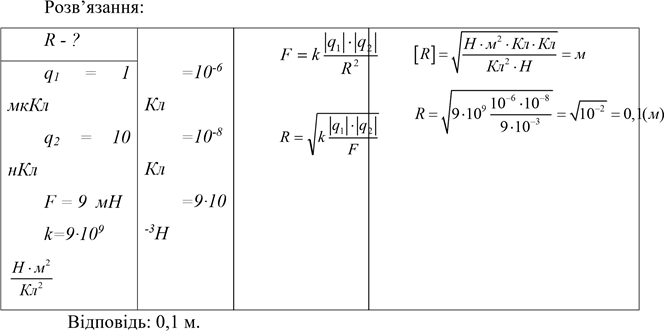
 Задача 2. 

На якій відстані один від одного заряди 1 мкКл і 10 нКл взаємодіють із силою 9мН.

VII.      Підсумок уроку.

Слайд № 18

VIII.   Домашнє завдання.

                             

Взаємодія заряджених тіл. Закон Кулона.

Мета уроку: 

Освітня:

•      сформувати знання учнів про точкові заряді, про силу взаємодії між зарядами;

•      пояснити взаємодію заряджених тіл існуванням електричного поля навколо них;

•      ознайомити з впливом електричного поля на живі організми; 

•      довести до розуміння учнів один з основних законів електростатики - законом Кулона; 

•      роз'яснити фізичний зміст закону Кулона та  вказати межі його застосування;

•      формувати вміння застосовувати закон при розв’язку якісних та обчислювальних задач;

•      формувати науковий світогляд учнів;

•      продовжити роботу з формування умінь працювати з текстом підручника.

Розвивальна:

•      сприяти оволодінню основними способами розумової діяльності, реалізації можливості розвитку мовлення в учнів;

•      вчити розкривати причинно - наслідкові зв'язки, узагальнювати та систематизувати знання;  вміти включити нові знання в систему раніше вивчених;

•      вчити розуміти запропоновану проблемну ситуацію та провести аргументоване судження;

•      розвивати в учнів уміння спостерігати, аналізувати, висувати гіпотези, припущення, будувати прогнози, узагальнювати, порівнювати пізнавальні об'єкти, робити висновки, здійснювати самоконтроль, самооцінку і самокорекцію навчальної діяльності.

Виховна:

•      пробудити пізнавальний інтерес до предмета і оточуючим явищам; 

•      формувати вміння критично, але об'єктивно оцінювати явища;

•      виховувати в учнів відповідальність, працьовитість;

•      сприяти        розвитку     особистості          (уважність, спостережливість          та творчість);

•      виховувати почуття  моральної відповідальності за історичну спадщину вчених – фізиків.

Тип уроку: комбінований. 

Обладнання та засоби забезпечення навчального процесу: комп'ютер, мультимедійний проектор, екран, відеофільм "Шарль Огюстен Кулон"; бланк картки «Моя робота на уроці» (у кожного учня).        Хід уроку

(Слайд 1)      Епіграф до уроку: 

Радість бачити і розуміти –

є найпрекрасніший дар природи.

А. Ейнштейн.

            

1.     Організаційний момент 

Вчитель. Кожний з вас отримав картку «Моя робота на уроці» . Протягом  уроку ви повинні працювати з нею  та виставляти кількість набраних балів в  відповідну строку, що відповідає етапу уроку.

2.     Перевірка виконання учнями домашнього завдання практичного характеру. 

1   учень. Розв’язує біля дошки  задачу № 2.30 (Фізика. 9 клас: Збірник задач /

І. Ю. Ненашев)

Вчитель. Ми постійно перебуваємо в неосяжному океані електричних зарядів - природних і штучних, створюваних численними машинами, верстатами і самою людиною. А як же впливають електричні поля на  живі організми. Це було вашим домашнім завданням.   

2   учень. (Слайд 2)      Про вплив електричних полів на живі організми.

(презентація)  

Вчитель. На попередніх уроках ми з вами розглядали початки електростатики, її якісні закони (особливості). Починаючи з цього уроку, ми починаємо вивчати кількісні закони електромагнітних взаємодій, а сьогодні розглянемо основний закон електростатики - закон взаємодії двох нерухомих точкових заряджених тіл або часток (закон Кулона).  

- Але спочатку, давайте згадаємо, що ми з вами вивчили на попередніх уроках. (Слайд 3)       

3. Актуалізація опорних знань, навичок та вмінь.

1.   Тест

1 варіант 1.                 Сили, що діють на заряди, правильно вказані на малюнку малюнок         А                                 A.   тільки А B.    тільки Б C.    тільки В D.   Б і В E.    А і В 2.                 Якщо дві заряджені матеріальні точки притягуються, то обов'язково A. обидві мають позитивний заряд B.                обидві мають негативний заряд C.                одна має позитивний заряд, а інша - негативний D.               або обидві мають позитивний заряд, або обидві мають негативний заряд 3. Якщо дві заряджені матеріальні точки відштовхуються, то обов'язково A. обидві мають позитивний заряд B.                обидві мають негативний заряд C.                або обидві мають позитивний заряд, або обидві мають негативний заряд D.               одна має позитивний заряд, а інша – негативний 4. Одиниця виміру електричного заряду

2 варіант 1.                 В якому випадку взаємодію зарядів вказано правильно?   A.   тільки А B.    тільки Б C.    тільки В D.   Б і В E.    А і В 2.                 Відомо, що натиранням об хутро заряджаються палички з гуми, сірки, ебоніту, пластмаси, капрону. Чи заряджається при цьому хутро? A.               Так, тому що в електризації тертям завжди беруть участь два тіла і при цьому електризуються обидва; B.                Хоча в електризації тертям беруть участь два тіла, в дослідах завжди використовуються тільки палички. Тому можна вважати, що заряджаються тільки палички. 3. Як взаємодіють одна з одною

(в СІ)        А. Вольт        В. Ватт        С. Кулон D.   Ом E.    Ампер 5.                 Водяна крапля з електричним зарядом +2.10-8 Кл з'єдналася з іншого краплею, що володіє зарядом +2.10-8 Кл. Заряд утворилася краплі дорівнює A.          +4.10-8 Кл B.          +2.10-8 Кл C.          0 D.          -2.10-8 Кл E.           -4.10-8 Кл 6.                 Від водяної краплі, що володіє електричним зарядом +2 е, відокремилася маленька крапля з зарядом-3e. Електричний заряд частини, що залишився на краплі дорівнює A.          –5е B.          –3е C.          –е D.          +3е E.           +5е

ебонітова   паличка, наелектризована           тертям       об хутро,    і         скляна           паличка, наелектризована   тертям           об шовк? A.   будуть притягуватися B.    будуть відштовхуватися C.    не будуть взаємодіяти 4.                 Нейтральна        крапля розділилася           на      дві.    Перша володіє електричним зарядом + q. Яким зарядом володіє друга крапля? A.   +2q    B.    -q C.    +q    5.                 Чи можна створити або знищити електричний заряд? A.         Не     можна           створити     або знищити електричний заряд. B.                Створити можна, знищити не можна. C.                Створити не можна, знищити можна. 6.       Алгебраїчна       сума електричних зарядів атома в нормальному стані дорівнює нулю, тому він: A.заряджений негативно B.   електрично нейтральний C.   заряджений позитивно

 

Вчитель. А тепер самі перевірте чи виконали ви його правильно. За кожну правильну відповідь – 1 бал.

(Слайд 4)  Відповіді:

1   варіант: 1.В; 2.С; 3.С; 4.С; 5.А; 6.Е

2   варіант: 1.С; 2.А; 3.А; 4.С; 5.В; 6.В.

Заповніть картку «Моя робота на уроці» . Виставіть кількість набраних балів в строку – тест.

2.   (Слайд 5) А зараз я пропоную вам відгадати кросворд. (Слайд 6)     

1.   Як називається явище розділення електричного заряду?

(електризація)

Що отримують тіла в результаті електризації? (електричний заряд)

Яким символом позначається заряд? (q)

2.   За допомогою якої математичної дії виражений закон збереження електричного заряду? (сума, q1 + q2 + ..... + qn = const)

3.   Як називається величина, що характеризує дію одного тіла на інше? (Сила). Яким символом позначається сила? У чому вона вимірюється? Як зобразити силу?

4.   Як називається дія тіл один на одного? (взаємодія)

Як називається взаємодія між зарядженими тілами? (електромагнітна) 5. Як називається залежність, в якій при зменшенні однієї величини, інша збільшується? (обернена пропорційність)

Наведіть приклади оберненої пропорційності. Що таке пряма пропорційність? Наведіть приклади.

6. Як називається одиниця вимірювання електричного заряду?

 

4.                     Мотивація учбової діяльності школярів, повідомлення теми, мети і задач урока.

Діти, що ви знаєте про Кулона?

Сьогодні на уроці ми з вами познайомимося з основним законом електростатики - законом Кулона.

Запишіть у зошит (Слайд 7)  тему уроку «Взаємодія заряджених тіл. Закон Кулона».

Мета нашого уроку: (Слайд 8)   

•      вивчити поняття точкові заряди та силу взаємодії між зарядами;

•      пояснити взаємодію заряджених тіл існуванням електричного поля навколо них;

•      ознайомитися з впливом електричного поля на живі організми 

•      сформулювати один з основних законів електростатики - закон Кулона; 

•      пояснити фізичний зміст закону Кулона та  вказати межі його застосування;

•      навчитися    застосовувати      закон          при    розв’язку    якісних та обчислювальних задач.

5.                     Сприйняття та усвідомлення учнями нового учбового матеріалу. Вчитель. Перші кількісні результати по вимірюванню сили взаємодії двох точкових зарядів були отримані в 1785 році (Слайд 9)  французьким ученим Шарлем Огюстеном Кулоном.

-   Закон Кулона справедливий тільки для таких заряджених тіл, розміри яких малі порівняно з відстанню між ними. Такі тіла називаються точковими зарядами.

Запишіть визначення в зошит. (Слайд 10)   

Точковий заряд - заряд, зосереджений на тілі, розміри якого малі в порівнянні з відстанню до інших заряджених тіл, з якими він взаємодіє.

Поняття точкового заряду, як і матеріальної точки є фізичною абстракцією.

(Слайд 11)  Відеодемонстрація «Вчений Шарль Огюстен Кулон.»

-   Після перегляду фільму проаналізуємо відповіді на наступні питання:

Вчитель. (Слайд 12)  

1)  З яких елементів складаються крутильні ваги?

2)  Як Кулон визначив силу взаємодії заряджених сфер?

3)  В результаті численних вимірів сили взаємодії двох нерухомих точкових зарядів у вакуумі Кулон встановив залежність. Яку?

(Слайд 13)  Крутильні ваги:

1.   Незаряджена сфера

2.   Нерухома заряджена сфера 

3.   Легкий ізолюючий стрижень

4.   Пружна нитка

5.   Паперовий диск

6.   Шкала

 

мал. 1

Отже, Кулон визначав силу взаємодії заряджених куль по куту закручування нитки в залежності від відстані між ними.

- У результаті численних вимірів сили взаємодії двох нерухомих точкових зарядів у вакуумі Кулон встановив закон, названий згодом його ім'ям. (Слайд 14)  Закон Кулона: Сила взаємодії двох точкових нерухомих заряджених тіл у вакуумі прямо пропорційна добутку модулів зарядів і обернено пропорційна квадрату відстані між ними.

Діти, знайдіть визначення цього закону в підручнику на стор. 13 та запишіть собі в зошит. (Слайд 15)   

                ^{F k}         r2                   де:                                              

q ₁, q ₂ - величина зарядів [Кл]

У Міжнародній системі одиниць (СІ) за одиницю електричного заряду прийнято 1 кулон (1 Кл).

1 кулон - це точковий заряд, який діє у вакуумі на рівний йому точковий заряд, розташований на відстані, рівному 1 м, силою 9 • 10⁹ Н. r - відстань між зарядами [м]

Нм²

k - коефіцієнт пропорційності [Н • м²/Кл²] k=910⁹ _Кл2 

F- сила Кулона (кулонівська сила) [Н]

Вчитель. Прочитайте закон Кулона і формулу (по буквах і по назвах фізичних величин) - 2 учня.

(Слайд 16)  Дайте відповіді на питання:

1.   Як ви розумієте вислів «Сила прямо пропорційна добутку модулів зарядів»?

2.   Як ви розумієте вислів «Сила обернено пропорційна квадрату відстані між зарядами»?

3.   На якому малюнку заряди є точковими? Чому?

 

4.   У якому випадку виконується закон Кулона? Чому?

(Слайд 17)  Межі застосування закона Кулона. У формулюванні закону Кулона є вказівка на точковість зарядів. Розглянемо взаємодію двох металевих заряджених куль (мал. 2, а, б). Чи залежить сила взаємодії між кулями від знаку зарядів?

                                          

мал. 2

Учні. Згідно із законом Кулона модуль сили взаємодії між зарядами не залежить від знака заряду. 

Вчитель. Але в першому випадку заряди, взаємно притягуючись, розташовуються ближче один до одного, ніж у другому. З цієї причини сила взаємодії різнойменних зарядів виявиться більшою, ніж однойменних, тобто в даному випадку закон Кулона не застосовний, оскільки заряди куль не можна вважати точковими.

У формулюванні закону Кулона вказується на нерухомість взаємодіючих заряджених тіл. Річ у тому, що взаємодія зарядів здійснюється за допомогою електромагнітного поля, яке може розповсюджуватися і просторі з кінцевою швидкістю. Поняття часу в закон Кулона не входить, а входить тільки поняття відстані. Будь-яке зміщення одного із зарядів позначиться на іншому не відразу, а через деякий час, необхідний електромагнітному сигналу для того, щоб подолати відстань, яка розділяє заряди. Якби швидкість розповсюдження електромагнітного поля була б нескінченно великою, то закон Кулона був би справедливий як для нерухомих зарядів, так і для тих, що рухаються. Та оскільки електромагнітні сигнали розповсюджуються з великою, але кінцевою швидкістю, заряди, що рухаються, взаємодіють не так, як нерухомі.

      Якщо ж виконується умова v<<с , де v — відносна швидкість зарядів, а с — швидкість світла, то закон Кулона практично не зазнає істотних відхилень.

Отже, запишіть у зошит.

(Слайд 18)   Межі застосування закону:

-   Заряджені тіла повинні бути точковими.

-   Заряджені тіла повинні бути нерухомими, тому що при русі заряджених тіл проявляється дія магнітного поля, що виникає в результаті цього руху.

Фізкультхвилинка. (Слайд 19)   

6. Осмислення, узагальнення та систематизація знань.

Розв’язок задач

1. У скільки разів зміниться сила взаємодії між двома точковими зарядженими тілами, якщо:

а) відстань між ними збільшити в 3 рази;

б) заряд одного з них збільшити в 5 разів?

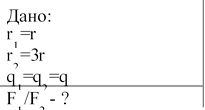 Розв’язання:

 

 9

 

5q²

 k r2

 5

 

(Слайд 20)  2.(Усно) Як зміниться сила кулонівської взаємодії, якщо ...

А) величина одного із зарядів збільшиться в 2 рази;

Б) величина одного із зарядів збільшиться в 3 рази, а другого зменшиться в 9 разів;

В) відстань між зарядами збільшиться в 6 разів;

Г) величина одного із зарядів збільшиться в 4 рази, а відстань між ними зменшиться в 2 рази;

(Слайд 21)  3. Визначте силу взаємодії двох однакових точкових зарядів по 1 мкКл, що знаходяться на відстані 30 см один від одного.

Розв’язання:

F  k qr1q2 ,q1  q2  F  k q22

                                                                                                                          2                                                      r

                                                                                                                            ⁹ (110^6)²        0,1(H)

                                                                                                 F  910      0,3₂                      

Н  м² Кл²

F      ₂     ₂  Н Кл      м

Відповідь: F=0,1 Н 

 

4.                     Сила взаємодії двох однакових точкових зарядів, що знаходяться на відстані 0,5 м, дорівнює 3,6 Н. Знайдіть величини цих зарядів.

 

 

 

5.                     На якій відстані потрібно розташувати два заряду 5 • 10 ^-9 Кл і 6 • 10 ^-9 Кл, щоб вони відштовхувалися один від одного з силою 12 • 10^-4 Н?

Дано:                       Розв’язання:

F=12•10^-4 Н k=9•10⁹ Н•м²/Кл² q₁=5•10 ^-9 Кл q₂ =6•10 ^-9 Кл r - ? 

 

(Слайд 22)  Задачі для самостійного розв’язку.

1.     № 3.5 (Фізика. 9 клас: Збірник задач / І. Ю. Ненашев)

Два позитивних заряди 1 і 2 нКл знаходяться на відстані 2 см один від одного. З якою силою вони відштовхуються один від одного? (Відповідь: 45 мкН.)

2.     Два однакові позитивні заряди перебувають на відстані 10 мм один від одного. Вони взаємодіють із силою 7,2 · 10^-4 Н. Визначте заряд кожної кульки. (Відповідь: 2,8 нКл.)

3.     Скільки електронів потрібно перенести з однієї порошинки на іншу, щоб сила кулонівської взаємодії між ними на відстані 1см дорівнювала 10 мкН? ( 2_10⁹ електронів)

4.     (високого рівня) № 3.18 (Фізика. 9 клас: Збірник задач / І. Ю. Ненашев) На вертикальну діелектричну спицю нанизують дві однаково заряджені кульки (мал. 3). Кульки можуть без тертя ковзати по спиці. На якій висоті над нижньою кулькою розташується верхня, якщо заряд кожної кульки становить

10 нКл, а маса 36 мг?

 

 

Мал. 3 

7. Підведення підсумків уроку. (Слайд 23)  

Оцінювання роботи учнів на уроці, аналіз досягнення мети і завдань уроку.

Вчитель. Заповніть картку «Моя робота на уроці».

Відзначте знаком «плюс» те, що ви добре зрозуміли на уроці і знаком «мінус» те, що зрозуміли погано або взагалі не зрозуміли.

1	Робота над тестом	Бали:
2	Кількість правильних відповідей на запитання вчителя	Бали:
3	Розв’язок задач	Бали:
4	Будова та принцип роботи крутильних терезів
5	Що таке пряма залежність між величинами
6	Що таке обернена пропорційність між величинами
7	Сенс закон Кулона
8	Як зобразити сили, що діють на заряджені частинки
9	Межі застосування закону Кулона
10	Як змінюється сила при зміні заряду
11	Як змінюється сила при зміні відстані між зарядами

 

Рефлексія (Слайд 24)   Оцініть свою роботу на уроці, склавши розповідь:

Сьогодні на уроці я працював (а)

__________________________________________________________________

Я зрозумів (а) (вкажіть номери зрозумілих питань):

__________________________________________________________________

У цьому мені допомогли:

__________________________________________________________________

__________________________________________________________________

Мені потрібно розібратися в таких питаннях (вкажіть номери незрозумілих питань): __________________________________________________________

Для цього потрібно:

__________________________________________________________________

 

У складанні розповіді вам можуть допомогти наступні слова.

 

Слова для оцінки роботи:

активно

пасивно

- прочитати записи по темі;

- прочитати інформацію з даної теми в підручнику;

- вивчити визначення, формулу, ...;

- навчитися зображувати сили;

- проконсультуватися з викладачем по питанню ...,

Вчитель. Хто бажає, прочитайте свої записи. (2 - 3 учні) Це і буде вашим домашнім завданням (кожному індивідуально).

8. Повідомлення домашнього завдання. 

 

 

 

 

Література

1.   Бевз Г.П. Алгебра. Підручник для 7 - 9 кл. серед, шк., - К.: Освіта, 2001

2.   ВінярЛ. Інновації на уроках/Математика в школах України: науково - методичний журнал. - 2006. - № 2.

3.   Віняр Л. Математичне доміно. Інтерактивні ігри для 6-11 класів//Математика в школах України: науково - методичний журнал. - 2006.

4.   Колеснікова Л. В., Коротуна Г. Й. Плани - конспекти уроків алгебри у 7 класі

5.   Погоріла Н. Урок алгебри у 7 класі з використання інтерактивних технологій навчання/Математика в школах України: науково - методичний журнал. - 2006. - №13

6.   Помету О., Пироженко Л. Сучасний урок. Інтерактивні технології навчання: Науково - методичний посібник. - К. :А. С. К., 2004

7.   Прохорова О. Впровадження сучасних педагогічних технологій в практику роботи/Математика в школах України: науково

- методичний журнал. - 2006. - №14

8.                  Сиротинко Г. Сучасний урок: інтерактивні технології навчання. -

X.: Видав. Гр. «Основа», 2003

9.                  Стиранка Н. Уроки алгебри у 7 класі. - Т.: Медобори, 2003

10.             Хроменко Н. Чотирикутники. Геометрія 8 кл. Технологія

«Акваріум»/Математика в школах України: науково - методичний журнал. - 2006. - №37

11.             Програма для загальноосвітніх закладів. Математика 5-11 класи.

12.             Інструктивна - методичний лист про вивчення математики у 2005 - 2006 навчальному році.

13.             Ю. Д. Кабалевська «Самостійна робота учнів в процесі навчання математики»

14.             В. П. Іржавцева. «Систематизація і узагальнення знань учнів у процесі вивчення математики».

15.             О.М. Осадча «Диференційоване навчання». «Математика в школах України» №9, 2002 р.

67

16.1. П. Жмур. «Активізація пізнавальної діяльності школярів».

«Математика» №14, квітень 2000р. 77. М Я. Крацький. «Методи та прийоми навчальної діяльності».

«Математика» №23 -24, 2001 р.

18. О. О.Агафонова. «Інтегровані форми та методи роботи на уроках математики». «Математика в школах України». №8 (926), березень 2005р. 19. Н. Ю. Харіна. «Інтерактивні методи роботи на уроках математики». «Математика в школах України». №6 (126), лютий 2006р.