Застосування методу координат до стереометричних задач

Застосування методу координат до стереометричних задач.

У курсі геометрії існують задачі, “класичне” розв’язання яких неочевидне, чи потребує великої кількості кроків, для розв’язання таких задач потрібно використовувати нестандартні методи, серед них метод координат. Метод координат часто є вигідним для певних класів задач, виділення ознак яких рідко зустрічається в літературі. Якщо при розв’язанні геометричної задачі або знаходженні геометричного місця точок (ГМТ), чи виведенні рівнянь прямих вводять координати точок, то зрозуміло, що використано метод координат.

Доцільність використання методу координат залежить від вдалого вибору координатних осей при розміщенні заданої фігури.

Розв’язують геометричні задачі координатним методом у три етапи:

1) записування задачі координатною мовою;

2) перетворення аналітичного виразу;

3) подання виразу за допомогою геометричних термінів, які входять до умови задачі.

Для розв’язування задач координатним методом важливо володіти вміннями:

1) виконувати побудову точки за координатами;

2) визначати координати заданих точок;

3) обчислювати:  відстань між точками; координати середини відрізка;

4) вдало вибирати систему координат;

5) складати рівняння фігури за її характеристичною властивістю;

7) бачити за рівнянням конкретний геометричний образ;

8) перетворювати алгебраїчні рівності. [1, с.233]

Проілюструю розв’язання задач координатним методом.

Задача 1.

У правильній чотирикутній піраміді із стороною основи 2 і висотою 4 знайти відстань від вершини кута основи до площини бічної грані, якій належить інша сторона основи.

Розв’язання:

Введемо прямокутну систему координат з початком в точці В,  основа ABCD правильної чотирикутної піраміди SABCD лежить в координатній площині XОY (AB OX; BCOY). Очевидно, що точки основи піраміди мають координати B(0;0;0); A(2;0;0); C(0,2,0); D(2;2;0). Оскільки S проектується паралельно OZ у центр квадрата основи, то її координати x i y дорівнюють координатам середин відрізків AB і BC відповідно  

Тоді вершина  піраміди буде мати координати: S(1;1;4).

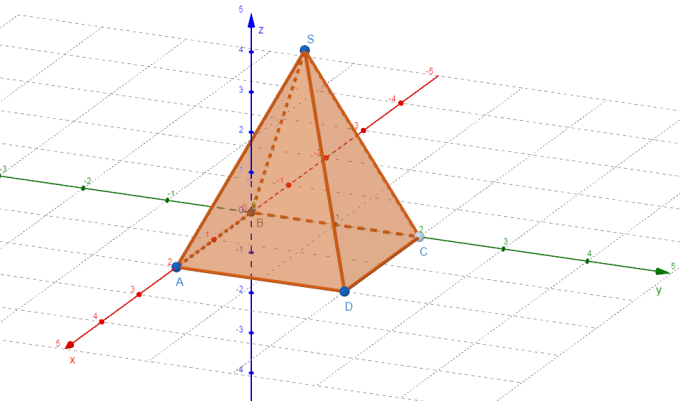Рис.1

За умовою потрібно знайти відстань від вершини кута основи B до площини бічної грані DCS, якій належить інша сторона основи.

Складемо рівняння площини DCS вигляду aх+bу+cz+d=0, де коефіцієнти a, b, c не перетворюються на нуль одночасно. Три точки D, C, S належать площині aх+bу+cz+d=0, отже їх координати задовольняють рівняння.

Маємо систему:

     

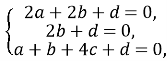
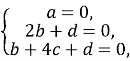
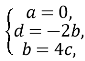
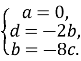
Нехай с=1. Тоді 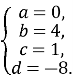  Рівняння площини DCS має вигляд: 4у+z-8=0

ρ = відстань від точки М () до площини ax + by + cz+d = 0.

Знайдемо відстань від точки B (0;0;0) до площини DCS.

. 

Відповідь: .

Задача 2.

Ребра AB, AD, і AA₁ прямокутного паралелепіпеда ABCDA₁B₁C₁D₁ відповідно дорівнюють 3 см, 1 см і 4 см. Знайдіть відстань від точки A₁ до площини BC₁D. [2, с.68]

Розв’язання:

Задамо прямокутну систему координат з початком в точці А,  нижня основа прямокутного паралелепіпеда ABCDA₁B₁C₁D₁ лежить в координатній площині XОY (ABOX; ADOY, AA₁OZ). Очевидно, що вершини прямокутного паралелепіпеда мають координати A(0;0;0); B(3;0;0); C(3,1,0); D(0;1;0); A₁(0;0;4); C₁(3;1;4).

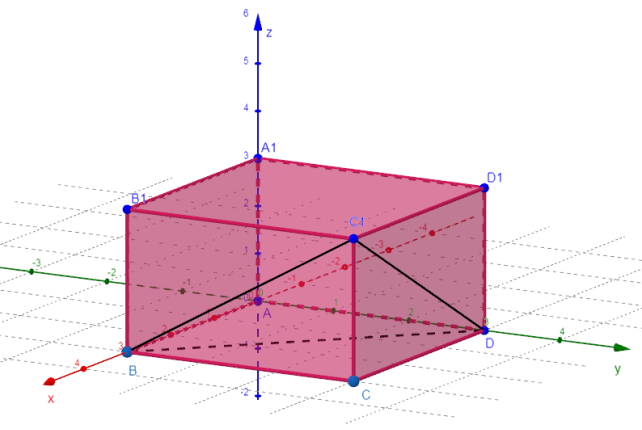Рис.2

За умовою потрібно знайти відстань від вершини A₁ до площини BC₁D. Складемо рівняння площини BC₁D. Нехай рівняння aх+bу+cz+d=0, задає площину BC₁D.

Маємо систему:

     

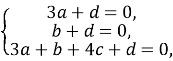
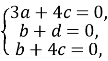
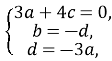
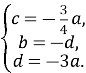
Нехай a=4 ( для зручності обчислення). Тоді 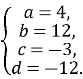  Рівняння площини BC₁D має вигляд: 4x + 12y - 3z -12 = 0

Знайдемо відстань від точки A₁ (0;0;4) до площини BC₁D.

. 

Відповідь:   см.

Задача 3.

Ребро куба має довжину 1. Знайдіть відстань між прямими, яким належать мимобіжні діагоналі двох суміжних граней куба. [3, с.54]

Розв’язання:

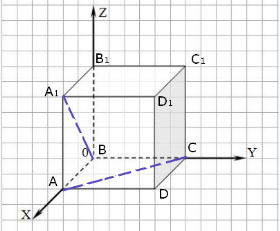Рис.3 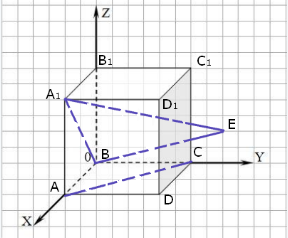Рис.4

Задамо прямокутну систему координат з початком в точці В,  нижня основа куба ABCDA₁B₁C₁D₁ лежить в координатній площині XОY (ABOX; BCOY, ВВ₁OZ). Очевидно, що вершини прямокутного паралелепіпеда мають координати А(1;0;0); B(0;0;0); C(0,1,0); A₁(1;0;1) (рис.3).

Знайдемо відстань між прямими A₁B і AC, яким належать мимобіжні діагоналі двох суміжних граней куба.

Відстань між мимобіжними прямими дорівнює відстані від довільної точки однієї з цих прямих AC, наприклад точки А до площини, що містить другу пряму A₁B й проведена паралельно прямій AC.

Проведемо через A₁B площину паралельно АС.  Для цього точку А паралельним перенесенням перенесемо у точку В, точку С у точку E на площині XOY (рис.4).



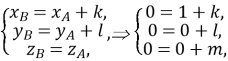
Тоді  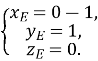 Таким чином, координати точки Е(-1;1;0).

Складемо рівняння площини A₁BE || AC. Відомо, що A₁(1;0;1), B(0;0;0); Е(-1;1;0).

Нехай рівняння aх+bу+cz+d=0, задає площину A₁BE.

Маємо систему:

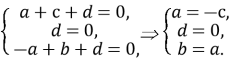
Нехай a=1. Тоді b=1, c= -1, d=0. Отже,  A₁BE задано рівнянням: x + y – z = 0.

Знайдемо відстань від точки А(1;0;0), до площини  x + y – z = 0.

.

Відповідь: .

Задачі на  координати включено до програми НМТ з математики, часто вміння використовувати знання про  координати дозволяє швидко розв’язувати складні завдання на НМТ.

Координатний метод дозволяє уникнути штучних побудов у геометричних задачах, спрощує розв’язування багатьох завдань. Учням, що мають достатній  і високий рівень знань подобається застосовувати традиційні знання у дещо незвичному форматі.

Література

1. Практикум з методики навчання математики. Основна школа: навчальний посібник для організації практичних занять і самостійної роботи  студентів  математичних  спеціальностей  педагогічних університетів  / за  редакцією  В. О. Швеця  -  К .:  Вид-во  НПУ ім. М. П. Драгоманова, 2012. - 267 с.

2. Мерзляк А. Г.,Полонський В.Б., Рабінович Ю.М., Якір М.С.  Геометрія 10 кл. профільний рівень: збірник задач і контрольних робіт. – Х.: Гімназія, 2018. – 112 с.

3. Апостолова Г.В. Геометрія 11 кл.: підруч. для загальноосвіт. навч.закл.: академ. рівень, профіл. рівень.- К.: Генеза, 2011.-304с.