Застосування похідної до дослідження функцій
Про матеріал
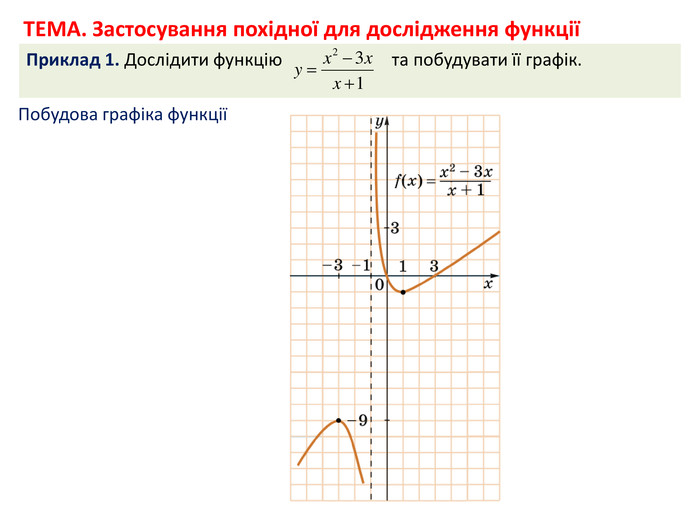
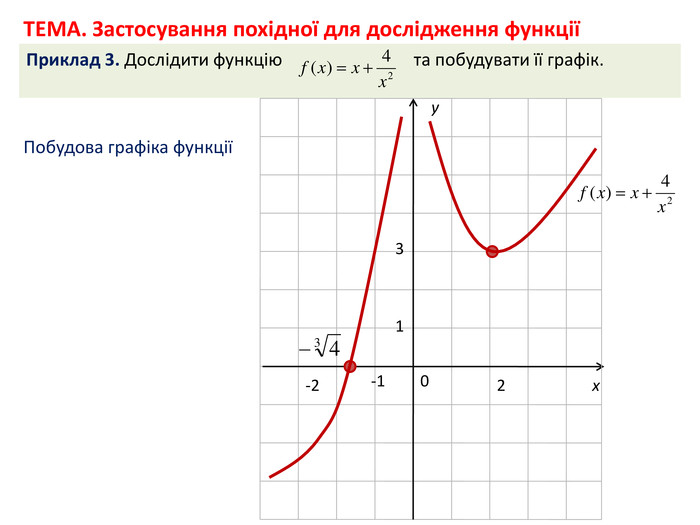
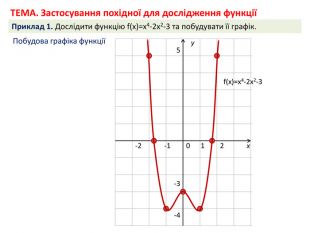
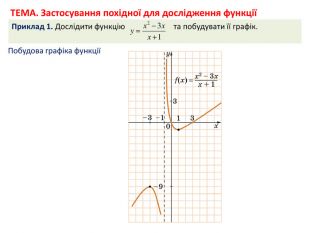
Презентація може бути використана вчителем при поясненні нової теми на уроці, а також учнями під час самостійного опрацювання нового матеріалу в умовах дистанційного навчання. Окрім пояснення нового матеріалу містить приклади розв'язування задач з даної теми з відповідними поясненнями. Перегляд файлу
Зміст слайдів
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку