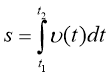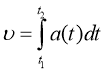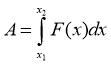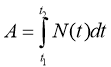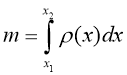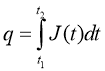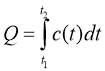Застосування похідної та інтеграла для розв’язування фізичних задач.

Інтегрований урок з фізики. Застосування похідної та інтеграла для розв’язування фізичних задач. 

Тема уроку: Застосування похідної та інтеграла для розв’язування фізичних задач.

Мета: навчальна: сформувати навички використання похідної й інтеграла під час розв’язування прикладних задач

розвивальна: закріпити та поглибити теоретичні знання з тем «Похідна “ , Інтеграл ; повторити певні теоретичні відомості з курсу фізики , необхідні для розв’язування  прикладних задач ; створити умови для формування навичок застосування похідної та інтеграла під час розв’язування фізичних задач;

виховна: виховувати почуття колективізму , товариської взаємодопомоги , культури міжособистісних стосунків під час групового розв’язування задач.

ОРГАНІЗАЦІЯ ТА ХІД УРОКУ

 I. Перевірка домашнього завдання

Матеріальна точка масою 2кг рухається уздовж осі ОХ за законом :

         X = 1/5t^{5 –} 1/4t⁴- 2/3t³ + 5.

Знайти :

а) початкову координату тіла ;

б) залежність проекції швидкості від часу ;

в) залежність проекції прискорення від часу ;

г ) залежність проекції рівнодійної сили на тіло від часу ;

д) залежність кінетичної енергії від часу ;

ж) побудуйте графік залежності проекції швидкості від часу й опишіть характер руху тіла на різних ділянках.

Очікувані відповіді:

а ) при t = 0   X = X₀ = 5 м;

б ) V_x(t) =t⁴ –t³ -2t² = t²(t²- t – 2 ) = t²(1+t)(t- 2)(м/с)

в) а_х(t)= 4t³ -3t²- 4t (м/с²);

г) R_x(t) = 8t³- 6t² -8t (H);

д) Е_к(t)= t⁴(1+t)²(t-2)²= t⁸- 3t⁷- 3t⁶+4t⁵+4t⁴(Дж);

e) V_x= 0 при t =-1c; t=0; t=2c;

ж) учитель математики перевіряє аналіз функції , її дослідження й побудову графіка в зошитах учнів. Далі графік для перевірки виводять на мультимедійну дошку , застосовуючи комп’ютерну презентацію. Учитель фізики описує характер руху тіла й показує відмінності « фізичного змісту» від «математичного».

Зміст основного матеріалу

 Учитель фізики згадує  вивчені раніше формули й ставить проблемні питання. У випадку нестаціонарного фізичного процесу на допомогу приходить математика:

 7 клас : формула густини m= p v, але буває p = p(v)

8 клас : формула розрахунку кількості теплоти    Q= C( t₂⁰-t₁⁰) , але

 C = C(t⁰)

7,9 клас: формула швидкості  V = S/t, найчастіше V =V(t)

7,9 клас: формула механічної роботи А = FS cos a , але буває F = F(s)

8,10клас: формула електричного заряду q =It, але найчастіше I =I(t)

Спільно учні й учителі фізики й математики заповнюють таблицю , що накреслена заздалегідь на дошці і супроводжують слайдом з презентації :

 

Величина	Співвідношення в диференціалах	Обчислення похідної	Обчислення інтегралів
m- маса p-густина	Dm=p(V)dV	p(V)= dm/dV
Q-кількість теплоти C-теплоємність	dQ=C(t0) dt0	C(t0)= dQ/dt0
A-механічна робота F-сила	dA=F(s)ds	F(s)= dA/ds
s-переміщення v-швидкість	ds=v(t)dt	v(t)=ds/dt
q-електричний заряд І-сила струму	dq=I(t)=dq/dt	I(t)=dq/dt

 Заповнений вигляд

Величини	Знаходження похідної	Знаходження інтеграла
s – переміщення, швидкість, А – прискорення	a(t) =
A - робота, F – сила, N - потужність	F(x) = A'(x) N(t) = A'(t)
m – маса тонкого стержня, - лінійна густина	(x) = m'(x)
q– електричний заряд, I –сила струму	I(t) = q(t)
Q – кількістьтеплоти с - теплоємність	c(t) = Q'(t)

 

Закріплення матеріалу

Фронтальне розв’язування задач :

Відомо ,що для будь-якої точки С неоднорідного стрижня АВ  об’ємом 0 ,2см³  , яка розташована праворуч від точки А , маса шматка стрижня АС у грамах визначається за формулою : m(V) =3V²+5V. Знайти густину стрижня : а) у середині відрізка АВ; б) наприкінці стрижня (точка В).

Нехай Q(t)-  кількість теплоти , яка  необхідна для нагрівання 1кг води від 0 до t⁰ (за цельсієм).

Відомо , що в діапазоні від 0 до 100 ⁰С формула : Q(t)= 4212t – 0,889t² + 6,58*10^-3t³ дає гарне наближення до експериментальної  залежності Q(t) . Знайдіть , як залежить теплоємність води від температури.

Матеріальна точка рухається прямолінійно за законом S_x = t³ -3t². Знайдіть швидкість і прискорення тіла в момент часу t =1с.

Робота автомобільного двигуна змінюється від переміщення за законом : A= 32S³+ 5S². Знайти силу тяги двигуна наприкінці другого метра шляху.

Кількість електрики , що протікає через провідник , починаючи з моменту t=0 для замкненого кола задається формулою : q =3t²+t+2. Знайдіть силу струму в момент часу t=3c.

 Розв’язування

 1. p(V) = m’ (V)= 6V +5

А) 6*0,1+5=5,6; b)6*0,2+5=6,2г/см³.

2.C(t⁰)=Q’(t⁰)= 4212- 1,778t⁰+1,974*10^-2t².

3.Vx(t)=S’_X(t)=3t²+ 6t ;  a_x(t)=6t+6;    V_x= 9м/с;   a_x =12м/с².

4.F(S)=A’(S) =96t²+10t;  F=40H.

5. I(t) =q’(t) =6t+1;     I=19A.

Рефлексія. Підбиваємо підсумок уроку  (Кінець першого уроку. Початок другого уроку.)

Організаційний момент

Зміст основного матеріалу

Знайомство з оберненою задачею. Неминучість застосування інтеграла , первісної. Учитель математики розповідає про використання невизначеного інтеграла, а вчитель фізики  - про визначений інтеграл. Кожному учню надається алгоритм застосування інтеграла для розв’язування прикладних задач:

Записуємо зміну невідомої величини за допомогою диференціалів:

df= f’(t) dt

Переписуємо  значення F  у вигляді інтеграла :

F=

Знаходимо  первісну для функції f і обчислимо F  як різницю  значень на кінцях відрізка.

Обчислення інтеграла
m={C}{C}	A={C}{C}	q={C}{C}
Q={C}{C}	S={C}{C}

За наведеним прикладом учні самостійно заповнюють четвертий стовпчик таблиці. У цей час обидва вчителі контролюють записи учнів і в разі необхідності виправляють. Далі спільно перевіряють отриманий результат.

 Самостійна робота

 Клас заздалегідь об’єднується у 5 груп диференційовано.  Парти розставлені парами в довільному порядку. Учителі фізики та математики виступають у ролі консультантів.

Задачі для роботи в групах

Гр 1. Тіло рухається з прискоренням , яке змінюється за законом

 a_x(t)= 3t²- 1.  Яке переміщення  зробить тіло за 4 секунди від початку руху , якщо в початковий момент часу його швидкість дорівнювала 2м/с.

Гр 2. У вертикальному циліндричному резервуарі діаметром D= 9 м знаходиться паливо густиною 800кг/м³.Висота рідини в резервуарі  4м , а загальна висота резервуара 5м . Знайти роботу ,яку необхідно виконати для того , щоб спорожнити резервуар.

Гр 3. Судно водотоннажністю 100т рухається прямолінійно зі швидкістю 10м/с. Сила опору води пропорційна швидкості судна Foп_х= - kV_x , де k=6кНс/м. За який час після зупинки двигуна швидкість судна дорівнюватиме 3м/с ?

Гр 4.Матеріальна точка масою  2кг знаходиться на продовженні осі тонкого однорідного стрижня масою 15кг , довжиною 3м  , на відстані 1м від його лівого кінця. Визначити силу гравітаційного притягання стрижня й тіла.

Гр 5. Знайти кількість теплоти , необхідну для нагрівання 1кг заліза від 20⁰С до 25⁰С. Питома теплоємність заліза виражається залежністю : с=452+ 0,425t⁰, де t⁰-температура.

На кінцевому етапі представники груп звітують біля дошки про виконану роботу. Учні слухають відповіді та ставлять питання.

Рефлексія

Спільно підбиваємо підсумок виконаної роботи : чи досягли ми поставленої мети ? Чи проблемні питання вдалося розв’язати на цьому уроці? Чи сподобалася така форма роботи? На що варто звернути увагу вчителям під час організації таких уроків?

 

Домашнє завдання

Розв’язати задачі за обраним рівнем.

Початковий рівень: Знайдіть кількість заряду , що протікає через поперечний переріз провідника за час від t=0 до t=п/2секунд, якщо сила струму  змінюється за законом : i= cos t.

Тіло рухається уздовж осі  Ox за законом:  x= 2t – 1/t. Знайти прискорення тіла в момент часу t=2c/

Тіло обертається навколо осі за законом : ф= t+2t²  рад. Знайти миттєву кутову швидкість у момент часу 1,2с.

Середній рівень:  Тіло рухається прямолінійно .На початковий момент часу 1с його швидкість дорівнює 1м/с , а потім зменшується за законом : Ʋ_x=1- t². Знайдіть довжину шляху , пройденого тілом за 2с від початкового моменту часу.

Достатній рівень: Тіло масою 6кг рухається за законом: S_x= t²_- 3t+2. Знайдіть кінетичну енергію тіла за 10 секунд після початку руху.

Високий рівень: Сила струму в ідеальному коливальному контурі змінюється за законом: і= -0,01sin2t. Який заряд буде на обкладках конденсатора за час п/6 секунд? У момент замикання кола максимальний заряд 5 мКл.