Застосування похідної в економіці. Презентація

Застосування похідноїв економічних розрахунках. Роботу виконала. Уманець-Худенець Марія, студентка 1 МСО

Ключові питання проекту. Чи потрібна похідна в реальному життіЯкі задачі економічного змісту можна розв'язати за допомогою похідної

Мета проекту Формування вміння вести дослідницьку роботу. Показати області застосування похідної на практиці( зокрема в економічних розрахунках). Розвиток пізнавального інтересу; навичок колективної праці. Уміти застосовувати набуті знання та вміння для знаходження найбільшого та найменшого значень функції. Розвивати математичну культуру, логіку, мислення.

Етапи проекту

Початковий етап Організація класного колективу. Вибір темидля дослідження. Мотивація діяльності

Організація діяльностіРозбиття дітей на групи і їхні завдання. Працівники консервного заводу. Знаходження оптимальних розмірів консервної банки. Працівники дерево-обробного комбінату. Потрібно витесати балку найбільшої міцності

Пошук інформації

Обробка інформації

Захист проектів

Звіт групи « ТЕОРЕТИКИ»Завдання. Визначити алгоритм розв'язку задач на знаходження найбільших і найменших значень. Встановити типи задач, які розв'язуються за допомогою похідної в економіці

Більшість своїх зусиль людина витрачає на пошук найкращого розв'язання поставленого завдання. Маючи у своєму розпорядженні певні ресурси, людина прагне досягти більш високого життєвого рівня, найвищої продуктивності праці, найменших втрат, максимального прибутку, мінімальних затрат часу. Частину таких завдань можна дослідити за допомогою методів математичного аналізу – це задачі, які зводяться до знаходження найбільшого і найменшого значення функції.

Нехай задано функцію 𝑓  на відрізку 𝑎;𝑏,    що має похідну в кожній точці відрізка. Тоді для знаходження найбільшого і найменшого щначень цієї функції застосовують такий алгоритм: Упевнитись, що заданий відрізок входить в область визначення функції. Знайти похідну. Знайти критичні точки. Вибрати критичні точки, які належать заданому відрізку. Обчислити значення функції в критичних точках і на кінцях відрізка. Порівняти одержані значення і вибрати з них найбільше і найменше.

Для задач із практичним змістом можна застосовувати таку схему. Одну з величин, яку потрібно знайти, позначити через 𝑥За змістом задачі накласти обмеження на 𝑥Ту величину, про яку йдеться, що вона найбільша чи найменша, виразити як функцію від 𝑥. Дослідити одержану функцію на найбільше чи найменше значення Упевнитись, що здобутий результат має зміст для початкової задачі. 

Опрацювавши довідкову літературу, ми ознайомилися із задачами, поширеними в економіці. Серед них найбільше характерні:визначення загальної вартості утримання різних видів транспорту;визначення продуктивності праці;визначення попиту товарів, зміну доходів під час збільшення ціни;визначення витрат підприємств залежно від об'єму продукції, яку випускають;знаходження оптимальних розмірів продукції з найбільшим ( найменшим) об'ємом(площею).

Звіт групи «Працівники консервного заводу»Завдання. Знайдіть за яких умов витрати жерсті на виготовлення консервних банок циліндричної форми заданого об'єму будуть найменшими.

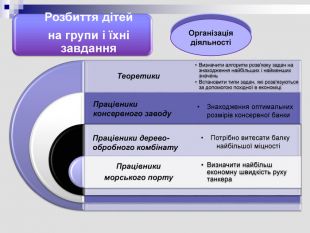
I етап Моделювання. Складемо математичну модель до задачі. Суттєвим є:банка повинна мати заданий об'єм;витрати жерсті повинні бути найменшими( площа поверхні банки, яка має форму циліндра, повинна бути найменшою);розміри банки. Несуттєвим є:конкретна місткість банки;вид консервів(м’ясних, рибних, овочевих) для яких вона призначена.

I етап Моделювання Позначимо діаметр основи банки через 𝒙, висоту через h. Тоді повну поверхню банки виражаємо формулою:𝑺=𝟐∙𝟏𝟒𝝅𝒙𝟐+𝝅𝒙𝒉. Оскільки об'єм банки V відомий, то використовуючи формулу для обчислення об'єму циліндра V=𝟏𝟒𝝅𝒙𝟐𝒉, виражаємо  h через 𝒙:𝒉=𝟒𝑽𝝅𝒙𝟐 Тоді 𝑺=𝟏𝟐𝝅𝒙𝟐+𝝅𝒙∙𝟒𝑽𝝅𝒙𝟐=𝝅𝒙𝟑+𝟖𝑽𝟐𝒙, 𝒙≥𝟎 Завдання: визначити найменше значення функції S=f(x) напроміжку 𝟎<𝒙<∞  

II етап Розв'язання всередині математичної моделі Знаходимо похідну: 𝑺/=𝟑𝝅𝒙𝟐∙𝟐𝒙−(𝝅𝒙𝟑+𝟖𝑽)∙𝟐𝟒𝒙𝟐=𝝅𝒙𝟑−𝟒𝑽𝒙𝟐 Знаходимо критичні точки з умови: 𝑺/=0, 𝝅𝒙𝟑−𝟒𝑽𝒙𝟐=0  Звідси 𝒙=𝟑𝟒𝑽𝝅 Дослідимо знак похідної зліва і справа від критичної точки. При 𝑥𝜖(0; 𝟑𝟒𝑽𝝅) 𝑺/<𝟎,  а при 𝑥𝜖( 𝟑𝟒𝑽𝝅; +∞) 𝑺/>𝟎. Отже, у точці 𝒙=𝟑𝟒𝑽𝝅 функція S(x) має мінімум. Оскільки рівняння не має інших коренів, то цей мінімум збігається з найменшим значенням функції на проміжку( 0; ∞)  

Отже, x=h= 𝟑𝟒𝑽𝝅. Тобто площа повної поверхня циліндра з об'ємом V буде найменшою, якщо циліндр буде рівносторонній. Отже, найменші витрати жерсті на виготовлення консервної банки циліндричної форми будуть за умови, що діаметр основи дорівнюватиме висоті банки.𝐒=𝛑∙𝟒𝐕𝛑+𝟖𝐕𝟐𝟑𝟒𝐕𝛑=𝟔𝐕𝟑𝟒𝐕𝛑=3𝟑𝟐𝛑𝐕𝟐 III етап. Критичне осмислення здобутого результату. Коли 𝒙=𝟑𝟒𝑽𝝅 , то повна поверхня буде найменшою. При цьому h= =𝟒𝑽𝝅𝒙𝟐;  h=4𝑉𝜋3(4𝑉𝜋)2 = 𝟑𝟒𝑽𝝅 

Дослідження продукції марки « Чумак»( зелений горошок, кукурудза, квасоля з овочами)Ці консерви упаковані у жерстяні банки , у яких 𝑥=h=8,3 см. Є також банки, що відповідають Державному стандарту з 𝑥=7,4 см. Для банок з 𝑥=h=8,3 см маємо : S=3∙32𝜋∙4492≈325(𝑐м2)Якщо ж 𝑥=7,4 см, то h=4𝑉𝜋𝑑2, h=4∙449𝜋∙7,42=10,4см2𝑆=𝜋∙7,4(3,7+10,4)≈328(см2)Як бачимо, площа поверхні збільшилась на 3см2, тобто на 1%. Враховуючи, що у нашій країні щорічно виготовляють сотні мільйонів банок консервів у жерстяних банках. Не всі вони мають форму рівностороннього циліндра, тобто на їх виготовлення передбачається збільшення витрат жерсті. Економія 1 % жерсті на виготовлення кожної банки дасть можливість за рахунок зекономленого матеріалу додатково виготовити тисячі нових банок.  

Звіт групи «Працівники деревообробного комбінату»Завдання. З круглої колоди, діаметр перерізу якої дорівнює d, потрібно витесати балку найбільшої міцності. Міцність балки пропорційна 𝒙𝒚𝟐,де - 𝒙 довжина основи прямокутника, який є перерізом балки, а у —його висота. 

I етап Моделювання. Ми з'ясували, що на міцність балки впливають діаметр колоди, форма і розміри перерізу, вид деревини, з якого виготовили балку. Пропонуємо до розв'язку задачу, коли не враховується вид деревини. Позначимо міцність через М, а коефіцієнт пропорційності через k(k>0)За умовою задачі М=𝒌𝒙𝒚𝟐 

Сформулюємо математичну задачу: « При яких значеннях змінних 𝒙 і y функція М набуде найбільшого значення.» 

ОЩАВСДОРК𝒚𝟐=𝒅𝟐−𝒙𝟐, тоді 𝑴𝒙=𝒌𝒙(𝒅𝟐−𝒙𝟐), 𝑴𝒙=𝒌𝒅𝟐𝒙−𝒌𝒙𝟑, 𝒙𝝐𝟎;𝒅. Знаходимо похідну по 𝒙 поданої функції: М/(𝒙)= 𝒌𝒅𝟐-3𝒌𝒙𝟐=𝒌(𝒅𝟐-3𝒙𝟐). Знаходимо критичні точки:𝒌(𝒅𝟐-3𝒙𝟐)=0; 𝒅𝟐=3𝒙𝟐; 𝒙𝟐=𝒅𝟐𝟑; 𝒙=∓𝒅𝟐𝟑;𝒙=−𝒅𝟑 або 𝒙=𝒅𝟑. Перший корінь не належить області визначення функції. II етап Розв'язання всередині математичної моделі

Другий корінь 𝒙=𝒅𝟑 розбиває її на два проміжки:𝟎;𝒅𝟑,𝒅𝟑;𝐝При 𝒙𝝐 𝟎;𝒅𝟑 М/(𝒙)>𝟎. Отже, функція  М(х) зростає в кожній точці цього проміжку. При 𝒙𝝐 𝒅𝟑;𝐝 М/(𝒙)<𝟎 , а отже, на цьому проміжку функція спадає. Таким чином, у точці 𝒙=𝒅𝟑 функція має максимум, який у нашому випадку збігається з її найбільшим значенням.  

Знаходимо 𝒚 :𝒚𝟐=𝒅𝟐−𝒅𝟐𝟑=𝟐𝒅𝟐𝟑 ; 𝒚=𝟐𝟑𝒅. Отже, функція М набуває найбільшого значення при𝒙=𝒅𝟑 і 𝒚=𝟐𝟑𝒅. Міцність балки при цих розмірах буде найбільшою і становитиме: М=𝒌𝒅𝟑∙𝟐𝟑𝒅𝟐=𝟐𝒌𝒅𝟑𝟑𝟑.  

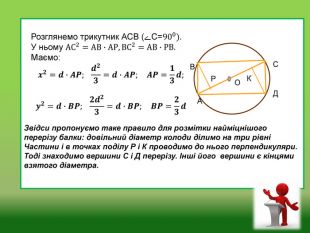
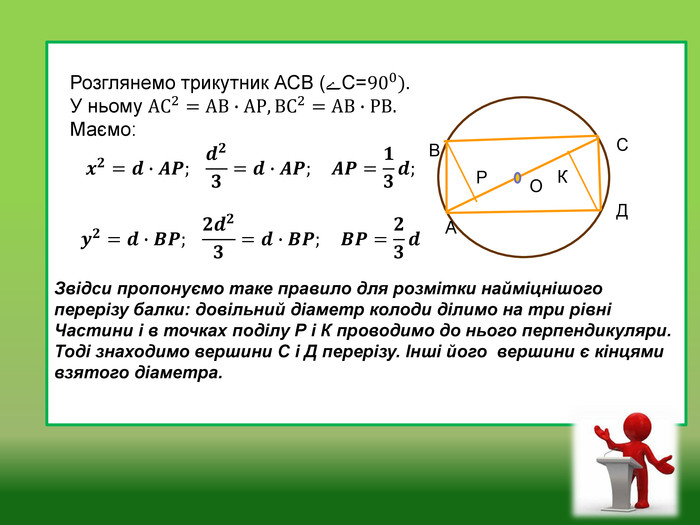
ОЩАВСДОРКРозглянемо трикутник АСВ (ﮮС=900). У ньому АС2=АВ∙АР, ВС2=АВ∙РВ. Маємо:𝒙𝟐=𝒅∙𝑨𝑷;   𝒅𝟐𝟑=𝒅∙𝑨𝑷;    𝑨𝑷=𝟏𝟑𝒅;𝒚𝟐=𝒅∙𝑩𝑷;   𝟐𝒅𝟐𝟑=𝒅∙𝑩𝑷;    𝑩𝑷=𝟐𝟑𝒅 Звідси пропонуємо таке правило для розмітки найміцнішого перерізу балки: довільний діаметр колоди ділимо на три рівні Частини і в точках поділу Р і К проводимо до нього перпендикуляри. Тоді знаходимо вершини С і Д перерізу. Інші його вершини є кінцями взятого діаметра.

Проведемо дослідження. Нехай перерізом балки є квадрат за стороною 𝒙. Тоді 𝑴𝟏=𝒌𝒙𝟑;𝒙=𝒅𝟐; 𝑴𝟏= 𝒌𝒅𝟑𝟐𝟐.𝑴𝟏𝑴∙𝟏𝟎𝟎%=(𝒌𝒅𝟑𝟐𝟐:𝟐𝒌𝒅𝟑𝟑𝟑)∙𝟏𝟎𝟎%=𝟑𝟑𝟐𝟐∙𝟏𝟎𝟎%≈𝟗𝟏,𝟗%Бачимо: якщо переріз колоди буде квадратом зі стороною 𝒅𝟐, то міцність балки порівняно з найбільшою знизиться більше ніж на 8%.  

Зменшення міцності балки при розмірах прямокутного перерізу , відмінних від оптималь-них,означає, що балка або не витримає наван-таження, або термін її використання буде меншим, ніж при 𝑥=𝑑3 і 𝑦=23𝑑, а це економічно не вигідно. Рекомендуємо результати досліджень цієї задачі використовувати будівельникам, столярам, а також тим людям , які роблять замовлення. 

Завдання. Об'єм продукції 𝒖,  яку виробляє бригада робітників, можна описати рівнянням 𝒖=−𝟓𝟔𝒕𝟑+𝟏𝟓𝟐𝒕𝟐+𝟏𝟎𝟎𝒕+50 (од.)𝟏≤𝒕≤𝟖, де 𝒕 – робочий час у годинах. Обчислити продуктивність праці, швидкість і темп її змінювання через годину після початку роботи і за годину до її закінчення.  

Розв'язання. Продуктивність праці виражають похідною:𝒛𝒕=𝒖/(𝒕)=−𝟓𝟐𝒕𝟐+𝟏𝟓𝒕+𝟏𝟎𝟎 ( од./год),а швидкість і темп зміни продуктивності – відповідно похідною 𝒛/(𝒕) і Т(t)=𝒛/(𝒕𝒛(𝒕). Отримаємо: 𝒛/(𝒕)=-5t+15(oд/год𝟐),Т(t)=𝒛/(𝒕𝒛(𝒕)=−𝟓𝒕+𝟏𝟓−𝟓𝟐𝒕𝟐+𝟏𝟓𝒕+𝟏𝟎𝟎=𝟐𝒕−𝟔𝒕𝟐−𝟔𝒕−𝟒𝟎(од./год) 

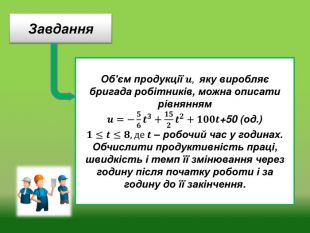
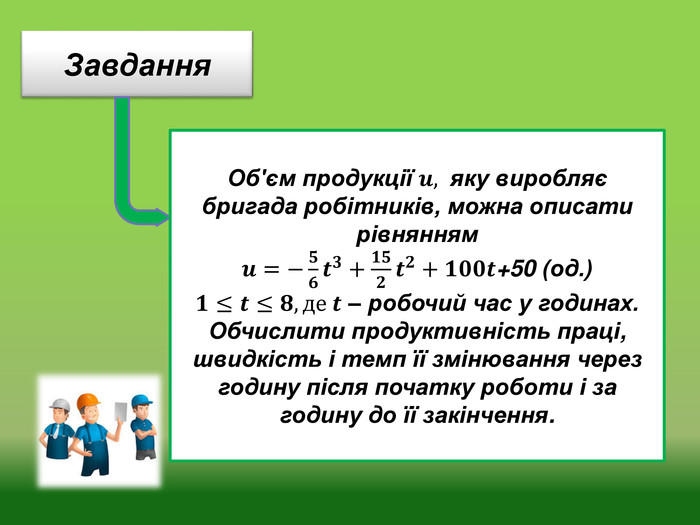
У подані моменти часу 𝒕𝟏=𝟏, 𝒕𝟐=𝟖−𝟏=7 маємо:𝒛𝟏=112,5 (од./год), 𝒛/(1)=10(oд/год2),T(1)=0,09(од./год), z(7) =82,5(од./год), 𝒛/(7)=-20(oд/год2 ), T(7)=-0,24 (од./год). Отже, до кінця роботи продуктивність праці знижується,при цьому зміна знаку 𝒛/(𝒕) і Т(𝒕) з плюса на мінус свідчить про те, що збільшення продуктивності праці у першу годину робочого дня змінюється з її пониженням в останню годину. 

Звіт групи «Працівники морського порту» Завдання. Витрати на паливо,що необхідне для руху танкера, пропорціональні кубу його швидкості та складають 20 у.о. за годину за швидкість 10 вузлів( вузол дорівнює морські милі за годину), а всі інші витрати складають 100у.о. за годину. Знайдіть найбільш-економну швидкість руху за тихої погоди. Обчисліть додатковий прибуток, якщо відстань до порту призначення 100 морських миль( морська миля-1852 м).

Розв'язання. Нехай 𝒙 вузлів – найбільш економна швидкість океанського лайнера, 𝟐𝟎𝟏𝟎𝟑𝒙𝟑=𝟎,𝟎𝟐𝒙𝟑 (у.о.) – витрати палива за швидкості 𝒙 вузлів; 𝟏𝟎𝟎𝒙(год) – час руху, за який танкер пройде 1000 морських миль. Складемо функцію витрат коштів за один рейс:𝑷=𝟏𝟎𝟎𝟎∙𝟎,𝟎𝟐𝒙𝟑𝒙(у.о.)  I етап Моделювання

Враховуючи й інші витрати, що складають 100 у.о. за годину, дістанемо:𝑷=𝟏𝟎𝟎𝟎∙(𝟎,𝟎𝟐𝒙𝟑+𝟏𝟎𝟎)𝒙(у.о.)Завдання: дослідити функцію на найменше значення. 

II етап Розв'язання всередині математичної моделіТреба знайти 𝒙 при якому функція P=𝑓(𝑥) набуває найменшого значення.𝑃/(𝑥)=10000,02𝑥2+100𝑥/=10000,04𝑥−100𝑥2𝑃/(𝑥)=0;10000,04𝑥−100𝑥2=0;0,04𝑥3=100;  𝑥=32500;    𝑥≈13,6 

𝑷/(10)=1000𝟎,𝟎𝟒∙𝟏𝟎−𝟏𝟎𝟎𝟏𝟎𝟐<𝟎;𝑷/(15)=1000𝟎,𝟎𝟒∙𝟏𝟓−𝟏𝟎𝟎𝟏𝟓𝟐>𝟎. Отже, 13,6 вузлів є найбільш економною швидкістю 

Обчислимо витрати коштів на 100 морських миль за швидкості 10 та 13,6 вузлів.𝑷/=𝟏𝟎𝟎𝟎(𝟎,𝟎𝟐∙𝟏𝟎𝟑+𝟏𝟎𝟎)𝟏𝟎=𝟏𝟐𝟎𝟎𝟎(у.о.)𝑷/=𝟏𝟎𝟎𝟎(𝟎,𝟎𝟐∙𝟏𝟑,𝟔𝟑+𝟏𝟎𝟎)𝟏𝟑,𝟔≈𝟏𝟏𝟎𝟑𝟎(у.о.)Рд.п.− додатковий прибуток за один рейс у 100 морських миль. Рд.п.=Р𝟏−Р𝟐;  Рд.п.≈𝟏𝟐𝟎𝟎𝟎−𝟏𝟏𝟎𝟑𝟎=𝟗𝟕𝟎у.о. Отже, 13, вузлів найбільш економна швидкість, 970 у.о. додатковий прибуток. 

Коли 𝑥→∞  або 𝑥→0, то Р→∞. Це означає, що дуже мала і дуже велика швидкості не дають найменшої суми утримання судна на 1 милю шляху, бо за малої швидкості на одну милю шляху витрачається багато часу і, отже, підвищується вартість утриманння команди. За дуже великої швидкості витрачається багато палива.  𝑷=𝟏𝟎𝟎𝟎∙(𝟎,𝟎𝟐𝒙𝟑+𝟏𝟎𝟎)𝒙 

ВИСНОВКИ