Завдання ЗНО математика

                                              Завдання ЗНО 2020

Завдання 1-20 мають по пʼять  варіантів відповіді,серед яких лише  один правильний.Виберіть правильний варіант відповіді

1 Чому дорівнює значення виразу   log₅ ( 25b), якщо  log₅ b= 5?

А)  125            Б)3              В)  7            Г) 30        Д)25

2 Скільки парних п’ятизначних  чисел,усі цифри якого різні, можно записати, використовуючи цифри 3,4,5,7 і9?

А)  24                 Б)  12                  В) 120                 Г) 60          Д) 80

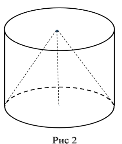
3  Знайти об'єм циліндра, описаного навколо конуса (рис.2), якщо                     

 об'єм конуса дорівнює  15см².

4  Подати у вигляді степеня вираз .

А);   Б) ;    В) ;  Г) .

5. Порівняти і .

А) >;   Б) = ;  В) < ;   Г)  порівняти неможливо.

6 Обчислити значення виразу .

7  Виберіть для функції    у= 5х⁴   первісну,графік якої проходить через точку А(–1;3).

А)  F(x)=20x³+23 Б) F(x)=x⁵+3     В) F(x)=x⁵         Г) F(x)=x⁵+4      Д) F(x)=x⁵+2

8. Графіку якої з наведених функцій належить точка А(8;2)?

А);   Б);    В) у=х³;      Г) у=log₂ x    Д)  у=х²

9. У шафі лежить 10 зелених, кілька чорних і кілька сірих пар шкарпеток. Скільки чорних і скільки сірих пар шкарпеток у шафі, якщо ймовірність навмання взяти пару чорних шкарпеток дорівнює 0,3, а сірих – 0,2?

10. Площа основи циліндра дорівнює 64π см², а його висота - 10 см. Обчислити бічну поверхню циліндра.

А) 160π см²          Б) 480 см²                  В) 321π см²         Г) 80π см²              Д) 320π см²

11. Графік функції у=2^х перенесли паралельно на 3 одиниці вправо вздовж осі абсцис і на 4 одиниці вгору вздовж осі ординат. Графік якої функції було отримано?

       А) у=2^х–3 – 4; Б) у=2^х–3 + 4;          В) у=2^х+3 + 4;     Г) у=2^х+3 – 4       Д) у=2^х–3 ; 

12. Якого найбільшого значення може набувати функція f(х)=3сos4х1

      А) 11      Б) 2   В) 4  Г) 1           Д) 8

13. У якій координатній чверті знаходиться вершина параболи у=(х+8)²12?

А) у І чверті;      Б) у ІІ чверті; В) у ІІІ чверті;      Г) у ІV чверті      Д)  І і ІІ чверті

14.Знайти відстань   від точки  А(2;-3;6)  до площини    хОу.

А)  2        Б)    - 3                В)      6                  Г)    -6               Д) 4

15. Основи  і бічна сторона  рівнобедреного трикутника  відповідно дорівнюють  16см і 10см. Знайти  висоту трикутника,проведену до бічної сторони.

   А)34см            Б)6см             В) 8см          Г) 9,6см             Д) 4,8см

16. Яка область визначення функції ?

   А) (∞;3];  Б) [3; ∞); В) (3;∞);  Г) (∞;3).

17.У трикутнику   MNK     MN=k, NK= m,  MK=n,  NL-бісектриса  трикутника. Знайти довжину відрізка  ML.

18.Відомо, що ctg˂0,  Cos> 0. Якого значення   може набувати  Sin?

А)   –1             Б) –             В)  0                          Г)                    Д) 1

19. Площа основи конуса дорівнює 36 см2, а його твірна - 10 см. Обчислити бічну поверхню конуса.

А) 360π см²       Б) 36π см²           В) 60π см²          Г) 180π см²         Д) 120π см²

20. Контейнер для сміття має форму циліндра, висота якого 1 м, а радіус основи 40 см. Вкажіть скільки фарби потрібно, щоб пофарбувати всю поверхню контейнера, якщо на 1 м² поверхні витрачається 100 г фарби:

А) 11,2 г           Б) 40 г             В) 112 г               Г) 72 г                    Д) 7,2 г

Завдання 21-24 установити відповідність.

21. Установити відповідність між виразами (1–4) і числами (А–Д), що є значеннями даних виразів:

1.     А –3

2. log₄2+log₄8    Б –2

3.       В 3

                                                                        Г 2

                                                                         Д  5

22. У прямокутній системі координат на площині  ху задано точки О(0;0) і А(6;8). З точки А на вісь  х опущено перпендикуляр. Точка В– основа цього перпендикуляра. Установіть відповідність  між величинами (1-4) та їхніми числовими значеннями  (А-Д)

1.Довжина вектора  ОВ                                                    А  4

2.Відстань від точки А до осі  х                                       Б   5

3.Ордината точки М-середини відрізка АВ                   В  6

                                                                                             Г 8

                                                                                             Д 24

23.Установити відповідність між функціями та їх областями значень:

1.      А

2.                  Б [3; 7]

3.                            В [1; 5]  

                                                                                                Г [–1; 3]

                                                                                                Д [1; 9]

24. Установити відповідність між заданими многогранниками (1-4) та кількістю їх граней (А-Д)

1. Трикутна призма                                       А 4

2. Шестикутна призма                                   Б 5

3.Пʼятикутна піраміда                                   В 6

                                                                         Г  7

                                                                         Д  8

Завдання   відкритої форми структуроване   завдання   25-27   

25. Дано вектори (2;-1;1)  і (-4; х+1 ;-2).

1. При якому значенні х вектори перпендикулярні?

2. При якому значенні х вектори колінеарні?

26.Вкладник поклав  до банку на два різні рахунки загальну суму 1500 грн. По першому з них банк виплачує 7% річних,  а по другому банку  10% річних. Через рік вкладник отримав 120 грн відсоткових грошей.

1) Скільки гривень він поклав на перший рахунок?

2)Скілько всього гривень вкладник отримав через рік по двох вкладах?

27.  Дано функції    f(x)= 2^x–8,   g(x)= x²–4x +3.

1.Розвʼязати   рівняння   .У відповідь  записати кількість розв’язків рівняння.

2. Розвʼязати нерівність   f(x)∙ g(x)>0. У відповідь записати добуток усіх натуральних  чисел,які не розвʼязками нерівності.

28. Турист проплив  на моторному човні 30км проти течії річки і повернувся назад  на плоту. Знайдіть швидкість течії річки,якщо на плоту турист плив на 3год більше, ніж  човном,а власна швидкість човна становить 15км/ год.

29. Основою піраміди є рівнобедрений трикутник з висотою 9см й  основою 6см.Кожне з бічних ребер піраміди дорівнює 13см. Знайти  у сантиметрах висоту піраміди.

30. Імовірність того,що Петрик розв’яже  задачу,дорівнює 0,7, а ймовірність того,що задачу розв’яже Михайлик, дорівнює 0,8.Знайти ймовірність того, що  жоден  з них не розв’яже  цю задачу.

31. Пряма, паралельна до сторони АВ трикутника АВС, перетинає його  сторону АС у точці Е,а сторону ВС – у точці F. Знайти площу у (см²)  трикутника СЕF,якщо АЕ: ЕС=3:2,а площа трикутника дорівнює 75см².

32.  Задано фігуру, де пари (х;у) задовольняють умову   х²+у² ≤ 6х –8у–24.

1.Виділть повний квадрат у виразі х²-6х;

2.Виділіть повний квадрат у виразі у²+8у;

3.Зобразіть фігуру,яка задана рівнянням  х²+у²  = 6х –8у–24.

33.Через вершину конуса під кутом до площини основи проведено переріз, який перетинає  основу конуса по хорді,що стягує дугу .Знайдіть площу перерізу,якщо висота конуса дорівнює Н.

34. Радіус основи конуса дорівнює 5. Осьовим перерізом  конуса є прямокутний трикутник. Знайти 1.  площу  S  бічної поверхні конуса;

2.обʼєм конуса .

У відповідь записати 1)     2)

35. Указати значення параметра  а , за якого  система     ах +3у= 9;  має безліч розв’язків.

                                                                                                    3х–4у= -5.