Застосування проблемного навчання на уроках математики

ЗМІСТ

 

ВСТУП…………………………………………………………………………………….4

 

РОЗДІЛ  1. ТЕОРЕТИЧНІ  ОСНОВИ ЗАСТОСУВАННЯ ТЕХНОЛОГІЇ ПРОБЛЕМНОГО НАВЧАННЯ………………………………………………………..6

1.           Зміст і роль технології проблемного навчання………....................................6
2.           Особливості застосування проблемного навчання на уроках математики........................................................................................................10

 

РОЗДІЛ 2. МЕТОДИЧНІ АСПЕКТИ ЗАСТОСУВАННЯ ТЕХНОЛОГІЇ ПРОБЛЕМНОГО  НАВЧАННЯ  МАТЕМАТИКИ………………………………...13

1. Педагогічний досвід застосування технології проблемного навчання на уроках математики..……………….......................................................................13
2. Методичні вимоги й рекомендації щодо організації проблемного навчання уроках математики  ………………………………………………………….......21

 

ВИСНОВКИ……………………………………………………………………………..24

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ…………………………….........................26

ДОДАТОК……………………………………………………………………………….28

 

 

ВСТУП

 

  Актуальність  теми проекту.  Практика навчання у закладах освіти та психолого-педагогічні дослідження довели необхідність відмовитися від уявлень про навчально-виховний процес як процес повідомлення і передачі інформації.

Роль сучасного вчителя не лише в тому, щоб ясніше, зрозуміліше, ніж у підручнику, повідомити учням інформацію, а в тому, щоб стати організатором пізнавальної діяльності, у якій головним суб'єктом у  системі  «педагог-учень» стає саме учень. Цим вимогам відповідають інноваційні  педагогічні  технології  під якими розуміємо нові, оригінальні технології (методи, засоби, способи) створення, передавання і збереження навчальних матеріалів, інших інформаційних ресурсів освітнього призначення, а також технології організації і супроводу навчального процесу (традиційного, електронного, дистанційного, мобільного) за допомогою телекомунікаційного зв’язку і комп’ютерних мереж, що цілеспрямовано, систематично й послідовно впроваджуються в освітню практику.

Однією з перспективних інноваційних технологій є проблемне  навчання, сутність його полягає в тому, що воно ґрунтується не на передачі готової інформації, а на отриманні учнями певних знань і умінь шляхом вирішення теоретичних і практичних проблем в процесі самостійної дослідницької  діяльності.

На жаль, сьогодні проблемне навчання є швидше теоретичною моделлю розвиваючого навчання, ніж реалізується на практиці як цілісний процес. Основні положення технології проблемного навчання недостатньо методично конкретизовані, не розроблені  чисельні питання її доцільного застосування. Тому проблемне навчання у сучасній школі, зокрема на уроках математики, використовується епізодично і, як правило, не завжди ефективно.

Отже, застосування технології проблемного навчання на уроках математики є актуальною темою у сучасній педагогічній науці й методиці.

Аналіз  наукових досліджень та публікацій.  Ідеї проблемного навчання набули поширення в 70-80 рр. ХХ ст. в працях провідних психологів та дидактів: І.Лернера, Т.Кудрявцева, А.Матюшкіна, М.Махмутова, В.Оконя та ін.

За В. Оконем, майстерність педагога передусім виявляється в організації проблемних ситуацій [9, с. 15].

 Дещо інакше підходить до визначення змісту проблемного навчання І. Лернер, який робить наголос на творчому вирішенні проблеми, творчому засвоєнні знань і умінь, формуванню активності високо розвиненої особистості [9, с.16].

На сучасному етапі розвитку освіти розробці методики і технології проблемного навчання істотно сприяють наукові дослідження О. Топузова.

Загалом дослідження вчених свідчать про високу ефективність проблемного навчання, яке впливає на рівень мислення учнів, їх самостійність і творчість.

Об’єкт проекту: уроки математики.

Предмет проекту: технологія проблемного навчання на уроках математики.

Мета проекту: дослідити методичні особливості застосування технології проблемного навчання при вивченні математики.

Завдання проекту.

1. Уточнити  зміст  основних понять авторського проекту: «проблемне навчання», «проблемний метод» у науково-методичній  літературі.
2. Визначити особливості застосування технології проблемного навчання на уроках математики.
3. Розкрити методичні аспекти реалізації технології проблемного навчання на уроках математики.
4. Окреслити методичні вимоги й рекомендації щодо організації проблемного навчання уроках математики.

РОЗДІЛ  1

ТЕОРЕТИЧНІ  ОСНОВИ  ЗАСТОСУВАННЯ  ТЕХНОЛОГІЇ  ПРОБЛЕМНОГО НАВЧАННЯ

 

1.           Зміст і роль технології проблемного навчання

 

Проблемне навчання – це така організація навчального процесу, яка передбачає створення під керівництвом педагога проблемних ситуацій і активну пізнавальну діяльність учнів для їх вирішення, у результаті чого відбувається творче оволодіння  знаннями, навичками, вміннями, розвиток розумових здібностей.

Проблемне навчання є певним протиставленням традиційним технологіям навчання. Основний недолік традиційного навчання – це слабка реалізація розвиткової  функції  навчального процесу, тому що навчальна діяльність учнів  має переважно репродуктивний (відтворювальний) характер. Під час проблемного навчання педагог не дає готових знань, а організовує їх пошук учнями шляхом спостереження, аналізу фактів, активної розумової діяльності.

Проведемо порівняльну характеристику традиційного і проблемного навчання (табл. 1)6, с. 6.

Таблиця 1.

Порівняльна  характеристика  традиційного і  проблемного  навчання

Традиційне навчання	Проблемне навчання
Навчальний матеріал подається у готовому вигляді. Педагог основну увагу звертає на програму навчання, дотримання її вимог, оцінювання учнів.	Новий навчальний матеріал учні отримують під час вирішення теоретичних і практичних проблем, в процесі пошукової, дослідницької, самостійної діяльності.
Під час учіння виникають певні прогалини, перепони й труднощі, викликані тимчасовим вилученням учня з процесу навчання. Контроль навчальних досягнень тільки частково пов’язаний з процесом навчання: він не є складовою цього процесу.	Під час вирішення проблемної ситуації учні навчаються самостійно долати труднощі. Підвищена пізнавальна активність учнів сприяє розвитку позитивних мотивів навчальної діяльності, зменшує необхідність формальної перевірки результатів.
Темп навчання залежить від навчальної програми.	Темп навчання залежить від індивідуально-психічних якостей учнів. Вчитель створює  різні дидактичні ситуації, що відповідають особливостям тих, хто вчиться, їх рівню знань та інтелектуальним можливостям.
Відсутність можливості досягнення більшістю учнів високих навчальних результатів; найбільше утруднення викликає використання й застосування отриманих знань й інформації на практиці.	Результати навчання є достатньо високими та стійкими. Учні з легкістю використовують отримані знання на практиці та водночас розвивають свої вміння й здібності.

 

Отже, головна особливість проблемного навчання  пошукова, дослідна діяльність учнів. При цьому знання не даються в готовому вигляді, а ставиться проблема для самостійного вирішення. Найбільш суттєвою рисою проблемного навчання є не постановка запитань, як думає більшість вчителів, а створення навчальних проблемних ситуацій.  

Відтак  суть проблемного навчання зводиться  до створення  такої ситуації, яка змушує учня, спираючись на отримані знання, самостійно шукати рішення. Але такі ситуації не виникають самі, а стають результатом дидактичної майстерності педагога. Так, педагог М. Фіцула наголошує, що «використання теоретичних та експериментальних завдань ще не робить навчання проблемним. Все залежить від того, наскільки вчителеві вдається надати цим завданням проблемного характеру і поєднувати проблемний підхід із іншими методичними підходами 16, с. 54».

В  проблемному  навчанні виділяють навчальну  проблему, проблемні ситуації, задачу і запитання.

Навчальна проблема не тотожна  науковій  проблемі. Її  особливість  у  тому, що її рішення відоме науці, але невідоме учням. Головною ознакою навчальної проблеми є наявність суперечливої  інформації  або  ситуації.

За  способом розв'язання виділяють такі проблеми:

1) фронтальна  проблема, яку ставлять перед усім класом і вирішують зусиллями всіх учнів;

2) групова  вирішується окремою групою учнів. Групи можуть розв'язувати одну загальну або кожна свою окрему проблему;

3) індивідуальна  проблема, яку ставить сам учень або вчитель, але, як правило, вирішує учень самостійно [14, с. 167].

Проблемна ситуація  ситуація, для оволодіння якою учень або колектив мають знайти й застосувати нові для себе знання чи способи дій.

Вдало створена проблемна ситуація є важливою ланкою наступного засвоєння школярами знань проблемним шляхом, що складається з таких етапів:

1) організація проблемної ситуації (педагог  створює проблемну ситуацію, учень  усвідомлює суперечності у навчальному матеріалі, який вивчається);

2) формулювання проблеми (педагог  організовує обміркування  проблеми та її формулювання, учень   формулює навчальну проблему);

3) індивідуальне або групове вирішення проблеми суб'єктами учіння (педагог  організовує вирішення проблеми, формулювання гіпотези, учень  висуває гіпотезу, яка пояснює досліджувану навчальну проблему);

4) верифікація (перевірка, тлумачення і систематизація) отриманої інформації (педагог  організовує перевірку гіпотези, учень  перевіряє гіпотезу шляхом експерименту, вирішення завдань, наукового пошуку тощо);

5) використання засвоєних знань у теоретичній та практичній діяльності (педагог  організовує узагальнення результатів попередніх дій і використання здобутих знань на практиці, учень  аналізує отримані результати. Формулює висновки, використовує їх у практичній діяльності) [13, с. 32].

Зазначимо, що між навчальною проблемою та проблемною ситуацією чіткої межі немає. Навчальна проблема передбачає її вирішення або наявність правильної відповіді. Проблемна ситуація не завжди має вирішення на рівні сучасних знань.

Проблемні задачі та запитання створюють навчальні проблеми та ситуації. Підкреслимо, що запитання  й задачі можуть бути і не проблемними. Проблемними вони стають лише тоді, коли в своїй суті несуть інформацію, раніше невідому учневі, їх не можна вирішувати як типові.

Таким чином, проблемна задача  це центральне поняття проблемного навчання, яке припускає наявність проблемної ситуації. Проблемне запитання  це вираз протиріччя між знанням та незнанням, спонукання до пізнання нового.

Проблемне навчання, на думку В. Ягупова, має свої недоліки: його не завжди можна використовувати через складність матеріалу, що вивчається; непідготовленість суб'єктів навчального процесу [18, с. 196].

Звісно, весь учбовий матеріал практично неможливо засвоювати шляхом розв’язування проблем. По-перше, неоднорідною є структура самих знань, що підлягають засвоєнню, і, по-друге, – процесу навчання, в якому постійно чергуються етапи засвоєння знань, їх повторення і застосування. Напевне, виправдовує себе комплексне використання традиційного та проблемного навчання, які взаємно доповнюють одне одного і компенсують недоліки.

Але проблемне навчання, безперечно, має суттєві переваги. Досвід кращих вчителів підтверджує, що рівень науковості викладання підвищується, якщо дії вчителя спрямовані на формування пізнавальних потреб учнів і на зміни в структурі їх розумової діяльності. Це у сукупності забезпечує засвоєння знань на більш високому рівні абстрактності. Саме з цією метою і потрібно застосовувати проблемний підхід до навчання математики.

Отже, проблемне навчання сприяє не лише набуванню учнями необхідної системи знань, умінь і навичок, але й формування в них здатності до самонавчання, самоосвіти, оскільки засвоєння навчального матеріалу відбувається в ході активної пошукової діяльності школярів, у процесі вирішення ними системи проблемно-пізнавальних завдань. При такому навчанні учні, ознайомлюючись з новим матеріалом, не отримують від вчителя готових знань. Педагог лише створює проблемну ситуацію та надає фактичний матеріал, необхідний для її розв’язання. Вирішуючи питання, які виникають у зв’язку зі змістом цієї ситуації, та використовуючи наведені вчителем відомості, школярі повинні самостійно «відкрити » знання, заплановані навчальною програмою.

 

1.2. Особливості застосування проблемного навчання на уроках математики

 

Основний зміст технології проблемного навчання має становити методика застосування проблемних ситуацій на різних етапах уроку. Під проблемними ситуаціями маємо на увазі такі навчальні ситуації, які виникають у моменти, коли учень сприймає задачу, бажає (намагається) її розв’язати, але відчуває нестачу знань. Такі ситуації викликають активну мисленнєву діяльність  учня, спрямовану на подолання труднощів, тобто на здобуття нових знань, умінь, навичок.

Урок  математики  – ідеальний матеріал для створення проблемних ситуацій. Саме на цих уроках в учнів виникають питання: «Чому?», «Як?», «Звідки?».

Проблемна ситуація в навчанні математики – це пізнавальна трудність, для подолання якої учні мають здобути нові знання або докласти інтелектуальних зусиль. Відомо, якщо активізувати пізнавальну активність школярів, то потреба в нових способах дій стає для них природною й необхідною. Учні самі, того не помічаючи, потрапляють під вплив проблемної ситуації.

Проблемна ситуація при навчанні математики виникає  абсолютно природно, не вимагаючи ніяких спеціальних вправ, штучно підібраних ситуацій. По суті, не тільки кожне текстове завдання, але і половина інших вправ, представлених в підручниках математики, є свого роду проблемними, над вирішенням яких учень повинен задуматися, якщо не перетворювати їх виконання на суто тренувальну роботу, пов’язану з рішенням по готовому, даному вчителем зразку.

Вправи в розв’язанні складних завдань, в порівнянні виразів, що вимагають використання відомих учням закономірностей і зв’язків в нових умовах, вправи геометричного змісту, які часто вимагають переосмислення набутих раніше знань, та інші вправи повинні бути використані для постановки учням проблемних завдань. Тільки в цьому випадку навчання математиці надаватиме дієву допомогу у вирішенні освітніх, виховних і розвиваючих завдань навчання, сприяючи розвитку пізнавальних здібностей учнів, таких рис особистості, як наполегливість в досягненні поставленої мети, ініціативність, уміння долати труднощі.

Доцільність створення проблемних ситуацій очевидна, тому слід відмітити способи створення проблемних ситуацій на уроках математики, запропоновані вченими-дидактами В. Коваленко та І. Тесленко.

1. Підведення учнів до обґрунтування неочевидних залежностей.

2. Пропедевтичні завдання. Такі завдання пропонують перед вивченням нового матеріалу і на уроці, і як домашні. Вони активізують увагу учнів, служать базою для створення проблемних ситуацій і самостійного розв’язування навчальної проблеми.

3. Підведення учнів до самостійних індуктивних висновків.

4. Розв’язання підготовчих вправ та задач.

5. Створення ситуації вибору.

6. Підведення учнів до висновків, що суперечать їх попереднім уявленням.

7. Організація дискусії. Проблемні ситуації виникають тоді, коли вчитель ставить перед учнями проблемне питання й організовує його обговорення.

8. Порівняння нового поняття з вивченим раніше [5, с. 27].

Учений радив, щоб певну проблему вчитель доносив до свідомості учнів так (через систему заздалегідь складених питань, рисунків-підказок, моделей), щоб вони самостійно формулювали цю проблему і знаходили її розв’язок: «Учитель не просто подає готові наукові факти, а здійснює групування і перегрупування навчального матеріалу так, щоб перед учнями виникла проблема або система проблем, внаслідок чого дітей можна було б підвести до науково-пізнавального пошуку, а потім за допомогою системи  питань розкривати внутрішні протиріччя, які виникають в процесі розв’язання проблеми, задачі чи доведення теорем» [5, с. 30].

Досліджуючи проблему розвитку математичних здібностей учнів, Н.Д. Янц наводить типи проблемних ситуацій для  розвитку мислення. Ось деякі з них:

• завдання з несформульованим питанням;
• завдання з відсутніми даними;
• завдання із зайвими даними;
• завдання з кількома рішеннями;
• завдання з мінливим змістом;
• завдання на міркування, логічне мислення [20, с. 149].

Виділимо особливості проблемного підходу до навчання математики:

1) під  час розв’язання навчальних проблем для вчителя значно розширюються можливості формування специфічної інтелектуальної діяльності учнів, яка спрямована на самостійне засвоєння ними нових математичних знань;

2) в учнів виробляються раціональні прийоми логіко-теоретичного мислення та розвиток наукової інтуїції;

3) школярі краще усвідомлюють зв’язок теорії, яка вивчається на уроках математики, з практикою;

4) вчитель має змогу систематично застосовувати різноманітні види самостійної роботи на уроці;

5) перед вчителем постають широкі можливості здійснення диференційованого навчання та індивідуального підходу до учнів;

6) проблема розгортається перед школярами в динамічному розвитку, в органічному зв’язку з попередніх матеріалом;

7) при проблемному навчанні забезпечується оптимальне співвідношення індукції та дедукції, продуктивних і репродуктивних форм навчання;

8) проблемний підхід є ефективним засобом розвитку творчого мислення.

Таким чином, постановка питання про використання проблемних ситуацій не є новою для вчителя, а вимагає лише правильного використання всіх тих ресурсів, які приховані в курсі математики. Впровадження у навчальний процес з математики проблемного навчання, порівняно із так званою «пасивною» моделлю має ряд переваг: учні  засвоюють усі рівні пізнання (знання, розуміння, застосування, аналіз, синтез, оцінку); відсоток засвоєння, як правило, високий; педагог сильніше розкривається перед учнями як особистість, виступає як лідер, організатор; роль учнів активна, вони приймають важливе рішення стосовно процесу навчання; джерело мотивації  внутрішнє (інтерес самого учня).

РОЗДІЛ 2

МЕТОДИЧНІ АСПЕКТИ ЗАСТОСУВАННЯ ТЕХНОЛОГІЇ ПРОБЛЕМНОГО  НАВЧАННЯ  МАТЕМАТИКИ

 

2.1. Педагогічний досвід  застосування  технології проблемного навчання  на уроках математики

 

Завдання вчителя математики  вчити дітей не тільки засвоювати факти, а й розуміти логіку фактів. Постановка проблемного питання у ході вивчення нового матеріалу та пошук розв’язання  проблеми учнями  важливий шлях формування свідомого підходу до навчання математики.

Кожна математична задача має постановку конкретної  проблеми, вираженої  у вигляді запитання. За наявності готового алгоритму можна без особливого дослідження розв’язати задане питання. Якщо алгоритм відсутній, то бажано використати на уроці проблемний метод.

Проблемний метод трансформує в собі концентрацію набутих знань та аналітичний пошук нового способу розв’язання поставленої проблеми. Новий алгоритм фіксують, виділяють та закріплюють у нових ситуаціях.

На прикладі уроків математики покажемо окремі моменти застосування проблемного  методу. Це  може бути цілком логічний  перехід від повторення до постановки теми нового матеріалу. Проблемні запитання можуть виникати під час розв’язування нестандартної задачі, що потребує творчого підходу.

Для вирішення цих завдань використовуємо різноманітні творчі вправи, запитання, цікаві задачі, логічні вправи, задачі-головоломки, задачі-жарти, дидактичні ігри, загадки, ребуси, які в свою чергу передбачають:

• встановлення суперечності;
• встановлення причинно-наслідкових зв’язків;
• встановлення схожості та різниці між об’єктами, що порівнюються;
• зіставлення різних варіантів та дії вибору;
• виділення певних закономірностей в навчальній інформації;
• доведення правильності виконаних практичних або розумових дій;
• пошук і виправлення припущених помилок;
• висування гіпотез, здійснення певного прогнозу наступних подій.  Додаток.

Розглянемо деякі приклади розв’язування творчих  завдань.

Приклад 1. Обчисліть найбільш раціональним способом:

arctg 1 + arctg 2 + arctg 3.

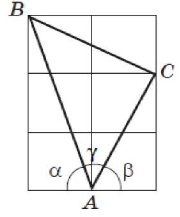Розв’язання. Нова ідея полягає в застосуванні рисунка як графічної моделі розв’язання задачі. Тож зробимо рисунок.

За рисунком видно, що tg а = 3, звідки а = arctg 3;

tg β = 2, звідки β = arctg 2.

Трикутник ABC є прямокутним і рівнобедреним, тому tg  γ = tg 45° = 1, звідки γ = arctg 1.

Отже, arctg 1 + arctg 2 + arctg 3 = π [1, с. 20]

Приклад 2. Потяг проходить відстань від міста А до міста В за 10 год 40 хв. Якби швидкість потяга була на 10 км/год менша, то він прийшов би на 2 год 8 хв пізніше. Знайти відстань між містами та швидкість потяга.

Розв’язання. Розв’яжемо задачу нестандартно  графічно, а не з допомогою складання рівняння, як уже всі давно звикли.

По горизонтальній осі будемо відкладати швидкість потяга, а по вертикальній  час. Оскільки відстань, яку пройшов потяг, рівна  добутку 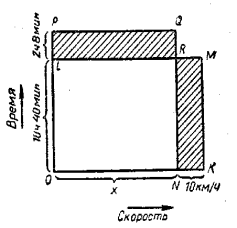швидкості на час, то площа прямокутника, сторони якого відповідно зображають швидкість і час, зобразить відстань, яку пройшов потяг.             

Нехай  відрізок ОК  швидкість поїзда, а відрізок  ОL  час ходу (10 год 40 хв); в такому випадку площа прямокутника OKML зображає відстань між містами А і В. Якщо швидкість потяга зменшиться на 10 км/год (на відрізок KN), то час ходу збільшиться на 2 год 8 хв (на відрізок LP). В цьому випадку відстань АВ зобразиться площею прямокутника ONQP.

Оскільки відстань між містами в обох випадках одна й та ж сама, то площі прямокутників OKML і ONQP мають бути рівними; оскільки прямокутник ONRL  їх спільна частина, то площа прямокутника NKMR має бути рівна площі прямокутника LRQP. Позначивши невідому зменшену швидкість потяга (відрізок ON) через х, отримаємо:

10 год 40 хв  10 = 2 год 8 хв  х  , звідки

х =  10 =  10 = 50

Швидкість потяга: 50+10=60 (км/год).

Відстань між містами: 60 х 10 = 640 км. [19, с. 18].

У шкільному курсі математики є достатньо проблемних завдань, що можуть здивувати та заціка­вити школярів. Наприклад, на уроці алгебри при ви­вченні теми «Множення різниці двох виразів на їх суму» можна спочатку провести усний рахунок під девізом  «Хто швидше?» (знайти добуток двох чисел 21х19; 31x29; 42x38; 45x35; 201х199). Після закінчення усного рахунку слід відмітити, що помножити числа можна швидше, якщо вивчити важливий і цікавий розділ «Формули  скороченого  множення». Учні 7 класу ще не ознайомлені з розкладанням ква­дратного тричлена на множники за загальною формулою, тому задача розкласти на множники a  2a  3 для них є проблемною.

Цікаво, що постав­лена задача може бути розв’язана де­кількома способами. Методично доцільно пояснити це учням так:

1. a² - 2a - 3 = 3a² - 2a² - 2a - 3 = 3(a² -1) - 2a (a + 1) = 3(a - 1) (a +1) - 2a (a +1) = (a + 1) (a - 3).
2. a² - 2a - 3 = a² - 3a + a - 3 = a (a - 3) + (a - 3) = (a – 3)(а+1)
3. a² - 2a - 3 = a² - 2a - 2 -1 = (a² -1) - 2(a + 1) = (a + 1)(a - 3).
4.  a² - 2a - 3 = a² - 2a +1 - 4 = (a-1)² - 2² = (a + 1)(a - 3).

Викликати в учнів інтерес до математики можна й за допомогою нестандартних і доведених прикладів. Крім повідомлення нових фактів, розгляду відомого матеріалу під іншим кутом зору, стимул но­визни може приймати й інші форми. Наприклад, виявлення відомих  за­кономірностей у  результаті безпосередньої дослідницької роботи. Так, на уроці геометрії у 8-у класі перед доведенням теореми Піфагора пропонуємо учням побудувати прямокутний трикутник з катетами а=3 см, в=4 м. Потім виміряти гіпотенузу  з точністю  до  цілих чисел і переві­рити, чи буде виконуватися рівність: а²+в²=с². Учні під керівництвом учи­теля самі формулюють і доводять тео­рему  Піфагора.

Для закріплення мате­ріалу пропонуємо розв’язати задачу: чи існують три послідовних цілих числа, які відподіають теоремі Піфагора? Учні позначають сторони прямо­кутного трикутника n-1, n, n+1 і легко знаходять катети й гіпотенузу.

Після використання теореми Піфагора і перетворення виразу (n -1)²+n²=(n+1)² учні отримують n=4. Числа 3, 4, 5 є довжинами сторін прямокутного трикутника. Розповідаємо учням, що на основі даної тео­реми Піфагор створив правило для знаходження цілих чисел, якими представлені довжини сторін прямо­кутних трикутників за формулами: a = 2n +1; в = 2n²+2n; c = 2n² + 2n +1, де a і  b  катети, c  гіпотенуза. Залучаючи учнів у процес розв’язання проблемних навчальних завдань, навчаємо їх розмірковувати, аналізувати, робити висновки з фактів, тобто виховуємо пізнавальну активність  важливу умову розвитку творчих  здібностей.

Велике значення для розвитку інтелекту та мислення учнів мають проблемні за­дачі з кількома різними способами розв’язання. Д. Пойа стверджував, що краще розв’язати одну задачу кількома спо­собами, ніж кілька різних чи однотипних задач [11, с.45]. Ми також дотримуємося такої думки, тим паче, що розв’язування задач різними способами залучає учнів до пошукової діяльності, створюючи умови для розвитку їх критичного мислення. Цього принципу дотримуємося при порівнянні різних розв’язків  завдань, оцінюванні їх нестандарт­ності, складності в обчисленнях, доступності, новизни.

Розглянемо задачі на спільну роботу, які зустрічаються в курсі  математики  6 класу. У розв’язанні цих задач велику роль відіграють такі величини: частина всієї роботи, яку виконує робітник (бригада, машина) за одиницю часу; час, який було витрачено на роботу; частина роботи, яку було виконано.

Задача №1. Одна бригада може виконати певну роботу за 10 днів, друга  за 15 днів. За скільки днів обидві бригади, працюючи разом, виконають цю роботу?

Розв’язання. 1-й спосіб.  Перша бригада виконує роботу за 10 днів, тобто за 1 день вона виконує   роботи. Друга бригада виконує за 1 день роботи. Це означає, що, працюючи разом, обидві бригади виконають +   частину усієї роботи.

1   6 (днів)  за такий час буде виконана вся робота. Відповідь: вся робота буде виконана за 6 днів. Зверніть увагу: оскільки ми розглядаємо частини роботи, немає сенсу говорити, що всю роботу приймаємо за 1. Цю ж задачу ми можемо розв’язати за допомогою рівняння. Для розв’язування задач цим способом зручно користуватися таблицями. Але це  є  не обов’язковим.

2-й спосіб. Перша бригада виконує роботу за 10 днів, тобто за 1 день вона виконує  роботи. Друга бригада виконує за 1 день роботи. Це означає, що, працюючи разом, обидві бригади виконають всю роботу за х днів:

  + 

=

Звідси маємо: 5x  30, х  6 днів необхідно двом бригадам, щоб впоратись з роботою.

Відповідь: 6 днів.

Розв'язування однієї математичної задачі кількома способами активізує навчальну діяльність школярів, прививає інтерес до предмету. До розв’язування задач декількома способами учнів слід привчати поступово. Можна на уроці розглянути один або два способи, а пошук інших способів  пропонується на домашнє завдання. Можливо, запропоновані учнями способи розв’язування не завжди раціональні, проте для навчальних і виховних цілей така робота дуже важлива: учні з великою зацікавленістю знаходяться у пошуках, перебираючи у пам’яті варіанти використання вивчених теорем, відомих прийомів і методів розв’язування проблемних задач.

Розглянемо це на прикладі твердження «Діагоналі ромба перетинаються під прямим кутом», з яким учні вперше зустрічаються при вивченні теми «Ромб та його властивості»:

І спосіб доведення.

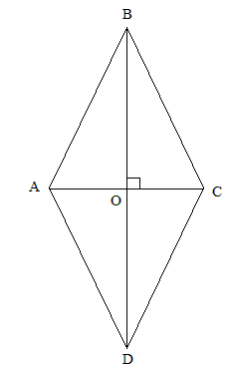Нехай діагоналі ромба ABCD перетинаються в точці О. Оскільки сторони ромба  рівні, то трикутник ABC рівнобедрений з основою АС. BO  медіана, бісектриса і висота ABC. Отже, діагоналі ромба перетинаються під прямим кутом.

Разом з тим, на уроці можна розглянути й інший спосіб доведення вказаної властивості ромба. Нехай ∠BAD = , ∠ABC= 180° — (сума будь-яких двох сусідніх кутів ромба рівна 180°). Діагоналі ромба є бісектрисами його кутів, бо ABO = BOC = DOC = AOD (за ІІІ ознакою рівності: AB=BC=CD=AD, як сторони ромба, AO = OC, BO = OD, діагоналі точкою перетину діляться навпіл).

Тобто ∠ BAО= ∠OAD = ; ∠АBO=∠BOC = = 90 -

Розглянемо ABО: Нехай ∠AOB = , тоді: + 90 - + = 180, (як сума внутрішніх кутів трикутника), = 90  отже, BD⊥AC, що і треба було довести.

Майже кожна задача з шкільного курсу математики допускає два чи кілька способів розв'язування.  Процес навчання розв’язувати геометричні задачі  різними способами дає вчителю можливість спонукати учнів до більш вдумливого вивчення геометрії, а учням більш повно дослідити властивості геометричних фігур чи одержати цікаве узагальнення задачі і т.д.

Керівна роль вчителя під час пошуку інших варіантів розв’язування проблемних задач дуже  важлива. Він сам повинен добре  розв’язувати задачі, знати наперед, скількома способами можна знайти відповідь у кожній з них, ефективно використовувати при цьому час уроку. Як правило, пошуки різних способів розв’язування дуже зацікавлюють учнів, особливо здібних до математики. Поки вчитель розв’язує задачу одним способом з рештою класу, здібні до математики діти вже встигають знайти кілька інших способів. Розв’язування задач різними способами веде до розвитку вмінь всебічно аналізувати задану задачу.

Ми пропонуємо декілька проблемних ситуацій, які можна створити на уроках алгебри і початків аналізу в 10-11 класах загальноосвітньої школи.

Наприклад, на уроці з теми «Тригонометричні рівняння та нерівності» (10-ий клас) корисно запропонувати учням усну контрольну роботу такого змісту. Розв’язати рівняння та нерівності:

1. 2cosx+4=0

2. sinx(cosx-6)=0

3. (1+tg2x) cos2x =0

4. cosx(2sinx-4)=0

5. sinx·(2cosx+1)=0

6. sin² x cos x ≥ 0

7. cos²x·sinx<0

9. cos x ≥

10. sin2 x <

Усне виконання подібних завдань сприяє вдосконаленню такої мислительної операції, як аналіз, і добре тренує пам’ять.

В 11-ому класі, при вивченні похідної функції y=cos x можна дати учням завдання знайти похідні наступних функцій у зазначеному порядку:

1) f(x)=sin2x;

2) g(x)=sin(2x+1);

3) t(x)=cosx.

Знаючи формулу похідної для y=sinx, учні легко виконують  перші завдання. А як знайти похідну для t(x)=cosx? Виникає пропозиція:  функцію  косинус  задати формулою, яка буде містити синус, наприклад,  cos x =  sin

При вивченні теми «Первісна функції»(11-ий клас), можна запропонувати учням виконати таке проблемне завдання.

1. Знайти похідні функцій:

1. y = 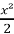;   2) y =  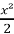 + 10;  3) y =  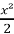  6

Виконавши це завдання, учні встановлюють, що для усіх випадків y'=x. Виникає проблема: для яких ще функцій y їх похідна рівна x? Виявляється, що  таких функцій безліч. А як зручніше записати відповідь? Напевне, у вигляді:

y = , де с=сonst.

Нарешті, розв’язуємо основну проблему: якщо F(x)  первісна для f(x) на деякому проміжку, то чи завжди F(x)+c теж є первісною на цьому самому проміжку?

2. При вивченні теми «Первісна суми функцій» ми пропонуємо завдання знайти первісні таких функцій:

1) f(x)=x3; 2) g(x)=sinx; 3) h (x)=x3+sinx.

Легко розв’язавши перші два завдання, для третього учні висувають припущення, що однією з первісних може бути така:

H (x) + cos x

Це можна обґрунтувати подальшою перевіркою гіпотези. Дійсно, якщо h(x)=f(x)+g(x), то можна записати H(x)=F(x)+G(x), де F'(x)=f(x), G'(x)=g(x). Доводиться ця формула безпосереднім застосуванням означення первісної.

Отже, застосування проблемного методу навчання на уроках математики привчає учнів: творчо мислити; самостійно висувати та перевіряти гіпотези; раціонально планувати пошук розв'язування задачі; порівнювати та аналізувати отримані результати; пізнавати основні методи розв'язування задач тощо.

 

2.2. Методичні вимоги й рекомендації щодо організації проблемного навчання уроках математики

 

Відомо, що при вивченні математики учні повинні засвоювати не лише зміст знань, а й способи їх отримання. Ефективним засобом активізації пізнавальної діяльності учнів є проблемний підхід до навчання. Він сприяє інтелектуальному розвитку учнів і водночас формує моральні та емоційні риси особистості.

Проблемно-пошукове навчання зближує процес навчання в школі з науковим пізнанням, розвиває творче мислення.

Для створення проблемної ситуації на уроці потрібно виконати ряд умов.

1. Проблемне завдання, на основі якого створюється проблемна ситуація, повинно ґрунтуватися на тих знаннях і вміннях, якими володіють учні, тобто, щоб зміст був доступний для них, тому завдання має випливати із змісту матеріалу, який вивчається, бути логічно пов’язаним з ним.  Необхідно зазначити, що уміння бачити проблему там, де вона є, не менш важливе від уміння її вирішити. До того ж, розв'язання проблем, виявлених самими учнями, відбувається на вищому рівні розумової активності.

2. Виконання проблемного завдання має викликати в учнів потребу в нових знаннях чи способах дії. Спостереження показують, що без врахування інтересів і потреб учнів, організовувати проблемне навчання неможливо. Навіть ідеальні проблемні завдання не утворять проблемної ситуації, якщо учень поставиться до них байдуже. Тому кожне заплановане проблемне завдання необхідно проаналізувати як з інформаційного, так і з мотиваційного боку.

3. Проблемні завдання, які вчитель планує розв’язати на уроці, мають бути узагальнюючими. Перехід від однієї проблемної ситуації до наступної, яка містить нові знання чи спосіб дії, повинен передбачати забезпечення подальшого розвитку дій і мислення учнів.

4. Важливою умовою успішного створення проблемних ситуацій є правильне і вміле формулювання проблемного завдання. Формулюючи проблемні завдання, не слід вживати слів, зміст яких учні розуміють погано.

На цьому етапі висувають гіпотези щодо шляхів розв'язання сформульованої проблеми. Як відомо, гіпотеза – це своєрідна стратегія вирішення проблеми. Її створення можливе тільки тоді, коли учні дуже глибоко вникнуть у суть самої проблеми, усвідомлять її глибину.

Загалом, у ході  уроку  учні разом з учителем можуть висунути декілька гіпотез вирішення поставленої проблеми. Кожну з гіпотез треба перевірити.

Отже, наступний етап технології проблемного вивчення матеріалу –перевірка висунутих гіпотез. Перевірка висунутих гіпотез передбачає залучення учнів до активної розумової діяльності. Вона відбувається з допомогою учителя. Якщо декілька учнів висунули гіпотези, то виникає потреба сформувати групи, які б займалися перевіркою кожної гіпотези. Необхідно вислухати  кожну групу, знайти в міркуваннях помилку, якщо вона є.

На етапі аналізу отриманих результатів і перевірки гіпотез, учитель разом з учнями відбирає ту гіпотезу, яка доведена без жодної наукової помилки. Їх може бути декілька. Але якщо вони правильно доведені, то повинні привести до однакового результату. Критерієм відбору гіпотез є, звичайно, практика. Треба намагатися одержаний результат перевірити будь-яким практичним способом.

Висновок і узагальнення як елемент методу і технології не є, однак, остаточною ланкою в ланцюгу міркувань, хоч і виділяє ті знання, які нарешті отримали учні. Остаточну крапку ставить повернення до проблемної ситуації. Коли знову повертаємося до проблемної ситуації, то з погляду отриманих знань з'ясовуємо, а чому, власне, виникла ця ситуація, і даємо їй пояснення.

Аналізуючи всю послідовність  етапів проблемної  технології, бачимо, що  самі знання учні отримують ніби то як побічний продукт, адже головна  увага  була приділена власне  розв'язанню  проблеми, тобто  шляху одержання цих знань, методу їх здобування. У тому і цінність проблемного вивчення матеріалу, оскільки нові знання учень отримує не в готовій формі, а внаслідок розумової праці, вони є його власним відкриттям, продуктом розумової діяльності.

Варто зазначити, що застосування проблемного методу під час вивчення математики у розумовому розвитку учнів принесе безумовну користь тільки тоді, коли воно буде підпорядковано чіткій системі роботи вчителя з використання активних методів навчання.

На основі аналізу літературних джерел, узагальнення власного досвіду роботи ми пропонуємо такі рекомендації по створенню проблемних ситуацій на уроках математики:

• щоб створити проблемну ситуацію, перед учнями варто поставити таке практичне або теоретичне завдання, виконання якого вимагає відкриття нових знань і оволодіння новими вміннями; тут може йти мова про загальну закономірність, загальний спосіб діяльності або загальні умови реалізації діяльності;
• завдання повинне відповідати інтелектуальним можливостям учня; ступінь труднощів проблемного завдання залежить від рівня новизни матеріалу викладання й від ступеня його узагальнення;
• проблемне завдання дається до пояснення засвоюваного матеріалу;
• проблемними завданнями можуть бути: засвоєння, формулювання питання, практичні завдання; проблемне завдання може привести до проблемної ситуації тільки у випадку урахування вищезгаданих правил;
• та сама проблемна ситуація може бути викликана різними типами завдань;
• дуже важку проблемну ситуацію вчитель направляє шляхом вказівки учневі причин невиконання даного йому практичного завдання або неможливості пояснення їм тих або інших фактів.

Отже, перш ніж створювати проблемну ситуацію на уроці, необхідно здійснити спеціальну підготовчу роботу, спрямовану на активізацію пізнавальної діяльності учнів. Створюючи проблемну ситуацію, вчитель збуджує найважливішу рушійну силу розумової активності – перехід від досягнутого рівня знань і розумового розвитку до нової сходинки, на яку треба піднятися в процесі оволодіння новими знаннями.

ВИСНОВКИ

 

В умовах сьогодення перед школою ставиться завдання формування всебічно розвиненої особистості, яка спроможна думати в нестандартних ситуаціях, досягнення високої якості засвоєння знань та розвиток здібностей школярів до самоосвіти. Реалізація цих завдань можлива за умов впровадження у навчальний процес технології розвиваючої освіти, яка спрямована на активне одержання учнями знань, формування прийомів дослідницької пізнавальної діяльності, залучення до наукового пошуку, творчості, виховання соціально вагомих рис особистості. Цьому сприятиме використання проблемних ситуацій на уроках математики, як основного методу проблемного навчання, який стимулює навчальний процес і підвищує загальну пізнавальну активність учнів на уроці.

Взагалі, проблемне навчання  це тип розвиваючого навчання, при якому поєднуються систематична самостійна пошукова діяльність учнів із засвоєнням ними готових висновків науки, а система методів побудована з урахуванням цілеспрямованості та  принципу проблемності. Воно орієнтується на формування пізнавальної самостійності, стійких мотивів засвоєння знань і розвитку розумових здібностей учнів та визначається системою проблемних ситуацій.

Проведено порівняльну характеристику традиційного і проблемного навчання. Зроблено висновок, що впровадження у навчальний процес з математики проблемного навчання, порівняно із так званою «пасивною» моделлю має ряд переваг: учні  засвоюють усі рівні пізнання (знання, розуміння, застосування, аналіз, синтез, оцінку); відсоток засвоєння, як правило, високий; педагог сильніше розкривається перед учнями як особистість, виступає як лідер, організатор; роль учнів активна, вони приймають важливе рішення стосовно процесу навчання; джерело мотивації  внутрішнє (інтерес самого учня).

Сутність проблемного навчання полягає в створенні (організації) перед учнями проблемних ситуацій, усвідомленні, прийняті та вирішенні цих ситуацій в процесі спільної діяльності учнів та учителя. Але такі ситуації не виникають самі, а стають результатом дидактичної майстерності педагога.

Основною категорією проблемного навчання є проблемна ситуація, для оволодіння якою учень або колектив мають знайти й застосувати нові для себе знання чи способи дій.

Проблемна ситуація в навчанні математики – це пізнавальна трудність, для подолання якої учні мають здобути нові знання або докласти інтелектуальних зусиль. Проблемний метод трансформує в собі концентрацію набутих знань та аналітичний пошук нового способу розв’язання поставленої проблеми.

Наведено способи створення проблемних ситуацій на уроках математики: підведення учнів до обґрунтування неочевидних залежностей, пропедевтичні завдання, підведення учнів до самостійних індуктивних висновків, розв’язання підготовчих вправ та задач, створення ситуації вибору, підведення учнів до висновків, що суперечать їх попереднім уявленням, організація дискусії, порівняння нового поняття з вивченим раніше.

Наведено приклади застосування проблемного  методу на уроках математики в середній школі. Проблемні запитання (ситуації) можуть виникати під час розв’язування нестандартної задачі, що потребує творчого підходу. Проблемне навчання на уроках математики  можливо застосовувати для засвоєння  узагальнених знань – понять, правил, законів, причинно-наслідкових та інших логічних залежностей

Окреслено умови й рекомендації для організації проблемного навчання на уроках математики. Важливим фактором, який допомагає правильно створити проблемну ситуацію на уроці математики, на думку вченого, було належне формулювання питання вчителем, а також формування в учня вміння аналізувати й систематизувати  зміст  проблеми. 

СПИСОК  ВИКОРИСТАНИХ  ДЖЕРЕЛ

 

1. Бриштан Т. Проблемне навчання на уроках математики / Т.Бриштан // Газета «Математика».  2007.  № 13. – С. 20-22
2. Гончарова  М. А. Проблемное  обучение  на  уроках  математики / М. А. Гончарова // Шк. технології. – 2013. – №2. – С. 96-105.
3. Дичківська І. М. Інноваційні педагогічні технології : навч. посіб. / І.М. Дичківська.  К. : Академвидав, 2004.  352 с.
4. Зеленська О. П. Взаємозв’язок проблемного навчання, мислення та мови / О. П. Зеленська // Педагогічний альманах.  2017.  Вип. 33.  С. 26-30
5. Коваленко В. Г. Проблемний підхід до навчання математики : методичний посібник / В. Г. Коваленко, І. Ф. Тесленко. – Київ: Радянська школа, 1985. – 88 с.
6. Ковальчук В. Реалізація технології проблемного навчання у процесі вивчення математики у початковій школі  / В. Ковальчук, Л. Силюга, Н. Стасів, Л. Білецька // Молодь і ринок.  2016.  № 7.  С. 6-10.
7. Мироновська Л. Розвивальний компонент технології проблемного навчання математики в початкових класах / Лариса Мироновська // Початкова шк. – 2012. – № 6. – С. 44–46.
8. Мордовец Т. Технология  проблемного  обучения / Т. Мордовец // Учитель. – 2012. – № 3. – С. 37–41.
9. Петрук Л. П.  Становлення і розвиток проблемного навчання у педагогіці  / Л. П. Петрук // Оновлення змісту, форм та методів навчання і виховання в закладах освіти.  2014.  Вип. 8.  С. 15-18.
10. Пінський І. В. Ігрові та проблемні ситуації на уроках математики : [геометрія, 7–8 кл. ; алгебра, 9–10 кл.] / І. В. Пінський // Математика (Шкільний світ). – 2004. – № 27–28  – С. 37–43.
11. Розвиток творчих здібностей у процесі навчання математики: зб. метод. матеріалів / [Г. В. Мовчан та ін. ; уклад. Т. В. Свєтлова]. - Харків : Основа, 2019. – 91 с.
12. Руденко О. Проблемна гра «Як поліпшити навчання математики» / О. Руденко // Розвиток  особистості  на  уроках  математики. / О. Руденко. – Київ, 2009. – С. 118–124.
13. Созанська О. Проблемне навчання – основа розвитку творчого мислення учня / О. Созанська // Заст. директора шк. – 2013. – № 8. – С. 30–39.
14. Теслюк В. М. Сутність та особливості проблемного навчання / В. М. Теслюк, І. І. Марійко // Вісник Національного університету оборони України.  2012.  Вип. 6.  С. 167-170.
15. Топузов О. Проблемна ситуація в теорії проблемного навчання / Топузов О. // Шлях освіти. – 2007. – №1. – 78 с.
16. Фіцула М. М. Педагогіка : навч. посіб. / М.М. Фіцула. — К. : Академія, 2001.  528 с.
17. Фурман А. В. Теорія навчальних проблемних ситуацій: психолого-дидактичний аспект.   Т. : Астон, 2007.  164 с.
18. Ягупов В. В. Педагогіка : навч. посіб. / В. В. Ягупов.  К. : Либідь, 2002. – 560 с.
19. Ямкова Л. І. Проблемний метод на уроці / Л.І.Ямкова // Математика в школах України.  2010 р.  № 30. – С. 18-19
20. Янц Н.Д. Класифікація проблемних ситуацій як напрям наукових пошуків // Засоби навчальної та науково-дослідної роботи: Зб. наук. пр. – Харків: Харківський національний педагогічний університет імені Г.С.Сковороди, 2008. – Вип.27. – С.149-155

 

ДОДАТОК

 

РОЗВ’ЯЗУВАННЯ  ПРОБЛЕМНИХ  ЗАВДАНЬ З  МАТЕМАТИКИ

В 5-6 КЛАСАХ

 

Задача 1: На запитання, скiльки важить рибина, рибалка вiдповiв: «Хвiст важить 150 г, голова стiльки, скiльки хвiст i половина тулуба, а тулуб – скiльки голова i  хвiст разом». Скiльки  важить цiла рибина?

Розв’язання:  Вага голови дорiвнює вазi хвоста плюс (+) половина ваги тулуба. Із умови задачi виходить, що вага тулуба дорівнює вазi хвоста плюс (+) половина ваги тулуба, плюс (+) вага хвоста. Значить половина  ваги  тулуба дорiвнює вазi  двох  хвостiв, тобто 150 х 2 = 300 г, а весь тулуб важить 600 г i тодi вага голови дорiвнює: 150 + 300 + 450 г. Тодi вага риби дорiвнює: 450 + 600 + 150 = 1200 г = 1кг 200г.

Задача 2: В Аравії  помирав  старий чоловiк. Все своє майно, 17 верблюдiв, він заповiдав  синам, причому старший мав одержати  половину, середнiй  третину а найменший  дев’яту частину. Пiсля смертi батька сини не знали, що  робити, бо 17 не дiлилося без остачi нi на 2, нi на 3, нi на 9. Довго сперечалися брати, аж тут пiд’їхав до них на верблюдi мудрець. Довiдався про суперечку i дав братам мудру пораду, яка й допомогла роздiлити майно так, як заповiв батько. Що то була за порада?

Розв’язання: Мудрець вiддав братам свого верблюда, верблюдiв стало 18. Тодi  їх  подiлили вiдповiдно до батькового заповiту. Старший одержав 9, середнiй 6, молодший 2. Усього 17. А мудрець забрав свого верблюда й поїхав далi.

Задача 3: По вулицi йшла дiвчинка. Зустрiвши дiдуся, вона привiталась. Дiдусь сказав: «Добрий день, маленька  дiвчинко!» Дiвчинка  заперечила, що вона не маленька, i коли дiдусь запитав скiльки їй рокiв, то вона вiдповiла: «в 2 рази молодша мами, а мама на 5 рокiв молодша батька. Разом нам 60 рокiв». Скiльки рокiв дiвчинцi?

Розв’язання: Роки дiвчинки приймемо за 1 частину, тодi роки мами складуть двi частини, а батька  двi частини + 5 рокiв. І так, п’ять частин складають 55 рокiв, а на одну частину припадае 55 : 5 = 11 рокiв.

Задача 4:  В недiлю рибалка ловив рибу 3 рази: вранцi, вдень i ввечерi.

Весь улов  3кг, причому, вранцi вiн зловив в 3 рази бiльше, нiж увечерi, а вдень стiльки ж, скiльки і ввечерi. Скiльки риби зловив рибалка вранцi i ввечерi?

Розв’язання: Вилов риби ввечерi  одна частина, вранцi  три частини, а вдень  одна частина. Отже, весь улов складає 1 + 3 + 1 = 5 частин; 3кг = 5 частин, тодi на одну частину припадає 3000 : 5 = 600г (це вечiрнiй улов), 600 х 1800г (ранiшнiй улов).

Задача 5:  Сашко витрачає на дорогу в школу 12 хвилин, а Марiйка 18 хв. Через 3 хвилини пiсля  виходу  Марiйки до школи  вийшов Сашко. Через який час вiн її наздожене?

Розв’язання: На пiв шляху. Оскiльки Марiйка витрачає на дорогу в школу в пiвтора рази бiльше часу, нiж Сашко, то через 6 хвилин Сашко її наздожене, пройшовши половину шляху, а Марiйка за той самий час також пройде  половину всього шляху.

Задача 6: Ставок заростає лататтям. Площа, яку покриває латаття, з кожним днем подвоюється. На десятий день заросла половина ставку. Яка частина ставку заросла на дев’ятий день?

Розв’язання: Оскільки площа, яку покриває латаття збільшується щоденно вдвічі і на десятий день заросла половини ставка, то на дев’ятий день заросла половина половини ставка, тобто четверта його частина.

Задача 7: На уроках домоведення  дiвчатка навчились пiдсмажувати шматочки хлiба. Пiдсмаживши одну сторону шматочка, на що йде 2 хв., його перевертають на другу сторону i смажать ще 2 хв. Сестра вирiшила  пригостити нас 3 шматочками, але на сковорiдку можна покласти тiльки 2 шматочки. Але вона не розгубилась і пiдсмажила 3 шматочки за 6 хв. Яким чином вона це зробила?

Розв’язання: Через 2 хв. дiвчинка перевернула один шматочок, а на мiсце другого поклала  третiй  шматочок. Через 4 хвилини перший шматочок  зняла, третiй перевернула i поклала на другу сторону другий шматочок.

Задача 8: Маємо три купи каменів: у першій  10, у другій  15, у третій – 20. За хід  дозволяється  розділити будь-яку купу на дві менші; програє  той, хто не може зробити хід. Який гравець виграє в цій грі?

Розв’язання: Наприкінці гри коли не можна зробити хід, маємо 45 куп по одному каменю. За будь-який хід куп збільшується на одиницю, тому вся гра має тривати точно 453=42 ходи. Отже другий гравець завжди виграє.