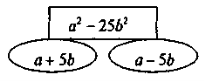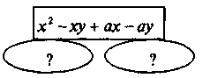Застосування різних способів розкладання многочленів на множники

Тема. Застосування різних способів розкладання многочленів на множники

Мета: систематизувати та узагальнити знання та вміння учнів щодо різних способів розкладання многочленів на множники; виробити вміння застосовувати різні способи розкладання многочленів на множники.

Тип уроку: систематизація та узагальнення знань.

Хід уроку

I. Організаційний момент

 Учитель:

1. перевіряє готовність учнів до уроку;
2. повідомляє оцінки за тематичну контрольну роботу № 5;
3. відповідає на питання стосовно завдань тематичної контрольної ро­боти, що виникли в учнів.

II. Перевірка домашнього завдання

Робота з випереджальним домашнім завданням.

Запитання до класу

1) Що називається розкладанням многочлена на множники?

2) Яку властивість множення  використовують під час винесення спільного множника за дужки?

3) В якій послідовності виконується розкладання многочленів на множ­ники способом групування?

4) Які алгоритми використовують під час розкладання на множники многочленів виду а² – b²; a² ± 2ab + b²; а³ ± b³?

Після бесіди проводиться самостійна робота із заповнення таблиці

По закінченні цієї роботи — перевірка (презентація) з наступною ко­рекцією.

Щоб зробити необхідні висновки, спонукаємо учнів до порівняння отриманих коментарів, після чого — узагальнюємо висновки.

III. Формулювання мети й завдань уроку

 Основну мету трьох уроків, об'єднаних темою «Застосування різних способів розкладання многочленів на множники», можна сформу­лювати так: 1) узагальнити й систематизувати знання й уміння щодо застосування кожного з вивчених трьох способів розкладання многочленів на множники, опанувати способи дій щодо комплекс­ного застосування цих способів під час розкладання многочленів на множники; сформулювати (якщо це можливо) певний алгоритм дій у ході розв'язування такого виду завдань; 2) ознайомитись із спек­тром завдань, розв'язання яких передбачає застосування різних способів розкладання многочленів на множники; 3) вироблення стійких навичок застосування різних способів розкладання многочленів на множники та розв'язування відповідних завдань.

Завдання на урок можна визначити як першу частину загального на­вчального завдання з теми (див. вище).

IV. Засвоєння нових знань

Зрозуміло, що опанування знань щодо різних способів розкладання многочленів на множники та вмінь їх застосовувати на практиці є дуже важ­ливим для успішного вивчення багатьох наук. Тому, щоб допомогти зорієнту­ватись учневі в безмежному просторі різних виразів, що розкладаються на множники, ми будемо намагатись дати певний алгоритм, зауваживши, що він є приблизним, тобто як і будь-яке правило, він має кілька винятків.

 Якщо знання про різні способи розкладання многочленів на множ­ники й уміння застосовувати ці знання на практиці в учнів на даний момент вироблені, єдине, що залишається вчителю — це разом з уч­нями спробувати сформулювати єдиний алгоритм виконання дій (послідовність застосування вивчених способів) під час розкладан­ня многочленів на множники. Після вдало виконаної роботи з випе­реджальним домашнім завданням ця процедура не повинна викли­кати в учнів труднощів, і формулювання алгоритму є логічним завершенням виконаної роботи.

Кількість прикладів, розглянутих учителем, може бути іншою, але ав­тор навмисне взяв саме такі приклади, щоб переконати учнів у справед­ливості алгоритму. Бажано, щоб учні порівняли хід розв'язаних вправ і самі переконалися в цьому.

Також важливо звернути увагу на такий момент, щоб попередити по­милки, яких традиційно припускають учні під час розв'язування завдань з теми: розкладання многочлена на множники вважається закінченим, якщо він поданий у вигляді добутку або лінійних множників (степінь 1) або множники більш високого степеня далі жодним з відомих семиклас­никам способів не розкладаються. Цей момент також виділяємо під час пояснення.

V. Засвоєння вмінь

Виконання письмових вправ

 Нa уроці традиційно відпрацьовуємо застосування сформульовано­го алгоритму й розв'язуємо відповідно вправи на його застосування.

1. Розкладіть на множники:

1а. 1) 7а² – 7b²; 2) km² – kn²; 3) 9х² – 36; 4) 4а³ – 4а; 5) х⁴ – х²;

      6) са² – 9сb²; 7) 2а³ – 2b³; 8) 27с + b³с.

1б. 1) 3р² + 6рq + 3q²; 2) - b² + 2bс – с²; 3) 81 – 54b + 9b²;

      4) 2xb² + 8хb + 8х; 5) 9а³ + 6а² + а; 6) т – 10т² + 25т⁵.

1в. 1) 3тп + 24п – 9т – 72; 2) -4abc – 32bc – 12ac – 96c;

      3) 1,5а² – 0,5а²х + 1,5ах – 0,5ах²;  4) х²у²а – х²у² + 5аху – 5ху.

2. Розв'яжіть рівняння: 1) 8х² – 72 = 0; 2) 12х² – 3 = 0.
3. Розкладіть на множники, знайдіть значення виразу:

     1) 4х² – 4у², якщо х = 51, у = 49;  2) 5а² – 10аb + 5b², якщо а = 7,3, b = 2,3.

4* (додатково). Логічна вправа.

Вставте пропущені слова, числа, вирази чи рисунки:

VI. Підсумки уроку

Бліцтест

1. В якому випадку вказано правильне розкладання многочлена 25х² – 25у² на множники:

1) 25(х² – у²); 2) (5х – 5у)(5х + 5у); 3) 25(х – у)(х + у); 4) 25(х – у)² ?

2. Відновіть логічний ланцюжок (розставте вирази 1) — 4) у порядку, що відповідає логіці уроку):

1) 2у³(у – а + аb – bу);  2) 2у³(1 – b)(у – а);

3) 2y³(y(1 – b) – a(1 – b)); 4) 2y⁴ – 2y³a + 2y³ab – 2y⁴b.

Який крок ви б додали до утвореного ланцюжка?

VII. Домашнє завдання

Використовуючи теорію та практичні навички, здобуті на уроці, вико­найте завдання.

№ 1. Розкладіть на множники:

1) 14 – 14m²; 2) 3a – 3a³; 3) 7х⁵ – 7xy²; 4) 5x²y² – 45а²b²;

5) 3х² – 24ху + 48у²; 6) -3п⁴ – 12п³ – 12п²; 7) 2а³ + 54b⁶;

8) 3х³ – 3ху – 3х² + 3х²у;  9) 0,2х⁴ + 0,6х³у – 0,4х³ – 1,2х²у.

№ 2. Знайдіть значення виразу:

1) 3т² + 6тп + 3п², якщо т = 4,8, п = 5,2;  2) 10а² – 10b², якщо а = 69, b = 31.

№ 3 (випереджальне). У даних виразах (ланцюжках) виділіть групи одночленів, щоб вони утворили вираз, що є або повним квадратом дво­члена або різницею квадратів двох виразів:

1) х² – 2ху + у² – z²;  2) с² + 9 – 6с – k²;  3) т² + 2тп + п² – k²;

4) a² – 8a – b² + 16;  5) а² – b² + а + b;   6) 4х² + у – 2х – у²;  7) с² – b² + с – b.