Завдання для І (шкільного) етапу Всеукраїнської учнівської олімпіади з математики у 2019/2020 н.р.
Завдання для І (шкільного) етапу
Всеукраїнської учнівської олімпіади з математики у 2019/2020 н.р.
9 клас
1. Знайти всі тризначні числа, у яких друга цифра у чотири рази більша від першої, а сума всіх трьох цифр дорівнює 14. (7 балів)
2. При яких натуральних х вираз ![]() є квадратом натурального числа? (7 балів)
є квадратом натурального числа? (7 балів)
3. Рибалка спіймав велику кількість риби вагою 3,5 кг і 4,5 кг. Але його рюкзак вміщує не більше ніж 20 кг. Яку максимальну вагу риби він може взяти з собою? Відповідь обґрунтуйте. (7 балів)
4. В прямокутному трикутнику з катетами 3 і 4 см проведені висота прямого кута і медіана більшого з гострих кутів. У якому відношенні висота ділить медіану? (7 балів)
Ключі для І (шкільного) етапу
Всеукраїнської учнівської олімпіади з математики у 2019/2020 н.р.
9 клас
Критерії оцінювання
|
Бали |
Пояснення |
|
7 |
Повний правильний розв’язок . |
|
6 |
Правильний розв’язок , але є невеликі недоліки, які в цілому не впливають на розв’язок. |
|
5 |
Розв’язок у цілому правильний, але він має ряд помилок, або не розглядає окремих випадків, але може стати правильним після невеликих виправлень або уточнень. |
|
4 |
Правильно розглянутий один з двох існуючих випадків. |
|
3 |
Доведені додаткові твердження, які допомагають при розв’язанні задачі. |
|
2 |
Розглянуті окремі важливі випадки при відсутності розв’язку (або при неправильному розв’язку). |
|
1 |
Записана тільки одна відповідь і вона є правильною, але розв’язку немає. |
|
0 |
Розв’язок неправильний, просування відсутнє. Розв’язок відсутній і відповідь неправильна. |
1. Якщо перша цифра не менше ніж 3, то друга цифра – не менше ніж 12, що неможливо. Отже, перша цифра 1 або 2. А далі число будується згідно умови задачі.
Відповідь: 149; 284.
2. Нехай ![]() . Відомо, що
. Відомо, що ![]() – квадрат деякого цілого числа
– квадрат деякого цілого числа ![]() , меншого за t. Тоді отримуємо
, меншого за t. Тоді отримуємо ![]() . Числа
. Числа ![]() і
і ![]() – натуральні і перше число більше, ніж друге. Значить,
– натуральні і перше число більше, ніж друге. Значить, ![]() , а
, а ![]() . Розв’язавши цю систему, отримаємо
. Розв’язавши цю систему, отримаємо ![]() ,
, ![]() , що дає
, що дає ![]() .
.
Відповідь: при х=5.
3. В рюкзак можна вмістити 0, 1, 2, 3 або 4 штук риби вагою 4,5 кг (не більше, тому що ![]() Для кожного з цих варіантів залишок місткості рюкзака не ділиться націло на 3,5 і тільки у крайньому випадку можливо удасться упакувати
Для кожного з цих варіантів залишок місткості рюкзака не ділиться націло на 3,5 і тільки у крайньому випадку можливо удасться упакувати ![]() кг риби.
кг риби.
Відповідь: 19, 5 кг.
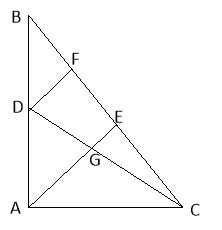 4. Проведемо відрізок DF паралельно висоті АЕ. За теоремою Фалеса він поділить відрізок BE навпіл. За теоремою Піфагора гіпотенуза трикутника АВС дорівнює 5 см. Крім цього
4. Проведемо відрізок DF паралельно висоті АЕ. За теоремою Фалеса він поділить відрізок BE навпіл. За теоремою Піфагора гіпотенуза трикутника АВС дорівнює 5 см. Крім цього ![]() і
і ![]() . Звідси маємо:
. Звідси маємо: ![]() ,
, ![]() . Тобто ВЕ=3,2, FE=1,6, EC=1,8. З паралельних відрізків DF і GE витікає, що
. Тобто ВЕ=3,2, FE=1,6, EC=1,8. З паралельних відрізків DF і GE витікає, що 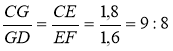
Відповідь: 9:8, починаючи від основи.


про публікацію авторської розробки
Додати розробку
