завдання для практичної роботи "Диференціальні рівняння"
ДИФЕРЕНЦІАЛЬНІ РІВНЯННЯ
Практичне заняття
Розв’язування диференціальних рівнянь з відокремлюваними змінними.
Мета. Засвоїти означення розв’язку диференціального рівняння та означення диференціального рівняння з відокремлюваними змінними, навчитись відокремлювати змінні та розв’язувати рівняння з відокремлюваними змінними.
Теоретичні відомості
|
Рівняння, які пов’язують незалежну змінну, невідому функцію і її похідні або диференціали різних порядків, називаються диференціальними рівняннями. Порядком диференціального рівняння називається порядок старшої похідної, що входить у це рівняння.
Функція Розв’язок диференціального рівняння, який містить скільки незалежних довільних сталих, що і порядок рівняння, називається загальним розв’язком цього рівняння.
Для знаходження частинного розв’язку диференціального рівняння задаються початкові умови. Для рівняння першого порядку вони мають вигляд За цими початковими умовами визначаються значення довільних сталих в загальному розв’язку рівняння, в результаті чого отримується частковий розв’язок, який задовольняє заданим початковим умовам. |
, яка задовольняє диференціальне рівняння, називається розв’язком цього рівняння. Графік розв’язку називається інтегральною кривою рівняння.
; для рівняння другого порядку 
.
Завдання 1
- Які з наступних рівнянь є диференціальними:
а) 
б) 
;
в) 
; г) 
д) 
; е) 
.
- Визначте порядок наступних диференціальних рівнянь:
а) 
б) 
в) 
; г) 
.
-
Визначте, яка з указаних функцій є загальним розв’язком диференціального рівняння
:
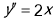а) 
;
б) 
;
в) 
;
г)
.
- Розв’язати рівняння:
а) 
б) 
в)
г) 
- Розв’язати рівняння:
а) 
б) 
в) 
Теоретичні відомості
Диференціальні рівняння з відокремлюваними змінними
|
Диференціальне рівняння з відокремлюваними змінними має вигляд
поділивши всі члени рівняння на N1(y) M2(x) - отримуємо рівняння
в якому змінні відокремлені. Загальний розв’язок рівняння знаходять почленним інтегруванням:
|
,
,
.
Завдання 2
Знайдіть загальний розв’язок диференціального рівняння:
а) 
б) 
в) 
г) 
д) 
Завдання 3
Знайти частковий розв’язок диференціального рівняння, який задовольняє вказаним початковим умовам:
а) 
б) 
в) 
г) 
Питання для самоконтролю
- Які основні поняття диференціального рівняння?
- Як розв’язати диференціальні рівняння з відокремлюваними змінними?
- Як розв’язати диференціальні рівняння першого порядку?
- Які основні формули лінійних диференціальних рівнянь І-го і ІІ-го порядків?
про публікацію авторської розробки
Додати розробку