Завдання І (шкільного) етапу олімпіади з математики

7 

Повне правильне розв’язання

6 -7

Повне правильне розв’язання. Є невеликі недоліки, які в цілому не впливають на розв’язання.

5 - 6

Розв’язання в цілому вірне. Однак воно містить ряд помилок, або не розглянуті окремі випадки, але може стати правильним після невеликих виправлень або доповнень.

4 - 5

Правильно розглянуто один з двох (більш складний) істотних випадків, або в задачі типу «оцінка-приклад» вірно отримана оцінка.

2 - 3

Доведені допоміжні твердження, що допомагають у розв’язанні задачі

1

Розглянуто окремі важливі випадки за відсутності розв’язання (або при помилковому розв’язанні).

0

Розв’язання неправильне, просування відсутні. Розв’язання відсутнє.

Розставте між числами довільні арифметичні дії (без повторень знаків дій)  так, щоб виконувалась рівність:     6   3   3 = 6  3   3

7б

Дано числа: 1, 2, 3, 4, 5, 6, 7, 8, 9. Розташуйте їх по чотири на кожній стороні трикутника так, щоб суми на кожній стороні трикутника були рівними  одному і тому ж  непарному числу.

7б

Віз сіна кінь з’їдає  за  місяць, коза – за два, а вівця – за три місяці. За який час кінь, коза і вівця з’їдять віз сіна?

7б

В одному дворі живуть четверо юнаків. Відомо, що Вадим і водій старші за Сергія, Микола і сантехнік захоплюються плаванням, бібліотекар – молодший із юнаків. Антон і перукар грають в доміно проти Сергія і бібліотекаря. Визначити професії юнаків.

7б

Скільки кроликів і курей знаходяться у клітці, якщо всього голів 35, а ніг  – 94?

7б

Розставити знаки „+” або „ - „ (усього не більше 4-х знаків) між

цифрами 987654321 таким чином, щоб цей вираз дорівнював 100.

7б

Батьки дали дітям на атракціони 24 гривні, які слід було розділити порівну. Але до них при­єдналися дві подруги, і гроші розділили порівну  між усіма. При цьому кожний одержав на 1 грн. менше, ніж передбачалося раніше. Скільки усього стало дітей?

7б

Щоб піднятися на третій поверх будинку, треба пройти 48 сходинок. Скільки сходинок треба подолати, щоб піднятися на шостий поверх, якщо кількість сходинок між поверхами однакова?

7б

Онуку стільки місяців, скільки років дідусеві.  Дідусь з онуком мають разом 91 рік. Скільки років дідусеві і скільки років онуку?

7б

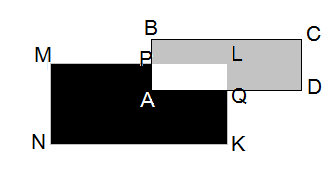
Прямокутники ABCD та KLMN зі сторонами  AB=3см , BC=5 см ,  MN=4см та ML=6см розташовані, як це показано на рисунку. Відомо, що площа сірої частини  прямокутника ABCD дорівнює 10 см². Визначте, чому дорівнює площа чорної частини

прямокутника KLMN.

7б

Кішка з кошеням з’їдають , куплений господарем, корм за 8 днів. Якби кішку годували одну, то їй вистачило б корму на 11 днів. На скільки повних днів вистачило б корму кошеняті ?

7б

Напис на надгробку  видатного математика Діофанта в м. Ісковії був зроблений у формі задачі.  Розв’яжи її, щоб  дізнатися

скільки років прожив Діофант.

Прах Діофанта гробниця ховає, вдивися – і камінь

Мудрим мистецтвом розкриє покійного вік:

З волі богів шосту частину життя був він дитина,

А ще половину шостої – стрів із пушком на щоках.

Тільки минула сьома, з коханою він одружився.

З нею п’ять років проживши, сина діждався мудрець.

Та півжиття свого тішився батько лиш сином.

Рано могила дитину у батька забрала.

Років двічі по два батько оплакував сина.

А по роках цих і сам стрів він кінець свій печальний.

7б

У двох кошиках було 120 яблук. Після того як з одного кошика вийняли 28 яблук, у кошиках залишилося яблук порівну. Скільки яблук було у кожному кошику спочатку?

7б

На уроці математики Тарас записав деяке число. Потім він поділив його на 7 і додав 7, а потім отриманий результат помножив на 7. У відповіді отримав 777. Яке число Тарас записав спочатку ?

7б

У ромбі ABCD проведено бісектрису ВМ кута АВD, яка утворює зі стороною ромба АD кут 120º. Знайдіть кути ромба.

7б

Якщо день народження учня помножити на 12, а номер місяця на 31, то сума отриманих добутків дорівнює 170. Коли народився учень?

7б

В Афінах  була водойма з трьома трубами. Перша труба могла наповнити водойму за 1 годину, друга – за 2 години, а третя за 6 год. За який час усі три труби, працюючи разом, могли наповнити водойму?

7б

Кожного дня народження Оксана отримує в подарунок стільки квіток, скільки років їй виповнилося. Ці квіти засушуються і зберігаються у гербарії. Зараз в Оксани 120 квіток. Скільки їй років ?

7б

Побудувати графік функції: 

у =

7б

ин Один з кутів рівнобедреного трикутника дорівнює 120 .

З З середини основи опущено перпендикуляр на бічну сторону. В якомякому відношенні основа перпендикуляра ділить бічну сторону?

7б