Завдання олімпіади "Шкільний етап"

 

Шкільний етап Всеукраїнської  учнівської олімпіади з математики

2022–2023 н. р.

Завдання

6 клас

1. Відновіть ребус КОКА+ КОЛА = ВОДА (однаковим буквам відповідають однакові цифри, різним буквам - різні цифри). (7б)

2. Зафарбуйте деякі клітинки так, щоб на полі було розташовано класичний набір корабликів (чотири 1×1, три 2×1, два 3×1 і один 4×1) і частини різних корабликів не розташовувалися в сусідніх по стороні чи вершині клітинках. (7б)

3. На алеї від будинку до озера росте 17 дерев. Юрко, ідучи з дому до озера, відмітив крейдою перше дерево, а потім кожне друге дерево. На зворотному шляху до будинку він знову відмітив перше дерево (від озера), а потім кожне третє дерево. Скільки дерев залишилось невідміченими? (7б)

 

4. . Яблука зимових сортів становили 45% від усієї  кількості зібраних фруктів у саду, а яблука сорту «Чемпіон» становили 40% від загальної кількості зібраних яблук. Скільки центнерів фруктів було зібрано, якщо яблук сорту «Чемпіон» зібрали 10,8 ц? (7б)

 

 

5. Фігури 1, 2, 3, 4, 5 – квадрати. Периметр квадрата 1 дорівнює 12 см.  Знайдіть периметр квадрата 5. (7б)

 

1	1	3	5
2
4

 

 

 

Шкільний етап Всеукраїнської  учнівської олімпіади з математики

2022–2023 н. р.

Завдання

7 клас

1. Відновіть ребус КОКА+ КОЛА = ВОДА (однаковим буквам відповідають однакові цифри, різним буквам - різні цифри). (7б)

2. Чи ділиться на 6 число 10²⁰¹⁷+2016? Відповідь обґрунтуйте. (7 б)

 

3. Знайдіть цілі числа і такі, що . (7 б)

 

4. Як розділити на дві рівні частини 12 відер хлібного квасу, налитого у 12-відерну бочку, користуючись 8-відерною та 5-відерною порожніми бочками? (7 б)

 

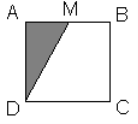5. У квадраті АВСD точка М є серединою відрізка АВ. Знайдіть площу квадрата АВСD, якщо площа затемненої частини дорівнює 7 см²? (7 б)

 

 

 

Шкільний етап Всеукраїнської  учнівської олімпіади з математики

2022–2023 н. р.

Завдання

8 клас

1. Довести, що сума    ділиться на 120. (7 б)

2. На яку цифру закінчується число 1999²⁰²²? (7 б)

3. Знайдіть значення виразу  , якщо      (7б)

4. Василь задумав три різні ненульові цифри. Петро записав всі дев'ять можливих двозначних чисел, у десятковому записі яких використовувалися тільки ці цифри (з повторенням). Сума записаних чисел дорівнює 231. Знайдіть цифри, задумані Василем. (7 б)

5.У трикутнику ABC бісектриса з вершини A, висота з вершини B та серединний перпендикуляр до сторони AB перетинаються в одній точці. Знайдіть величину кута A. (7 б)

 

 

 

 

 

 

 

 

 

 

 

Шкільний етап Всеукраїнської  учнівської олімпіади з математики

2022–2023 н. р.

Завдання

9 клас

1. Для нумерації сторінок задачника знадобилося 1224 цифри. Скільки сторінок у книзі?    Нумерація починається з першої сторінки. (7 б)

2. Знайти усі цілі додатні числа x, y, z  які задовольняють рівність

(7 б)

3. У Петрика було 4 аркуші паперу. Деякі із них він розрізав на 8 частин, після чого деякі знову розрізав на 8 частин і т. д. Після чергового розрізання він підрахував кількість аркушів і з'ясував, що їх 2022. Чи правильний підрахунок зробив Петро? Відповідь пояснити. (7 б)

4. Андрій та Матвій грають у гру. На дошці записуються числа 63 та 55. За один хід дозволяється записати ще одне число, що є різницею двох чисел, які вже записані. Числа на дошці не повинні повторюватись. Програє той, хто не може зробити хід. Андрій починає першим. Хто виграє, Андрій чи Матвій? (7 б)

5. У трикутнику АВС бісектриса, яка проведена з вершини А, висота з вершини В і серединний перпендикуляр до сторони АВ перетинаються в одній точці. Знайдіть величину кута А. (7 б)

 

Шкільний етап Всеукраїнської  учнівської олімпіади з математики

2022–2023 н. р.

Завдання

10 клас

1. Заповніть клітинки таблиці так, щоб числа в кожному рядку і в кожному стовпці утворювали геометричну прогресію:

27
		36
	6
			8

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2. Визначте останню цифру числа 43⁴³ – 17¹⁷.

 

3. Довести, що якщо 4х + 3у ділиться на 5, то і 2х – у також ділиться на 5.

 

4. Футбольні матчі між командами «Зубило», «Дробило», «Молотило» виявилися дуже результативними. Команда «Зубило» в сумі забила 60 голів, «Дробило» пропустила 80, «Молотило» забила стільки ж голів, скільки ж і пропустила. Доведіть, що в матчі «Дробило»-«Молотило» було забито не менше 40 голів.

 

5. Центр Р кола, описаного навколо опуклого чотирикутника ABCD, лежить в середині цього чотирикутника. При цьому діагоналі чотирикутника перпендикулярні, а сторони AB і CD не паралельні. Доведіть, що площі трикутників АВР  і CPD рівні.

 

 

 

Кожне завдання оцінюється в 7 балів.

Користування калькулятором заборонено.

 

 

 

 

 

 

 

 

 

Шкільний етап Всеукраїнської  учнівської олімпіади з математики

2022–2023 н. р.

Завдання

11 клас

1. Довести, що , якщо , ,

 .

2. Розв'яжіть систему:

3.  Було 6 аркушів паперу. Деякі з них розрізали на 6 частин, потім деякі знову розрізали на 6 частин. Коли підрахували загальну кількість аркушів, то виявилося, що їх було 2022. Чи правильно виконано підрахунок?

 

4. Березовий гай має форму круга радіуса 215 м. Відстань між деревами у цьому гаю не менше 10 м. Доведіть, що в гаю дерев менше за 2022. Скільки максимально може бути дерев?

 

5. В трапецію вписано коло радіуса r. Знайдіть площу трапеції, якщо кути при більшій основі рівні α та β.

 

Кожне завдання оцінюється в 7 балів.

Користування калькулятором заборонено.