Шкільна математична олімпіада 9 клас

1. Розв’яжіть нерівність
2. Знайдіть область визначення функції
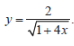
3. Яких і на якому місці слід закреслити 10 цифр числа 109379289456847510623, щоб отримати найбільш можливе число.
4. На відрізку AD позначено точки В і С так, що АВ = ВС -CD. Знайдіть координати точки D, якщо А(5; 2), В(3; 1).
5. Доведіть, що точки A, B і C лежать на одній прямій, якщо AB = 8,3 см, BC= 10,1 см, AC=l,8 см. Яка з цих точок лежить між двома іншими?

Шкільна математична олімпіада 10 клас

1. Між цифрами 7   9   2   3   4   8   6  розставити арифметичні знаки + та - так, щоб в результаті  вийшло число 15.
2. Встановити вид чотирикутника, в якому кожна діагональ розбиває його на два прямокутних трикутники. Відповідь поясніть.
3.  Знайдіть суму коренів рівняння (х-1)³=4(х-1)
4. На стороні  трикутника  QPR вибрали точку S так, що 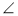QPS=12^o, QP=PS=RS . Знайдіть PRQ.
5. Обчислити значення виразу 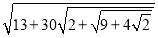. Відповідь округлити до цілих.

. В Шкільна математична олімпіада 11 клас

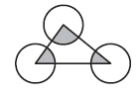
1. Центри кіл, радіус кожного з яких 2, не перетинаються і лежать у вершинах трикутника. Знайдіть суму площ заштрихованих фігур.
2. Чи може дискримінант квадратного рівняння ax²+bx+c=o з цілими коефіцієнтами дорівнювати 23?
3. Знайти величину (х + у)², якщо 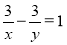та у – х = - 2.
4. Доведіть, що добуток трьох послідовних натуральних чисел, складений з другим із них, є кубом другого числа.
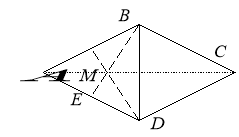5. Дві висоти ромба, проведені з вершин його тупих кутів, перетинаються та діляться у відношенні 1:2. Знайти  кути ромба.

Шкільна математична олімпіада 7 клас

1. Визначте периметр многокутника, зображеного на рисунку.

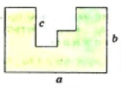
2. B одному мішку було 80 кг борошна, а в другому — 60 кг. Із першого мішка відсипали борошна в 3 рази більше, ніж з другого, і тоді в другому мішку борошна залишилося вдвічі більше, ніж у першому. Скільки кілограмів борошна взяли з кожного мішка?
3. У тотожності 5х+3х=8х замініть змінну х виразом а²-ас+с². Чи є тотожністю одержана рівність?

4. Чотири олівці і три зошити коштують 82 к., 2 олівці й 2 зошити - 50 к.. Скільки коштують: а) 8 олівців і 7 зошитів; б) 8 олівців та 4 зошити?
5. Скільки тасьми необхідно взяти для оздоблення абажура настільної лампи, який має форму кола діаметром 17,3 см?