Завдання з теми "Нерівності з параметрами"
У задачах, що описують реальні фізичні процеси, досить часто крім невідомих зустрічаються величини, які називаються параметрами. Їх, як правило, позначають літерами a, b, c, m, k, і т. д., а невідомі - x, y, z, і т. д. В основу розв’язання задач із параметрами покладено такий принцип: значення параметра (або параметрів) вважається довільно фіксованим і розв’язок задачі знаходитися традиційними методами. Проте наявність параметрів у задачі передбачає обов’язкове дослідження існування розв’язку залежно від конкретних числових значень параметрів із області їх допустимих значень, а також знаходження всіх таких розв’язків. Задачі з параметрами, таким чином, розглядаються як ціла множина рівнянь, нерівностей або їх систем, які отримуються, коли параметри набувають конкретних значень. Форма запису відповіді у задачах з параметрами має спеціальний вигляд: значення невідомих вказуються для кожного допустимого значення параметрів.
Для розв’язання задач з параметрами необхідні ґрунтовні знання властивостей елементарних функцій, рівносильних перетворень рівнянь та нерівностей.
Як було вказано вище, нерівності, які крім букв, що позначають невідомі, містять інші букви, які називаються параметрами. Фактично ми маємо справу не з однією нерівністю, а з нескінченною множиною нерівностей.
Значення параметрів, при яких вирази в лівій та правій частинах нерівності мають зміст, називаються допустимими.
Розв’язати нерівність з параметрами означає знайти всі її розв’язки для кожної системи допустимих значень параметрів. Значення параметрів, при переході через які відбуваються якісні зміни нерівності, називаються контрольними значеннями параметрів.
Нерівності виду ax >< b ,де a i b – дійсні числа, x - змінна, називаються лінійними нерівностями з однією змінною. Розв’язки нерівності суттєво змінюються в залежності від числа a; від умов
a = 0, або a < 0, або a > 0.
Приклад 1.
При будь-якому значенні m розв’язати нерівність
(m - 1) x < 5m
Розв’язання.
- Якщо m = 1, то 0x < 5, x є R,
-
Якщо m > 1, то x <
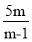
 ,
,
-
Якщо m < 1, то x >
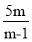 .
.
Відповідь: якщо m < 1, то x є (![]() ; + ∞);
; + ∞);
якщо m = 1, то x є R
якщо m > 1, то x є (- ∞ ; ![]() )
)
Приклад 2
При будь-якому значенні параметра а розв’язати нерівність:
![]() х –
х –![]() < 2x – 1
< 2x – 1
Розв’язання
О Д З а ≠ 1
(![]() -2)х <-
-2)х <-![]()
![]() х <-
х <-![]()
![]() х <-
х <-![]()
![]() х>
х>![]()
1)![]() = 0, тобто a = 4, маємо 0x >
= 0, тобто a = 4, маємо 0x >![]() ,хє
,хє![]() .
.
2) ![]() > 0, a є (- ∞ ; 1)
> 0, a є (- ∞ ; 1) ![]() (4 ; + ∞), маємо x >
(4 ; + ∞), маємо x >![]() .
.
3) ![]() < 0, a є (1 ; 4), маємо x <
< 0, a є (1 ; 4), маємо x < ![]() .
.
Відповідь: Якщо a = 1 або a = 4, то x є![]() ;
;
Якщо а є (- ∞ ; 1) ![]() (4 ; + ∞), то х є (
(4 ; + ∞), то х є (![]() ; + ∞ ) ;
; + ∞ ) ;
Якщо а є (1 ; 4), то х є ( - ∞;![]() ).
).
Приклад 3
При будь-якому значенні а розв’язати нерівність.
![]() -
-![]() <
<![]()
Розв’язання :
![]() -
-![]() <
<![]()
3(а2х+1) – 2(a2 x + 3) < a + 9x
3a2x - 2 a2x – 9x < 6 – 3 + a
(a2– 9)x < 3 + a
1) a2– 9 = 0, a = 3 aбо a = -3
Якщо a = 3,то 0x < 6, x є R;
Якщо a = -3, то 0x < 0, x є ![]() ;
;
2) a2– 9 > 0, (a - 3)(a + 3) > 0, a є (- ∞; -3) ![]() (3 ;+ ∞),
(3 ;+ ∞),
маємо x <![]() , x <
, x <![]() ;
;
3) a2– 9 < 0, (a - 3)(a + 3) < 0,aє(-3;3), маємо x >![]() .
.
Відповідь : Якщо a є (- ∞; -3) ![]() (3 ;+ ∞), то x є ( - ∞;
(3 ;+ ∞), то x є ( - ∞;![]() );
);
Якщо а є (-3; 3), то х є (![]() ; + ∞) ;
; + ∞) ;
Якщо a = -3, то х є![]() ;
;
Якщо a = 3, то х є R .
Приклад 4
При будь-якому значенні параметра а розв’язати нерівність.
![]() + a2 – 2 >
+ a2 – 2 > ![]() +
+ ![]() .
.
Розв’язання :
![]() + a2 – 2 >
+ a2 – 2 > ![]() +
+ ![]()
ax + 2a2 – 4 > a3 – 1 + 2a3 + x – 4
(a - 1)x > 3a3 - 2a2 - 1
Розкладемо 3a3 - 2a2 – 1 на множники:
3a3 - 2a2 – 1 = 2a3 - 2a2 + a3 – 1 = 2a2 (a – 1) + (a – 1)( a2 + a + 1) =
=(a - 1)(2a2 + a2+ a + 1) = (a - 1)( 3a2 + a + 1)
Нерівність приймає вигляд:
(a - 1)x > (a - 1)( 3a2 + a + 1)
-
Якщо а = 1, то 0x > 0, x є
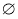 ;
;
- Якщо а > 1, то x > 3a2 + a + 1;
- Якщо а < 1, то x < 3a2 + a + 1.
Відповідь : Якщо а є (- ∞;1), то х є (- ∞; 3a2 + a + 1);
Якщо а = 1 , то х є![]() ;
;
Якщо а є (1; + ∞), то х є (3a2 + a + 1; + ∞).
Приклад 5
При будь-якому значенні параметра m розв’язати нерівність.
![]() -
-![]() >
>![]() Розв’язання:
Розв’язання:![]() -
-![]() >
>![]() О Д З m ≠ + 1
О Д З m ≠ + 1
![]() >
>![]()
![]() >
>![]()
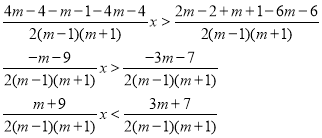
1) ![]() =0
=0
m=-9
маємо ох<-![]() , хє
, хє![]() .
.
2) ![]() >0; (m+9)(m-1)(m+1)>0
>0; (m+9)(m-1)(m+1)>0

mє (-9; -1) ![]() (1; + ∞)
(1; + ∞)
При таких значеннях m розв’язуємо дану нерівність:
x <![]()
x <![]()
3) ![]() <0
<0
(m+9)(m-1)(m+1)<0
mє(- ∞ ; -9) ![]() (-1; 1)
(-1; 1)
При таких m розв'язуємо дану нерівність.
x >![]()
x >![]() .
.
Відповідь:Якщо mє(- ∞ ;-9) ![]() (-1; 1),тохє (
(-1; 1),тохє (![]() ;+∞) ; якщо mє(-9;-1)
;+∞) ; якщо mє(-9;-1)![]() (1;+∞),тохє(- ∞;
(1;+∞),тохє(- ∞;![]() ) ; якщоm=-9;1;-1, то х є
) ; якщоm=-9;1;-1, то х є![]() .
.
Приклад 6
При будь-якому значенні параметра а розв’язати нерівність.
![]()
Розв’язання
![]()
О Д З а ≠ 2
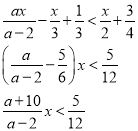 ;
;
1) а=-10; 0х<![]() , хєR.
, хєR.
2) ![]() >0, (a + 10) . (a - 2) > 0
>0, (a + 10) . (a - 2) > 0
a є (- ∞; - 10) ![]() (2; + ∞)
(2; + ∞)
x < ![]()
3) ![]() < 0 , (a + 10) . (a - 2) < 0
< 0 , (a + 10) . (a - 2) < 0
a є (- 10; 2)
x > ![]()
Відповідь: якщо a є (- ∞; - 10) ![]() (2; + ∞), то х є (- ∞ ;
(2; + ∞), то х є (- ∞ ; ![]() );
);
якщо a є (- 10; 2) , то х є (![]() ; + ∞);
; + ∞);
якщо а = - 10, то х є R;
якщо а = 2, то х є ![]() .
.
Приклад 7
При будь-якому значенні параметра а розв’язати нерівність.
![]()
Розв’язання
![]()
О Д З а ≠ + 1
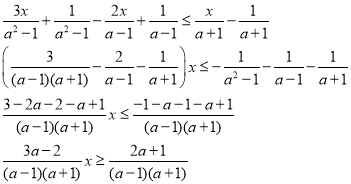
-
3a – 2 = 0; а =
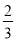
0х ≥ -![]() , х є R
, х є R
-
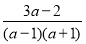 > 0
> 0
(a - 1) (a + 1)(a – ![]() ) > 0
) > 0
а є ( -1; ![]() )
) ![]() (1; + ∞)
(1; + ∞)
x ≥ ![]()
x є [![]() ; + ∞).
; + ∞).
-
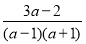 < 0
< 0
(a - 1) (a + 1)(a – ![]() ) < 0
) < 0
а є ( - ∞; - 1) ![]() (
(![]() ; 1)
; 1)
x ≤ ![]()
x є (- ∞ ; ![]() ].
].
Відповідь : якщо а є ( - ∞; - 1) ![]() (
(![]() ; 1), то x є (- ∞ ;
; 1), то x є (- ∞ ; ![]() ];
];
якщо а є ( -1; ![]() )
) ![]() (1; + ∞), то x є [
(1; + ∞), то x є [![]() ; + ∞);
; + ∞);
якщо а = + 1, то х є ![]() ;
;
якщо а = ![]() , то х є R;
, то х є R;
Приклад 8
При будь-якому значенні а розв’язати нерівність:
│ ![]() + x │< 3
+ x │< 3
Розв’язання :
│![]() + x │ < 3
+ x │ < 3
![]()
![]()
![]()
![]() + x > - 3, ax – 5 + 3x > - 9, (а + 3)х > - 4,
+ x > - 3, ax – 5 + 3x > - 9, (а + 3)х > - 4,
![]() + x < 3; ax – 5 + 3x < 9; (а + 3)х < 4;
+ x < 3; ax – 5 + 3x < 9; (а + 3)х < 4;
1) Якщо а = -3, то
![]()
0х > -4 х є R
0x < 14;
2) Якщо а < -3, то
![]()
x <-![]() ,
,
x >![]() ;
;
оскільки a + 3 < 0 при а є (- ∞; -3), то![]() <-
<-![]() , тому розв’язок системи : х є (
, тому розв’язок системи : х є (![]() ;-
;-![]() ).
).
3) Якщо а > -3, то
![]() х> -
х> -![]() ,
,
х< ![]() ;
;
Oскільки a + 3 > 0, то -![]() <
<![]() , тому розв’язок системи
, тому розв’язок системи
х є (-![]() ;
;![]() ).
).
Відповідь: Якщо а є (- ∞; -3), то х є (![]() ;-
;-![]() );
);
Якщо а є (-3; + ∞), то х є(-![]() ;
; ![]() );
);
Якщо а = -3, то х є R.
3)Квадратичними нерівностями з однією змінною називаються нерівності виду ax2 + bx + c >< 0, де a, b, c - дійсні числа і a ≠ 0
При розв’язуванні таких нерівностей з параметрами розглядаються випадки :
- Якщо a = 0, тоді нерівність лінійна
bx + c >< 0
- Якщо a ≠ 0, то нерівність другого степеня, розв’язувати її можна двома способами: графічно або методом інтервалів.
Графічний метод полягає в тому, що розглядається квадратична функція y = ax2 + bx + c, a ≠0 . Зображається схематично графік цієї функції з урахуванням напрямку віток ( a > 0 , вітки вгору; a < 0 , вітки вниз), та точок перетину графіка з осями координат ( D > 0), однією точкою на осі 0x ( D = 0 ), та жодних точок ( D < 0 ). Потім записуються розв’язки нерівності в залежності від її знака.
Метод інтервалів полягає в тому, що ліву частину нерівності розкладаємо на множини за формулою ax2 + bx + c = a(x-x1)(x-x2)
Нерівність приймає вигляд a(x-x1)(x-x2) >< 0 (1)
Методом інтервалів розв’язуються нерівності, подані у вигляді
(x - x1)(x - x2) … (x - xn) >< 0, де x1, x2, . . . xn – різні числа, що наносяться на числову вісь, розбиваючи її на проміжки. В крайньому правому проміжку ставимо знак „+”, решта знаків чергуються. Розставивши знаки, можна записати розв’язки даної нерівності.
Тому подальше розв’язання нерівності (1) залежатиме від знаку числа а, якщо a > 0, то нерівність прийме вигляд (x - x1)(x-x2) >< , а якщо a < 0 , то нерівність прийме вигляд (x - x1)(x - x2) >< 0.
Приклад 1
При будь-якому значенні а розв’язати нерівність
ax2 – 2(a -1)x + a +2<0
Розв’язання
ax2 – 2(a -1)x + a +2<0 (2)
1) a = 0; 2x + 2 < 0, x < - 1, x є (- ∞; - 1).
2) a > 0 , D1 = (a - 1)2 - a (a + 2) = a2 - 2a + 1 - a2 - 2a = -4a + 1.
A) D1 < 0,
- 4a + 1 < 0 ,
a >![]() , тобто а є (
, тобто а є (![]() ; + ∞)
; + ∞)
Схематичний графік функції у = ax2 – 2(a -1)x + a +2 в такому випадку має вигляд
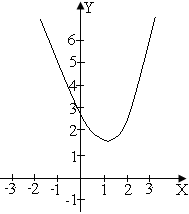
Тому розв’язок нерівності : х є ![]() .
.
Б) D1 > 0,
- 4a + 1 > 0
a <![]() , тобто а є (0;
, тобто а є (0; ![]() )
)
х1,2= ![]() - корені відповідного квадратного рівняння.
- корені відповідного квадратного рівняння.
Нерівність (2) в такому випадку прийме вигляд:
а (х -![]() ) (х -
) (х -![]() ) < 0;
) < 0;
(х -![]() ) (х -
) (х -![]() ) < 0.
) < 0.
Оскільки при а > 0 ![]() <
<![]() , тому
, тому
х є (![]() ;
;![]() ).
).
В) D1 = 0;
-4a + 1 = 0
a = ![]() .
.
![]() x2 – 2(-
x2 – 2(-![]() )x +
)x + ![]() +2 < 0
+2 < 0
![]() x2 +
x2 + ![]() x +
x + ![]() < 0
< 0
x2 + 6x + 9 < 0
(x + 3)2 < 0
x є ![]() .
.
3) а < 0
D1 > 0
a <![]() , тобто а є (- ∞ ; 0).
, тобто а є (- ∞ ; 0).
Нерівність (2) в такому разі прийме вигляд:
(х -![]() ) (х -
) (х -![]() ) < 0
) < 0
Оскільки а < 0, то , тому ![]() >
>![]() ,
,
х є (- ∞ ; ![]() )
)![]() (
( ![]() ; + ∞).
; + ∞).
Відповідь: якщо а = 0, то х є (- ∞; - 1);
якщо а є (0; ![]() ), то х є (
), то х є (![]() ;
;![]() );
);
якщо а є [![]() ; + ∞), то х є
; + ∞), то х є![]() ;
;
якщо а є (- ∞ ; 0), то х є(- ∞ ; ![]()
![]()
![]() )
)![]() (
( ![]() ; + ∞).
; + ∞).
Приклад 2
При будь-якому значенні а розв’язати нерівність
(2,5a + 1)x2 + (a + 2)x + a ≤ 0 (3).
Розв’язання
- 2,5а + 1 = 0
а =-![]() , 0х2 + (-
, 0х2 + (-![]() + 2)х –
+ 2)х –![]() ≤ 0
≤ 0
![]() x ≤
x ≤![]()
x ≤![]() , тобто х є (- ∞;
, тобто х є (- ∞;![]() ].
].
- 2,5а + 1 > 0
а > -![]() .
.
D = (a + 2)2 – 4 (2,5a + 1)a = a2 + 4a + 4 - 10a2 - 4a = - 9a2 + 4.
A) D > 0
- 9a2 + 4 > 0,
(a – ![]() )(a +
)(a + ![]() ) < 0,
) < 0,
a є (-![]() ;
;![]() ), тобто a є (-
), тобто a є (-![]() ;
;![]() ).
).
Корені квадратного тричлена х1,2=![]() .
.
![]()
![]()
![]() Нерівність (3) приймає вигляд
Нерівність (3) приймає вигляд
(2,5а + 1)(х-![]() )(х-
)(х-![]() ) ≤ 0,
) ≤ 0,
![]() тобто (х-
тобто (х-![]() )(х-
)(х-![]() ) ≤ 0.
) ≤ 0.
Оскільки 5а + 2 > 0 , то![]() <
<![]() , тому розв’язок нерівності (3) має вигляд:
, тому розв’язок нерівності (3) має вигляд:
х є [![]() ;
;![]() ].
].
Б) D < 0.
- 9a2 + 4 < 0,
(a –![]() )(a +
)(a +![]() ) > 0,
) > 0,
a є ( - ∞;-![]() )
) ![]() (
(![]() ; + ∞), тобто a є (
; + ∞), тобто a є (![]() ; + ∞).
; + ∞).
Схематичний графік квадратичної функції у =(2,5a + 1)x2 + (a + 2)x + a в такому випадку має вигляд:

Тому розв’язок нерівності (3) в такому випадку: х є![]() .
.
В) D = 0.
- 9a2 + 4 = 0,
a = +![]()
Проміжку а є (-![]() ; + ∞) належить тільки значення а =
; + ∞) належить тільки значення а = ![]() .
.
а =![]() , нерівність (3) при такому значенні а має вигляд :
, нерівність (3) при такому значенні а має вигляд :
![]() х2 +
х2 + ![]() х +
х +![]() ≤ 0,
≤ 0,
4x2 + 4x + 1 ≤ 0,
(2x + 1)2 ≤ 0 ,
x = - ![]() .
.
- 2,5а + 1 < 0,
а < - ![]() .
.
A) D > 0; а є (-![]() ;
;![]() ), тобто а є (-
), тобто а є (-![]() ; -
; -![]() ).
).
Нерівність (3) при таких значеннях параметра а приймає вигляд: (х-![]() )(х-
)(х-![]() ) ≥0.
) ≥0.
При ає(-![]() ; -
; -![]() )
) ![]() >
>![]() , тому розв’язок нерівності (3) в такому випадку має вигляд:
, тому розв’язок нерівності (3) в такому випадку має вигляд:
хє(-∞;![]() ]
]![]() [
[![]() ;+∞).
;+∞).
Б) D < 0 .
a є (- ∞ ; -![]() )
)![]() (
(![]() ; + ∞), тобто а є (- ∞ ; -
; + ∞), тобто а є (- ∞ ; - ![]() ).
).
Графік квадратичної функції у = (2,5a + 1)x2 + (a + 2)x + а при таких значеннях а має вигляд :
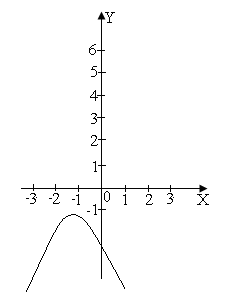
Тому розв’язок нерівності (3) при а є (- ∞ ; - ![]() ) х є R.
) х є R.
В) D = 0, а = - ![]() .
.
При такому значенні а нерівність (3) приймає вигляд :
-![]() х2 +
х2 + ![]() х –
х –![]() ≤ 0,
≤ 0,
х2 - 2х + 1 ≥ 0 ,
(x - 1)2 ≥ 0, x є R.
Відповідь :
якщо а є (- ∞ ; - ![]() ], то х є R;
], то х є R;
якщо а є (-![]() ; -
; - ![]() ), то х є (-∞;
), то х є (-∞;![]() ]
]![]() [
[![]() ;+∞) ;
;+∞) ;
якщо а = -![]() , то х є (- ∞;
, то х є (- ∞; ![]() ];
];
якщо a є (-![]() ;
; ![]() ), то х є [
), то х є [![]() ;
;![]() ];
];
якщо а =![]() , то x = -
, то x = - ![]() ;
;
якщо a є (![]() ; + ∞), то х є
; + ∞), то х є![]() .
.
Приклад 3
При яких значеннях k нерівність x2 - (k - 3)x – k + 6 > 0 справедлива при будь-якому х є R
Розв’язання
Оскільки графіком квадратичної функції у = x2 - (k - 3)x – k + 6 є парабола, вітки якої напрямлені вгору, то умова задачі виконується при
D < 0.
D = (k - 3)2- 4 . 1. (-k + 6) = k2 – 6k + 9 + 4k – 24 = k2 – 2k – 15;
k2 – 2k – 15 < 0;
(k - 5) (k + 3) < 0, k є (-3; 5).
Відповідь : k є (-3; 5).
Приклад 4
При яких значеннях а нерівність ax2 + 2ax + 0,5 > 0 виконується на всій числовій осі.
Розв’язання.
- a = 0,
0 . x2 + 2 . 0 . x + 0,5 > 0,
0x > - 0,5 , x є R.
![]()
2) a > 0,
D1 < 0;
D1 = а2 – 0,5а.
![]()
![]()
![]() a > 0, a > 0, а є (0 ; + ∞),
a > 0, a > 0, а є (0 ; + ∞),
а2 – 0,5а < 0; а (а – 0,5) < 0; а є (0; 0,5);
а є (0; 0,5).
Відповідь : а є [0; 0,5).
Приклад 5
Знайти всі значення а, для яких нерівність (a + 4)x2 – 2ax + 2a - 6 < 0 виконується для всіх х є R.
Розв’язання.
- а + 4 = 0, а = -4
8х – 14 < 0, х <![]() – умова задачі не задовольняється.
– умова задачі не задовольняється.
-
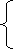 a + 4 < 0,
a + 4 < 0,
D1 < 0;
D1 = а2 – (a + 4)(2a - 6) = а2 - 2а2 + 6a – 8a + 24 = - а2 - 2a +24
![]()
![]()
![]() a + 4 < 0 a < -4, a < -4,
a + 4 < 0 a < -4, a < -4,
- а2 - 2a +24 < 0; а2 + 2a -24 > 0; (a + 6)(a - 4) > 0;
![]() a є (- ∞ ; -4),
a є (- ∞ ; -4),
a є (- ∞ ; -6) ![]() (4; + ∞); a є (- ∞ ; -6).
(4; + ∞); a є (- ∞ ; -6).
Відповідь : a є (- ∞ ; -6).
Приклад 6.
Знайти всі значення параметра а, при яких нерівність(а – 1)х2 + 2ах + 3а – - 2 > 0 (4) правильна на всій множині ( - 1; + ∞).
Розв’язання
Для того, щоб встановити всі значення параметра, які задовольнятимуть умову задачі, потрібно розглянути поступово всі види можливих розв’язків такої нерівності.
- а – 1 = 0, тобто а = 1.
0х2 + 2х + 3 – 2 > 0;
2x > - 1;
x > - ![]() .
.
Отже, розв’язки даної нерівності при значенні параметра а = 1 не задовольняють умову задачі.
- а – 1 > 0, a > 1.
- D < 0, при такій умові графік квадратичної функції y = (a – 2)x2 +
+ 2ax + 3a – 2 (5) – парабола, вітки якої напрямлені вгору, перетинає вісь абсцис у двох точках х1 і х2 (х1 < х2 ). При цьому розв’язок нерівності матиме вигляд : х є ( - ∞; х1) ![]() (х2 ; + ∞).Для того, щоб ці розв’язки були правильні на множині (- 1 ; + ∞) необхідно і достатньо, щоб x 1≤ x 2 ≤ - 1.
(х2 ; + ∞).Для того, щоб ці розв’язки були правильні на множині (- 1 ; + ∞) необхідно і достатньо, щоб x 1≤ x 2 ≤ - 1.
![]() Користуємося вказаним вище алгоритмом, щоб скласти умови, при яких це виконається.
Користуємося вказаним вище алгоритмом, щоб скласти умови, при яких це виконається.
а – 1 > 0,
D1 ≥ 0, (6)
- ![]() ≤ - 1;
≤ - 1;
(а – 1)f (- 1) ≥ 0
Знайдемо окремо D1, f (- 1), - ![]() .
.
D1 = а2 – (а – 1)(3а – 2) = а2 – 3а2 + 2а + 3а – 2 = - 2а2 + 5а – 2;
f (- 1) = (a – 1)(- 1)2 + 2a . (- 1) + 3a – 2 = a – 1 – 2a + 3a – 2 = 2a – 3;
- ![]() =
= ![]()
Отже, система (6) має вигляд: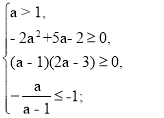
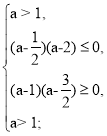
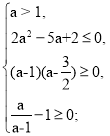
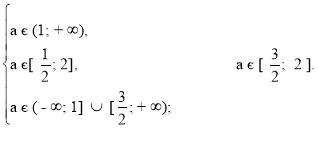
Б) D1 < 0, при такій умові графік квадратичної функції (5) – це парабола, вітки якої напрямлені вгору, що не перетинає вісь абсцис.
Розв’язок нерівності (4) в такому разі х є R, що задовольняє умову задачі.
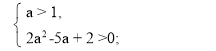
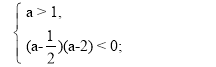
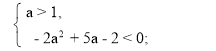
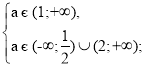
![]()
3) Випадок, коли а – 1 < 0, тобто а < 1 не задовольняє умову задачі, бо в разі, коли D1 > 0 розв’язком нерівності є проміжок (х1 ; х2), де х1 ; х2 – корені тричлена (х1 < х2), коли D1 ≤ 0, то нерівність (4) взагалі не має розв’язків.
Отже, об’єднавши отримані значення параметра а отримуємо відповідь.
Відповідь: а є [![]() ; + ∞).
; + ∞).
Приклад 5
Знайти а, при яких всі розв’язки першої нерівності будуть розв’язками другої ![]() ; x2 – 2ax + 4a + 4 > 0.
; x2 – 2ax + 4a + 4 > 0.
Розв’язання
Розв’яжемо першу дробово-раціональну нерівність:
![]() ,
,
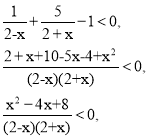 ,
,
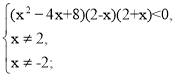
(х – 2)(х + 2) > 0,
х є ( - ∞; - 2) ![]() (2; + ∞).
(2; + ∞).
Розглянемо другу нерівність
x2 – 2ax + 4a + 4 > 0 (7)
Оскільки коефіцієнт при x2 дорівнює 1 > 0, то це звужує коло досліджень. Умова задачі буде задовольнятися лише в разі, коли корені х1 та х2 тричлена x2 – 2ax + 4a + 4 задовольняють умову – 2 ≤ х1 ≤ х2 ≤ 2 або коли D1 < 0.
D1 = a2 – 4a – 4;
f (- 2) = (- 2)2 – 2a(- 2) + 4a + 4 = 4 + 4a + 4a + 4 = 8a + 8;
f (2) = 22 – 2a.2 + 4a + 4 = 4 – 4a + 4a + 4 = 8;
- ![]() =
= ![]() = a.
= a.
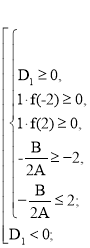

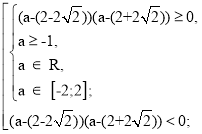
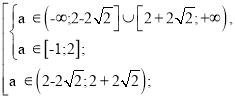
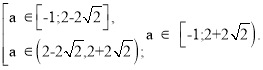
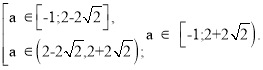
Відповідь :![]()
Приклад 6
Знайти всі значення а, при яких задана нерівність справджується на заданій множині.
ах2 – 2(а - 3)х + а + 3 > 0 (8), [- 2; 2]
Розв’язання
1) а = 0;
6х + 3 > 0, x > -![]() .Отже, при а = 0 розв’язок нерівності (8) не задовольняє умову задачі.
.Отже, при а = 0 розв’язок нерівності (8) не задовольняє умову задачі.
2) а > 0,
A) D1 < 0,
при такій умові графіком квадратичної функції у = ах2 –2(а -3)х + а + 3 є парабола, вітки якої напрямлені вгору, що не перетинає вісь абсцис. В такому випадку розв’язок нерівності (8) – х є R, що задовольняє умову задачі.
D1 = (а – 3)2 – а(а + 3) = 9 – 9а.
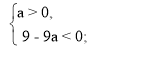
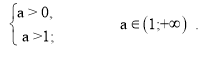
Б) D1 ≥ 0. При такій умові розв’язок нерівності (8) має вигляд
х є ( - ∞ ; х1 ) ![]() (x2 ; + ∞), де х1, x2 – корені тричлена.Для того, щоб при цьому задовольнялася умова задачі, потрібно, щоб х1≤ x2 < - 2 або
(x2 ; + ∞), де х1, x2 – корені тричлена.Для того, щоб при цьому задовольнялася умова задачі, потрібно, щоб х1≤ x2 < - 2 або
2 < х1 ≤ x2 . Знайдемо значення а , при яких виконаються ці умови.
f (- 2) = а(- 2)2 – 2(а – 3)(- 2) + а + 3 = 4а + 4а – 12 + а + 3 = 9а – 9;
f (2) = а(2)2 – 4(а – 3) + а + 3 = 4а - 4а + 12 + а + 3 = а + 15;
- ![]()
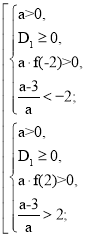
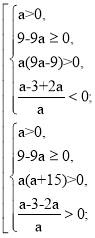
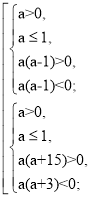
![]()
3) a < 0.
При умові, що вітки графіка функції у = ах2 – 2(а - 3)х + а + 3 напрямлені вниз, умова задачі задовольнятиметься лише тоді, коли числа – 2 і 2 знаходяться між коренями тричлена.
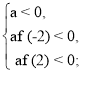
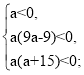
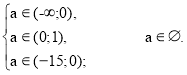
Отже, умова задачі задовольняється лише при а є ( 1; + ∞).
Відповідь: а є ( 1; + ∞).
Приклад 7
Знайти всі значення параметра а , при яких задана нерівність справджується на заданій множині.
(а2 – 4а + 3)х2 – (а – 1)х – 1 > 0; 0 < x < 1.
Розв’язання
- а2 – 4а + 3 = 0
а1 = 1, а2 = 3
а = 1, 0х2 – 0х – 1 > 0, 0x > 1, x є![]() .
.
а = 3 , 0х2 – 2х – 1 > 0, 2х > - 1, х є (- ∞; -![]() ).
).
Отже, при вказаних значеннях параметра а (1 та 3) розв’язки нерівності не задовольняють умову задачі.
2) а2 – 4а + 3 > 0, (а – 1)(а – 3) > 0, а є ( - ∞; 1) ![]() ( 3; + ∞).
( 3; + ∞).
А) Якщо D < 0, то х є R.
D = (a – 1)2 – 4(а2 – 4а + 3)(- 1) = a2 – 2a + 1 + 4a2 – 16a + 12 =
= 5a2 – 18a + 13.
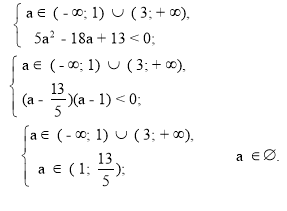
Б) Якщо D ≥ 0, то корені х1 та х2 квадратного тричлена (а2 – 4а + 3)х2 –
- (а – 1)х – 1 мають задовольняти умови:
х1 ≤ х2 ≤ 0 або 1 ≤ х1 ≤ х2.
Зробимо додаткові розрахунки :
f (0) = - 1,
f (1) = а2 – 4а + 3 – a + 1 – 1 = а2 – 5а + 3,
- ![]()
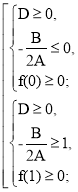
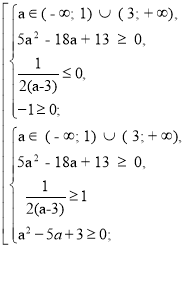

![]()
3) а2 – 4а + 3 < 0, (а – 1)(а – 3) > 0, а є (1; 3)
Якщо D ≤ 0, то розв’язок даної нерівності х є ![]() .
.
Якщо D > 0, то щоб виконувалася умова задачі, потрібно щоб числа 0 і 1 знаходилися між коренями тричлена (а2 – 4а + 3)х2 – (а – 1)х – 1 .
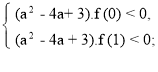
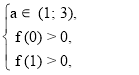
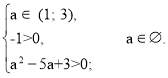
Отже, не існує значень параметра а, при яких виконується умова задачі.
Відповідь: ![]()
Приклад 8
Знайти всі значення параметра а, при кожному з яких множина розв’язків нерівності х2 – (а + 1)ах + а3 ≤ 0 містить не менше п’яти цілих значень х.
Розв’язання
Оскільки у лівій частині нерівності знаходиться квадратний тричлен, у якого коефіцієнт при х2 дорівнює числу 1> 0, то для того, щоб дана нерівність мала розв’язки необхідно, щоб D > 0.
Знайдемо D:
D = ( (а + 1)а)2 – 4а3 = (а2 + а)2 – 4а3 = а4 + 2а3 + а2 – 4а3 = а4 - 2а3 + а2 =
= а2 (а2 - 2а + 1) = (а(а – 1) )2.
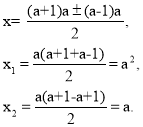
Якщо а < 0, то розв’язок нерівності : х є [a; a2]
Якщо – 1 < а ≤ 0, то розв’язок нерівності не містить п’яти цілих
чисел.
Якщо – 2 < а ≤ - 1, то найменший цілий розв’язок х = - 1 за умовою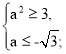
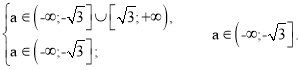
2) Нехай а ≥ 0.
Якщо 0 ≤ а ≤ 1, то немає п’яти цілих значень х, при яких а2 ≤ х ≤ а.
Якщо а > 1, то розв’язок нерівності а ≤ х ≤ а2 .
Якщо 1 < а ≤ 2, то для того, щоб виконалася умова задачі, потрібно щоб а2 ≥ 6. Ці умови несумісні.
Якщо 2 < а ≤ 3, то а2 ≥ 7, отже а ≥ ![]() .
.
Всі значення а, при яких а > 3 умову задачі задовольняють, бо якщо
3 ≤ n ≤ a < n + 1, то a2 ≥ n2 і нерівність задовольняють всі цілі від
n + 1 до n2 . Їх кількість не менше п’яти.
Відповідь: а ≤ -![]() або а ≥
або а ≥ ![]() .
.
Розв’яжемо дробово-раціональні нерівності з параметрами, застосовуючи при цьому метод інтервалів. Оскільки знак дробу такий самий, як і знак відповідного добутку, при умові, що знаменник не дорівнює нулю, то розв’язання дробово-раціональних нерівностей будемо здійснювати за наступним алгоритмом:
- Всі вирази з правої частини нерівності переносимо вліво, змінюючи знаки на протилежні.
- Зводимо дроби в лівій частині нерівності до спільного знаменника.
- Замінюємо частку на добуток, при умові , що знаменник не дорівнює нулю.
- Готуємо нерівність до методу інтервалів і застосовуємо цей метод до розв’язання даної нерівності.
Приклад 1
При будь-якому значенні параметра b розв’язати нерівність
![]()
Розв’язання
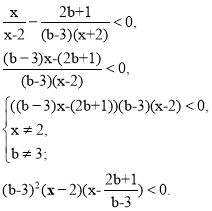
Якщо b ≠ 3, то (x - 2)(x – ![]() ) < 0.
) < 0.
Встановимо взаємне розташування чисел 2 і![]() при різних значеннях b .
при різних значеннях b .
Знайдемо ті значення b, при яких 2 > ![]() .
.
2 -![]() > 0,
> 0,
![]() -7 (b - 3) > 0,
-7 (b - 3) > 0,
b – 3 < 0,
b < 3.
Отже, при b < 3, 2 >![]() , а при b > 3, 2 <
, а при b > 3, 2 < ![]() .
.
- Якщо b < 3, то
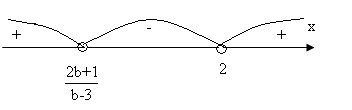 х є (
х є (![]() ; 2 ).
; 2 ).
2) Якщо b > 3, то
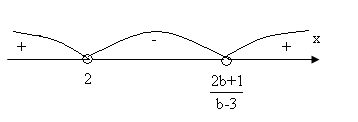
х є ( 2 ; ![]() ).
).
Відповідь : якщо b є ( - ∞ ; 3) , то х є (![]() ; 2 );
; 2 );
якщо b = 3, то х є ![]() ;
;
якщо b є ( 3; + ∞), то х є ( 2 ; ![]() ).
).
Приклад 2
При будь-якому значенні параметра а розв’язати нерівність
![]() .
.
Розв’язання
![]() ,
,
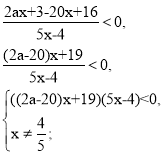
1) 2a – 20 = 0 , a = 10.
19(5x – 4) < 0; x < ![]() .
.
2) 2a – 20 > 0, a > 10.
(x +![]() ) (x –
) (x –![]() ) < 0.
) < 0.
Встановимо взаємне розташування чисел -![]() та
та![]() в залежності від параметра а.
в залежності від параметра а.
-![]() >
>![]() ,
,
-![]() -
- ![]() >0,
>0,
![]() +
+ ![]() <0,
<0,
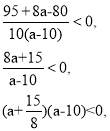
a є (-![]() ; 10).
; 10).
Очевидно, що-![]() <
<![]() при а є ( - ∞;-
при а є ( - ∞;-![]() )
)![]() (10 ; + ∞).
(10 ; + ∞).
Оскільки ми розглядаємо випадок a > 10, то
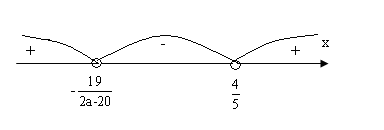
Отже , х є (-![]() ;
;![]() ).
).
- a < 10, нерівність приймає вигляд :
(x +![]() ) (x –
) (x –![]() ) > 0.
) > 0.
3a) а є ( - ∞;- ![]() ).
).

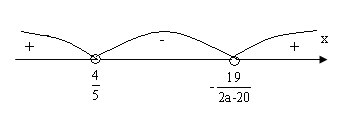
хє(- ∞ ; -![]() )
)![]() (
(![]() ;+∞).
;+∞).
3б) а = -![]() .
.
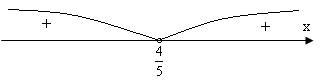
а є ( - ∞;![]() )
)![]() (
(![]() ; + ∞).
; + ∞).
Випадок а = -![]() можна включити в попередній.
можна включити в попередній.
3в) а є ( -![]() ; 10).
; 10).

х є (- ∞;![]() )
)![]() ( -
( -![]() ; + ∞ ).
; + ∞ ).
Відповідь : якщо а є ( - ∞ ; -![]() ], то х є хє(- ∞ ; -
], то х є хє(- ∞ ; -![]() )
)![]() (
(![]() ;+∞);
;+∞);
якщо а є (-![]() ; 10), то х є (- ∞;
; 10), то х є (- ∞;![]() )
)![]() ( -
( -![]() ; + ∞ ); якщо а = 10, то х є ( - ∞ ;
; + ∞ ); якщо а = 10, то х є ( - ∞ ; ![]() );
);
якщо а є (10; + ∞), то х є (-![]() ;
;![]() ).
).
Приклад 3.
При будь-якому значенні параметра а розв’язати нерівність
![]()
Розв’язання
![]()
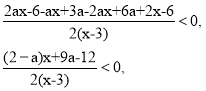
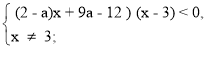
1) a = 2.
6(x – 3) < 0,
x < 3,
х є (- ∞ ; 3).
2) 2 – а > 0, a < 2.
( 2 – a) ( x +![]() ) (x – 3) < 0,
) (x – 3) < 0,
( x +![]() ) (x – 3) < 0.
) (x – 3) < 0.
Встановимо взаємне розташування чисел - ![]() і 3 в залежності від параметра а.
і 3 в залежності від параметра а.
Знайдемо значення параметра а, при яких - ![]() < 3.
< 3.
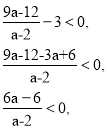
( a – 1) (a – 2) < 0,
a є (1 ; 2).
Знайдемо значення параметра а , при яких- ![]() > 3.
> 3.
( a – 1) (a – 2) > 0,
а є ( - ∞; 1)![]() ( 2 ; + ∞).
( 2 ; + ∞).
Враховуючи, що випадок, який ми розглядаємо a < 2 , то- ![]() > 3
> 3
при а є ( - ∞ ; 1).
Якщо а = 1, то- ![]() = 3.
= 3.
Отже, розглянемо випадки:
2а) а є (- ∞ ; 1).
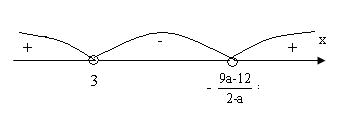
х є (3 ; ![]() ).
).
2б) а = 1.
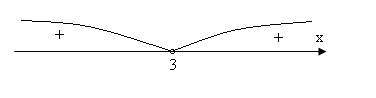
х є![]() .
.
2в) а є ( 1 ; 2).
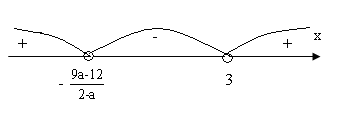
х є (![]() ; 3).
; 3).
3) 2 – а < 0,
a > 2,
(2 – a) ( x-![]() ) (x – 3) < 0,
) (x – 3) < 0,
( x -![]() ) (x – 3) > 0,
) (x – 3) > 0,

х є х є (![]() ; 3) ( - ∞ ; 3)
; 3) ( - ∞ ; 3) ![]() (
(![]() ; + ∞ ).
; + ∞ ).
Відповідь : якщо а є (- ∞ ; 1), то х є х є (3 ; ![]() );
);
якщо а = 1, то х є![]() ;
;
якщо а є ( 1 ; 2) , то х є (![]() ; 3);
; 3);
якщо а = 2, то х є (- ∞ ; 3);
якщо а є ( 2 ; + ∞) , то х є х є (![]() ; 3).
; 3).
Приклад 4
При будь-якому значенні параметра а розв’язати нерівність.
![]() .
.
Розв’язання
![]() , a
, a![]() 1.
1.
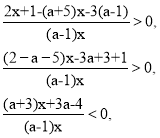
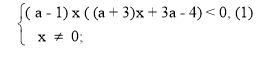
I) a – 1 > 0, a > 1 , a є ( 1 ; + ∞ ).
х ( ( а + 3)х + 3а – 4) < 0.
При a > 1, а + 3 > 0, тому нерівність (1) приймає вигляд:
х ( х +![]() ) < 0 (2).
) < 0 (2).
Встановимо взаємне розташування чисел 0 і -![]() .
.
Знайдемо, при яких значеннях параметра а- ![]() < 0.
< 0.
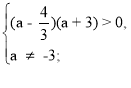
а є (- ∞ ; - 3) ![]() (
(![]() ; + ∞ ).
; + ∞ ).
Очевидно , якщо а є ( - 3; ![]() ), то -
), то -![]() > 0.
> 0.
Якщо а =![]() , то-
, то-![]() = 0.
= 0.
Маємо випадки :
І а) Нехай а є ( 1; ![]() ). Розв’яжемо нерівність (2) методом інтервалів.
). Розв’яжемо нерівність (2) методом інтервалів.
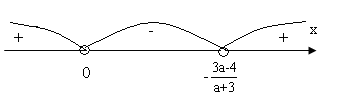
х є ( 0 ; -![]() ).
).
Iб) Нехай а =![]() , то нерівність (2) прийме вигляд х2 < 0.
, то нерівність (2) прийме вигляд х2 < 0.
Її розв’язок х є![]() .
.
Ів) Нехай а є (![]() ; + ∞ ).
; + ∞ ).
Розв’яжемо нерівність (2) методом інтервалів.
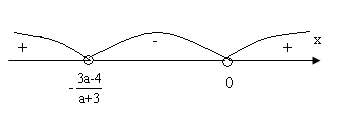
х є (-![]() ; 0).
; 0).
ІІ. а – 1 < 0 , a < 1, a є ( - ∞ ; 1).
При таких значеннях а нерівність (3) приймає вигляд :
x ((a + 3)x + 3a – 4 ) > 0. (3)
1) a + 3 < 0, a < - 3.
При таких значеннях а нерівність (3) приймає вигляд :
(а + 3)х (х +![]() ) > 0,
) > 0,
х (х +![]() ) < 0. (4)
) < 0. (4)
При a < - 3 число -![]() менше, ніж 0. Зображаємо їх на числовій осі та нерівність (4) розв’язуємо методом інтервалів.
менше, ніж 0. Зображаємо їх на числовій осі та нерівність (4) розв’язуємо методом інтервалів.

х є (-![]() ; 0).
; 0).
2) а + 3 = 0, а = -3.
х ∙(- 13) > 0;
x < 0, x є (- ∞ ; 0).
3) a + 3 > 0
a > - 3, a є (- 3; 1).
При таких значеннях а число -![]() більше, ніж 0, а нерівність(3) приймає вигляд х (х +
більше, ніж 0, а нерівність(3) приймає вигляд х (х + ![]() ) > 0.
) > 0.

х є (- ∞ ; 0) ![]() (-
(-![]() ; + ∞ ).
; + ∞ ).
Відповідь : якщо а є (- ∞ ; - 3) ![]() (
(![]() ; +∞ ), то х є (-
; +∞ ), то х є (-![]() ; 0);
; 0);
якщо a є (- 3; 1), то х є (- ∞ ; 0) ![]() (-
(-![]() ; + ∞ );
; + ∞ );
якщо а є ( 1; ![]() ), то х є ( 0 ; -
), то х є ( 0 ; -![]() );
);
якщо а = 1, а =![]() , то х є
, то х є ![]() ;
;
якщо а = - 3, то х є( - ∞ ; 0).
При розв’язуванні ірраціональних нерівностей з параметрами будемо користуватися наступним алгоритмом:
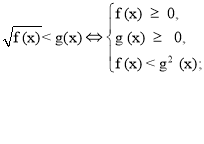
![]()
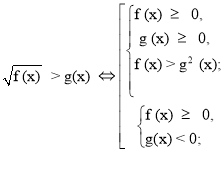
Приклад 1
При будь-якому значенні параметра а розв’язати нерівність ![]() .
.
Розв’язання
![]()
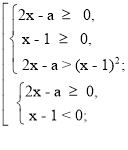
Розв’яжемо першу систему сукупності.
![]() x ≥
x ≥ ![]() ,
,
x ≥ 1, (1)
x2 – 4x + 1 + a < 0;
Розглянемо квадратну нерівність x2 – 4x + 1 + a < 0.
x2 – 4x + 1 + a = 0.
D1 = 4 – а – 1 = 3 – а.
Якщо D1 ≤ 0, тобто 3 – а ≤ 0, а ≥ 3, то нерівність x2 – 4x + 1 + a < 0 розв’язків не має, а отже і не має розв’язків система.
![]() Якщо D1 > 0, тобто 3 – а > 0, а < 3, то корені рівняння х = 2±
Якщо D1 > 0, тобто 3 – а > 0, а < 3, то корені рівняння х = 2±![]() , а нерівність приймає вигляд:
, а нерівність приймає вигляд:
(х – (2 +![]() ) ) (х – (2 -
) ) (х – (2 -![]() ) ) < 0,
) ) < 0,
х є (2 - ![]() ; 2 +
; 2 +![]() ).
).
Отже, система (1) приймає вигляд:
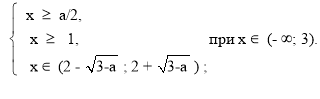
Щоб розв’язати цю систему, встановимо взаємне розташування чисел:
![]() ; 1 ; 2 -
; 1 ; 2 -![]() ; 2 +
; 2 + ![]() .
.
Порівняємо![]() і 1.
і 1.
1 >![]() —?
—?
a < 2.
Отже, при а є ( - ∞ ; 2), 1 > ![]() ; при а = 2, 1 =
; при а = 2, 1 =![]() ; при а є (2; 3), 1 <
; при а є (2; 3), 1 <![]() .
.
Порівняємо 2 - ![]() >
> ![]() .
.
2 - ![]() >
> ![]() ,
,
![]() < 2 -
< 2 - ![]() ,
,
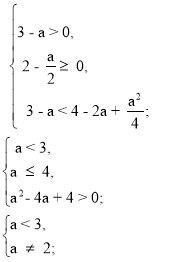
![]() Отже, при а є (- ∞ ; 2)
Отже, при а є (- ∞ ; 2) ![]() (2; 3), 2 -
(2; 3), 2 - ![]() >
>![]() ; при а = 2 , 2 -
; при а = 2 , 2 - ![]() =
=![]() .
.
Встановимо , як залежить розташування чисел 2 - ![]() і 1.
і 1.
2 - ![]() < 1—?
< 1—?
![]() > 1;
> 1;
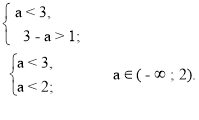
Отже при а є ( - ∞; 2), ![]() > 1.
> 1.
![]() < 1;
< 1;
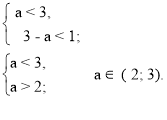
Отже, при а є (2; 3) ![]() < 1.
< 1.
При а = 2 ![]() = 1.
= 1.
Встановимо взаємне розташування чисел 2 + ![]() і 1 - ?
і 1 - ?
2 + ![]() > 1,
> 1,
![]() > - 1,
> - 1,
a < 3.
Отже при всіх а є (- ∞ ; 3) 2 + ![]() > 1.
> 1.
Таким чином можна розглядати наступні випадки для параметра а
Якщо а є ( - ∞; 2) , то числа на осі х розташовані наступним чином:
![]() < 2 -
< 2 - ![]() < 1 < 2 +
< 1 < 2 +![]() .
.
Розв’яжемо систему (1) в такому випадку :

х є [ 1 ; 2 +![]() ).
).
Якщо а = 2, то ![]() = 2 -
= 2 - ![]() = 1.
= 1.
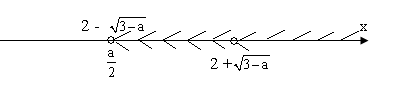
х є (1 ; 2 + ![]() ).
).
Якщо а є (2; 3), то числа на осі х розташовані наступним чином:
1 <![]() < 2 -
< 2 - ![]() < 2 +
< 2 + ![]() .
.
Розв’яжемо систему (1) в такому випадку:
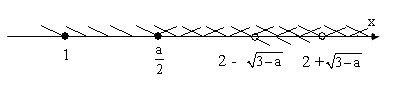
х є (2 - ![]() ; 2 +
; 2 + ![]() ).
).
Розв’яжемо другу систему сукупності:
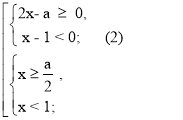
Якщо а є (- ∞; 2), то 1 >![]() ; якщо а = 2, то 1 =
; якщо а = 2, то 1 = ![]() ; якщо а є (2; + ∞), то
; якщо а є (2; + ∞), то
1 < ![]() .
.
При а є ( - ∞; 2)

х є [![]() ; 1).
; 1).
При а є [ 2 ; + ∞) х є ![]() .
.
Об’єнуємо отримані розв’язки систем.
Відповідь: якщо ( - ∞; 2), то х є [![]() ;2 +
;2 + ![]() );
);
якщо а є [ 2 ; 3) , то х є (2 - ![]() ; 2 +
; 2 + ![]() );
);
якщо а є [ 3; + ∞), то х є![]() .
.
Приклад 2
![]() При будь-якому значенні параметра а розв’язати нерівність
При будь-якому значенні параметра а розв’язати нерівність ![]() Розв’язання.
Розв’язання.
![]()
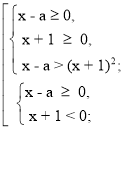
Розв’яжемо першу систему сукупності:
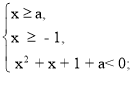
x2 + х + 1 + а < 0;
x2 + х + 1 + а = 0;
D = 1 – 4(1 + a) = 1 – 4 - 4a = - 4a – 3.
При D ≤ 0 многочлен x2 + х + 1 + а набуває додатних значень, тому при
- 4a – 3 ≤ 0, a ≥ - ![]() нерівність не має розв’язків і не має розв’язків система .
нерівність не має розв’язків і не має розв’язків система .
Якщо D > 0, - 4а – 3 > 0, а < - ![]() .
.
Корені тричлена x2 + х + 1 + а:
х1 = 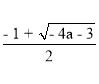 ; х 2 =
; х 2 =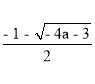 .
.
Отже нерівність приймає вигляд :
( х - 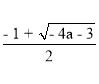 ) (х-
) (х- 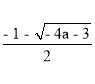 ) < 0,
) < 0,
х є (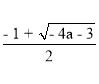 ;
;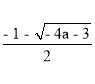 ).
).
Для розв’язання системи потрібно встановити взаємне розташування чисел а ; - 1; 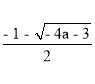 ;
; 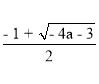 .
.
При а < - 1, а < 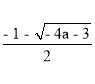 < - 1 <
< - 1 <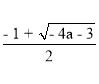 .
.
Розв’язуємо систему:
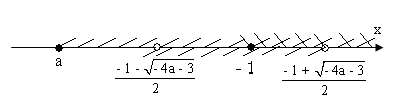
х є [- 1; 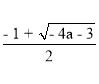 ).
).
Якщо а = - 1, то 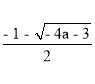 = - 1.
= - 1.
х є (- 1; 0).
Якщо а є (- 1; -![]() ) , то - 1 < а <
) , то - 1 < а < 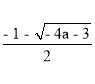 <
<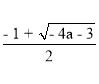 .
.
Розв’язуємо систему:
х є (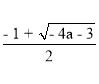 ; (
; (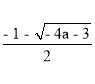 ).
).
Розвяжемо другу систему сукупності:
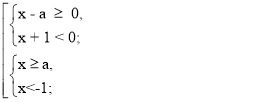
Якщо a < - 1, то
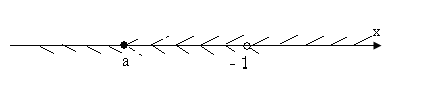
х є [ а; - 1).
Якщо а ≥ - 1, то х є ![]() .
.
Об’єднаємо отримані розв’язки.
Відповідь : якщо а є (- ∞; - 1) , то х є [ а; 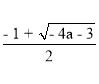 );
);
якщо а є [- 1; - ![]() ), то х є (
), то х є ( 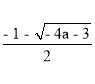 ;
; 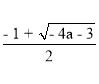 );
);
якщо а є [-![]() ; + ∞), то х є
; + ∞), то х є ![]() .
.
Приклад 3
При будь-якому значенні параметра а розв’язати нерівність
![]() .
.
Розв’язання
![]() ,
, 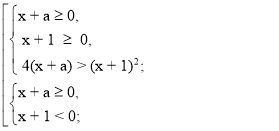
Розвяжемо першу систему сукупності:
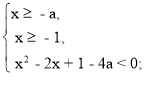
x2 – 2х + 1 – 4а = 0,
D1 = 1 – 1 + 4a = 4a.
Якщо D1 ≤ 0, тобто а ≤ 0, то квадратна нерівність системи не має розв’язків, а отже не має розв’язків і система.
Якщо а > 0, то нерівність приймає вигляд:
(х – (1 + 2![]() ) ) (х – (1 - 2
) ) (х – (1 - 2![]() ) ) < 0,
) ) < 0,
х є (1 - 2![]() ; 1 + 2
; 1 + 2![]() ).
).
Встановимо взаємне розташування чисел: - а, - 1, 1 - 2![]() , 1 + 2
, 1 + 2![]() при
при
а > 0.
- – a < - 1, тобто a > 1;
1 - 2![]() > - 1, при 0< a < 1;
> - 1, при 0< a < 1;
1 - 2![]() < - 1, при a > 1;
< - 1, при a > 1;
1 - 2![]() > - a, при a є (0; 1)
> - a, при a є (0; 1) ![]() (1; + ∞);
(1; + ∞);
1 + 2![]() > - 1, при a > 0.
> - 1, при a > 0.
Тому, при a > 1
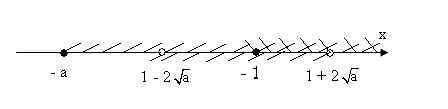
х є [ - 1; 1 + 2![]() ).
).
2) – a = - 1, тобто а = 1.
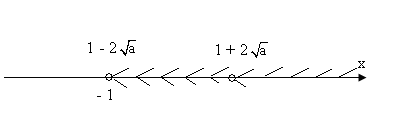
х є ( - 1; 1 + 2![]() ).
).
3) – а > - 1, а є (0; 1).
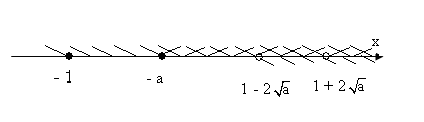
х є (1 - 2![]() ; 1 + 2
; 1 + 2![]() ).
).
Розвяжемо другу систему сукупності.
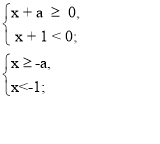
- – a < - 1 , a > 1.
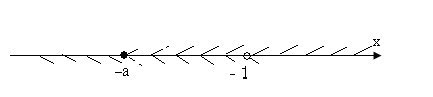
х є [ - a; 1) .
-
- а ≥ - 1, a ≤ 1,х
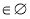 .
.
Об’єднуємо розв’язки систем.
Відповідь: якщо а є (- ∞ ; 0], то х ![]() ;
;
якщо а є (0; 1], то х є (1 - 2![]() ; 1 + 2
; 1 + 2![]() );
);
якщо а є ( 1 ;+ ∞), то х є [ - a ; 1 + 2![]() ).
).
Приклад 4.
При будь-якому значенні параметра а розв’язати нерівність:
![]() .
.
Розв’язання
![]()
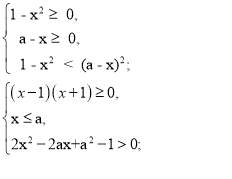
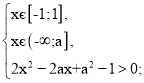
Розв’яжемо квадратну нерівність :
2x2 – 2ax + a2 – 1 > 0.
D1 = a2 – 2a2 +2 = 2 - a2,
Якщо D1 < 0, тобто 2 - a2 < 0, (а – ![]() )(а +
)(а + ![]() ) > 0,
) > 0,
а є ( - ∞; - ![]() )
) ![]() (
(![]() ; + ∞) ,то х є R.
; + ∞) ,то х є R.
Якщо D1 ≥ 0, тобто 2 - a2 ≥ 0, (а –![]() )(а +
)(а + ![]() ) ≤ 0,
) ≤ 0,
а є [-![]() ;
; ![]() ], то корені тричлена :
], то корені тричлена :
х1 = ![]() та х2 =
та х2 = ![]() , а розв’язки нерівності
, а розв’язки нерівності
х є (- ∞; ![]() )
) ![]() (
(![]() ; + ∞).
; + ∞).
Встановимо взаємне розташування чисел :
-1; 1; а; ![]() ;
; ![]() .
.
При а є [-![]() ; - 1) a < - 1 <
; - 1) a < - 1 <![]() <
< ![]() < 1.
< 1.
Розв’яжемо систему в такому випадку
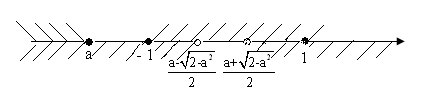
х є ![]() .
.
а = - 1.
х є ![]() .
.
Якщо а є ( - 1; 1), то – 1 <![]() < a <
< a <![]() < 1.
< 1.
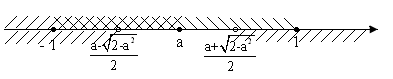
x є [ - 1; ![]() ).
).
Якщо а = 1

х є [ - 1; ![]() ).
).
Якщо а є (1; ![]() √2 ], то – 1 <
√2 ], то – 1 < ![]() (а – √2 – а2) / 2 <
(а – √2 – а2) / 2 < ![]() (а + √2 – а2) / 2 < 1 < a
(а + √2 – а2) / 2 < 1 < a
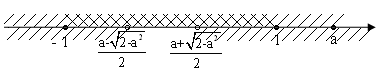
х є [ - 1; ![]() )
) ![]() (
(![]() ; 1].
; 1].
![]() Якщо а є ( - ∞; -
Якщо а є ( - ∞; - ![]() )
)![]() (
(![]() ; + ∞), то система приймає вигляд :
; + ∞), то система приймає вигляд :
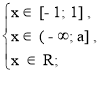
Якщо а < - ![]() , то х
, то х![]() .
.
Якщо а > ![]() , то х є [– 1; 1].
, то х є [– 1; 1].
Відповідь : якщо а є ( - ∞; - 1] , то х![]() ;
;
якщо а є (– 1; 1] , то х є [ - 1; ![]() );
);
якщо а є (1; ![]() ], то х є [ - 1;
], то х є [ - 1; ![]() )
) ![]() (
(![]() ; 1];
; 1];
якщо а є (![]() ; + ∞), то х є [– 1; 1].
; + ∞), то х є [– 1; 1].
Приклад 5
Для кожного значення параметра а розв’язати нерівність ![]() .
.
Розв’язання
![]()
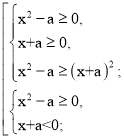
Нехай а > 0, тоді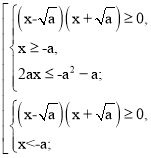

Встановимо взаємне розташування чисел :![]() ; -
; - ![]() ; - а; -
; - а; -![]() .
.
Якщо 0 < а < 1, то а < ![]() <
< ![]() , тобто –
, тобто – ![]() < –
< – ![]() < – а.
< – а.
Розв’яжемо кожну із систем сукупності

х![]() – розв’язок першої системи.
– розв’язок першої системи.
![]()
х є (- ∞; – ![]() ].
].
Отже, розв’язок сукупності при 0 < а < 1, х ![]() (- ∞; –
(- ∞; –![]() ].
].
а = 1
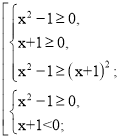
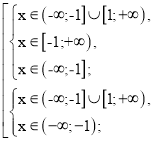
![]() ,
,
Об’єднуємо : х ![]() (- ∞; – 1 ].
(- ∞; – 1 ].
Якщо a > 1, то ![]() <
<![]() < a, тобто – a < -
< a, тобто – a < - ![]() < -
< -![]() .
.

х![]() [ - a ; -
[ - a ; -![]() ] - розв’язок першої системи сукупності.
] - розв’язок першої системи сукупності.
![]() .
.![]()
2) Нехай а = 0
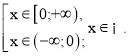
3) Нехай а < 0
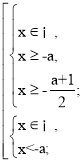
Порівняємо числа а і![]() .
.
а –![]() =
=![]() < 0, при a < 1.
< 0, при a < 1.
Отже a < ![]() , тому - a > -
, тому - a > -![]() .
.

х є [ - а; + ∞) – розв’язок першої системи,
х є ( - ∞; - а) – розв’язок другої системи.
Об’єднуємо отримані розв’язки : х є R.
Відповідь : якщо а є ( - ∞; 0], то х є R;
якщо а є (0; 1), то х є (- ∞; – ![]() ];
];
якщо а є [1; + ∞), то х є ( - ∞; - ![]() ].
].
Приклад 6
![]()
![]()
![]() Для всіх значень параметра а розв’язати нерівність
Для всіх значень параметра а розв’язати нерівність ![]() .
.
Розв’язання
![]()
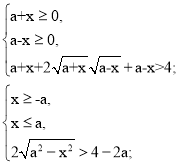
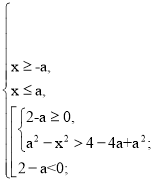
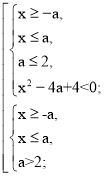
Розв’яжемо першу систему сукупності.
Перші дві нерівності системи дають розв’язок, якщо а ≥ 0. Якщо а < 0, то перша система розв’язків не має.
а) 0 ≤ а ≤ 1, то х2 < 4а – 4 не має розв’язків (4а – 4 ≤ 0, а ≤ 1), а отже не має розв’язків і система.
б) Нехай а є (1 ; 2).
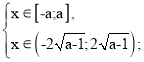
Встановимо взаємне розташування чисел а і![]() .
.
Якщо ![]() , то а >
, то а >![]() .
.

х є (-![]() ;
;![]() ).
).
в) а = 2
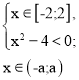
Розв’яжемо другу систему сукупності
![]() х
х ![]() [– а; а],
[– а; а],
а![]() (2; + ∞);
(2; + ∞);
Отже, при а![]() (2; + ∞) , х
(2; + ∞) , х ![]() [– а; а].
[– а; а].
Відповідь : якщо а ![]() ( - ∞; 1], то х
( - ∞; 1], то х ![]() ;
;
якщо а ![]() (1 ; 2], то х
(1 ; 2], то х![]() (-
(-![]() ;
; ![]() );
);
якщо а ![]() (2; + ∞) , то х
(2; + ∞) , то х ![]() [– а; а].
[– а; а].
Приклад 7
Для всіх значень параметра а розв’язати нерівність ![]() .
.
Розв’язання
![]()
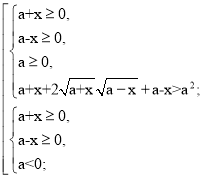
Розв’яжемо першу систему сукупності.
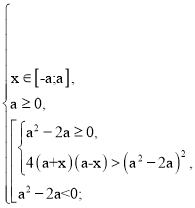
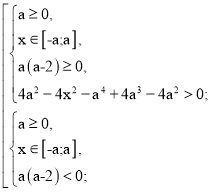
Розв’яжемо нерівність
4а2 – 4х2 – а4 + 4а3 – 4а2 > 0,
4х2 + а4 - 4а3 < 0,
х2 < а3 - ![]() .Якщо а3 -
.Якщо а3 -![]() < 0, то нерівність розв’язків не має.
< 0, то нерівність розв’язків не має.
Тобто а3(а – 4) ≥ 0,а є ( - ∞; 0] ![]() [4; + ∞), то х
[4; + ∞), то х![]() .
.
Якщо а3 -![]() ≥ 0; а4 – 4а3 ≤ 0,а
≥ 0; а4 – 4а3 ≤ 0,а ![]() (0; 4), то
(0; 4), то
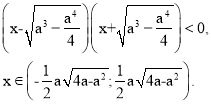
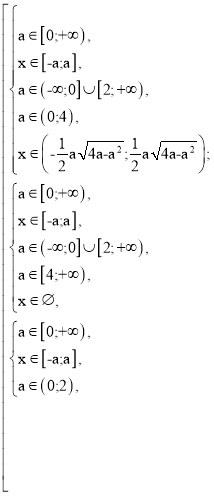
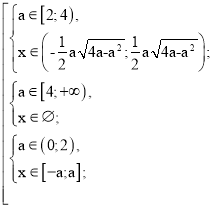
Розглянемо другу систему сукупності:
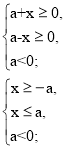 х
х ![]() .
.
Відповідь : якщо а ![]() ( - ∞; 0]
( - ∞; 0] ![]() [4; + ∞), то х
[4; + ∞), то х![]() ;
;
якщо а![]() (0; 2), то х
(0; 2), то х ![]() [– а; а];
[– а; а];
якщо а ![]() [2; 4), то
[2; 4), то ![]()
Література
- О.Г. Гайштут, Г. М. Литвиненко „Розв’язування алгебраїчних задач”, Київ „Радянська школа”, 1991.
- І.Ф. Шаригін „Факультативний курс з математики. Розв’язування задач 10”, Москва „Просвещение”, 1989
- В.Н. Литвиненко, А. Г. Мордкович „Практикум з елементарної математики”, Москва „Просвещение”, 1991.
- В.В. Ясінський „Математика. Методичний посібник для слухачів ІДП НТУУ „К П І ” ”, Київ, 2004.
-
-
ДЯКУЮ!


про публікацію авторської розробки
Додати розробку
