Збірка математичних диктантів для учнів 11 класу по розділу: “Многогранники”

Тема:Многогранники. Призма.

№

Зміст запитання

Відповідь

1.

Чи вірно,що площею поверхні многогранника вважають суму площ усіх бічних граней?

Невірно

2.

Як називають многокутники, котрі обмежують многогранник?

Грані

3.

Як називають відрізки, котрі сполучають вершини многогранника, які не належать одній грані?

Діагональ

4.

Скільки діагоналей має куб?

4

5.

Чи вірно, що кожен многогранник є призмою?

Невірно

6.

Як називають призму, основою якої є паралелограм?

Паралелепіпед

7.

Чи кожен куб є паралелепіпедом?

Так

8.

Як називають переріз призми площиною, яка проходить через бічне ребро і діагональ основи призми?

Діагональний переріз

9.

Як обчислити бічну поверхню призми?

S=ph

10.

Як називають призму, в якої бічні ребра не є перпендикулярними до площини основи призми?

Похилою призмою

11.

Чи може дана розгортка бути розгорткою куба?

Так

12.

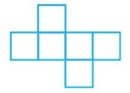
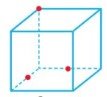
Який многокутник є перерізом, що проходить через вказані точки куба?

Трикутник

Тема: Піраміда

№

Зміст запитання

Відповідь

1.

Чи всі піраміди є тетраедрами?

Ні

2.

Як називають точку піраміди, яка є спільною точкою всіх бічних ребер?

Вершиною піраміди

3.

Чи всі грані піраміди є трикутниками?

Ні

4.

Як називають перпендикуляр, опущений з вершини піраміди до площини основи?

Висотою піраміди

5.

Як називають перпендикуляр, опущений з вершини правильної піраміди до сторони її основи?

Апофема

6.

Як обчислити площу бічної поверхні правильної піраміди?

Добуток півпериметра основи на апофему

7.

Як називається многогранник, зображений на малюнку та Н1Н

відрізок

Зрізана піраміда, висота зрізаної піраміди

8.

Чи вірно, що всі бічні грані правильної піраміди завжди є рівносторонніми трикутниками?

Ні

9.

Скільки основ має піраміда?

Одну

10.

Чи може висота піраміди дорівнювати висоті її бічної грані?

Не може

11.

Чи може основою правильної піраміди бути ромб?

Ніколи

12.

Чи в кожній піраміді можна побудувати діагональний переріз?

Ні, в трикутній не можна.

Тема: Паралелепіпед. Прямокутний паралелепіпед

№

Зміст запитання

Відповідь

1.

Що можна сказати про протилежні грані паралелепіпеда?

Паралельні і рівні

2.

Чи можуть всі діагоналі паралелепіпеда перетинатися в одній точці? Якщо так, то в якому випадку?

Так, завжди

3.

В якому паралелепіпеді діагоналі рівні?

Прямому прямокутному

4.

Чи може перерізом паралелепіпеда бути трикутник?

Так, може

5.

Який паралелепіпед називають прямокутним?

В основі прямокутник

6.

Якщо всі виміри паралелепіпеда рівні, як називають такий паралелепіпед?

Куб

7.

Який зв’язок існує між вимірами a, b.c ?          𝐷𝐵1 та довжиною відрізка

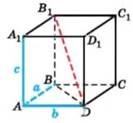
Квадрат діагоналі дорівнює сумі квадратів його лінійних вимірів

8.

Чи вірно,що точка перетину діагоналей паралелепіпеда ділить діагоналі паралелепіпеда навпіл?

Так

9.

Як називають переріз паралелепіпеда, котрий проходить через бічне ребро та діагональ основи?

Діагональний переріз

10.

Чи вірно, що основи паралелепіпеда різні .

Ні

11.

Чи можуть бічні грані похилого паралелепіпеда бути нерівними?

Можуть

12.

Чи можуть бічні ребра похилого паралелепіпеда бути нерівними?

Ні