Збірка математичних диктантів для учнів 11 класу по розділу: “Тіла обертання”

Тема:Циліндр

№

Зміст запитання

Відповідь

1.

Обертанням якої фігури навколо однієї із її сторін отримують циліндр?

Прямокутника

2.

Чи завжди можна отримати циліндр в результаті обертання паралелограма навколо однієї із його сторін? Якщо ні, то за якої умови циліндр можна отримати?

Не завжди Паралелограм є прямокутником

3.

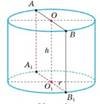
Побудуйте циліндр та вкажіть на малюнку такі його елементи:

а) вісь циліндра;

б) осьовий переріз:

в) радіус ОА

4.

Чи вірно, що площина, перпендикулярна висоті циліндра, утворює переріз циліндра, котрий є прямокутником?

Ні, перерізом буде круг

5.

З яких фігур складається розгортка циліндра. Зробіть малюнок розгортки циліндра.

Прямокутник, два круги

6.

Чи вірно, що всі твірні циліндра рівні між собою? Чи може твірна дорівнювати радіусу циліндра?

Твірні рівні завжди

R=H - може

7.

Яка фігура буде перерізом циліндра площиною, паралельною до основи циліндра?

Круг

8.

Записати формулу для обчислення площі бічної поверхні циліндра

𝑆 = 2π𝑅𝐻

9.

Чи існує площина, яка розбиває циліндр на два рівні циліндри. Якщо існує, як її побудувати?

Так. Посередині висоти, паралельно основі циліндра

10.

Скільки основ може мати циліндр?

Дві і тільки дві

11.

Кожен переріз циліндра є осьовим?

Ні

12.

Що являє собою переріз циліндра площиною, яка є паралельною осі циліндра? Зробіть малюнок.

Прямокутник

Тема:Конус

№

Зміст запитання

Відповідь

1.

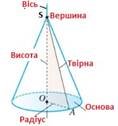
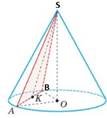
Побудуйте конус, на малюнку вкажіть основні його елементи: вершину, висоту, вісь, твірну, радіус, основу.

2.

Скільки радіусів має циліндр і скільки їх можна побудувати?

Радіус один, побудувати можна

безліч

3.

Чи може осьовим перерізом конуса бути рівносторонній трикутник?

Так, може

4.

Чи може висота конуса дорівнювати твірній? Якщо може, то в якому випадку.

Не може, ніколи

5.

Яка фігура лежить в основі конуса?

Круг

6.

Що називають радіусом конуса?

Радіус його основи

7.

Чи може трикутник перерізу бути рівнобедреним? Якщо може, то за якої умови?

Може, завжди

8.

Якщо твірна конуса 5 см, а висота 4 см. Чому дорівнює радіус основи?

3 см

9.

Яка фігура є перерізом конуса площиною, паралельною основі?

круг

10.

Висота осьового перерізу є висотою конуса?

Так

11.

Зробити малюнок зрізаного конуса та вказати на ньому висоту.

12.

Яка фігура є осьовим перерізом зрізаного конуса?

Рівнобічна трапеція

Тема:Куля і сфера

№

Зміст запитання

Відповідь

1.

Чи вірно, що кулю можна отримати в результаті обертання півкруга навколо його діаметра?

Так, вірно

2.

Чи можна говорити, що сфера- це поверхня кулі?

Так

3.

Що є великим кругом кулі?

Переріз кулі вздовж діаметра кулі

4.

Чи дорівнює радіус великого круга радіусу кулі?

Так, дорівнює

5.

Що можна сказати про відрізок, що сполучає центр кулі із центром перерізу кулі площиною?

ООперетину1 ⊥ до площини

6.

Чи вірно, що дотична до кулі площина завжди перпендикулярна до радіуса кулі, проведеного в точку дотику площини до кулі?

Так, завжди

7.

Як визначити площу сфери?

2

8.

Що можна сказати про відрізки дотичних, проведених до кулі з однієї точки?

𝑆Відрізки= 4π𝑅рівні _між

собою

9.

Що є геометричним місцем точок дотику прямих, які є дотичними до кулі, проведеними з однієї точки?

Коло

10.

Як називають переріз кулі площиною, що проходить через діаметр кулі?

Діаметральним перерізом або великим кругом

11.

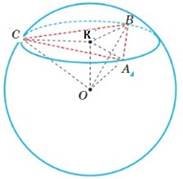
Якщо АВ=ВС=АС, що можна сказати про піраміду ОАВС?

Вона є правильною

12.

Обчислити площу поверхні кулі, радіус якої дорівнює 3 см.

2