Збірка математичних диктантів для учнів 11 класу по розділу: “Об’єми многогранників та тіл обертання. Площі поверхонь”

Тема:Об’єм призми та циліндра

№

Зміст запитання

Відповідь

1.

Закінчити речення:

Якщо тіло поділено на декілька частин, то його об’єм дорівнює…

сумі об’ємів його частинок

2.

Рівні тіла мають…

рівні об’єми

3.

Чому дорівнює об’єм куба, ребро якого дорівнює 5 см?

125 см²

4.

Чи достатньо знати площу основи призми та її висоту, щоб обчислити об’єм? Якщо так, напишіть виразом.

V= 𝑆0H

5.

Знайти об’єм прямокутного паралелепіпеда, якщо його лінійні виміри 2 см, 3 см, 5 см.

30 см3

6.

Що спільного мають формули для обчислення об’єму призми та циліндра?

Добуток площі основи на висоту

7.

Чи можна визначити радіус рівностороннього циліндра, якщо відомо його об’єм?

𝑉 = ³ 2^𝑉π

8.

Визначити ребро куба, об’єм якого дорівнює 64 ³

4 см

9.

Осьовий переріз рівностороннього циліндра  см 36 с ².Знайти об’єм циліндра.

54 см³

10.

Якщомциліндр вписано в куб, ребро якого дорівнює 1м. Знайти об’єм циліндра..

0,25π см³

11.

Обчислити об’єм призми, яку складено із трьох кубів, ребро яких доівнює 2 см

24 см³

12.

Знайти об’єм циліндра рівновеликого кубу, ребро якого дорівнює 3 см.

27      ³

Тема:Об’єм піраміди, конуса та кулі

№

Зміст запитання

Відповідь

1.

Об’єм якої просторової фігури дорівнює третині добутку площі основи на висоту?

Піраміди та конуса

2.

Знайти об’єм правильної чотирикутної піраміди, зі стороною основи 2 см, і висотою 3 см

4 см3

3.

Записати формулу для знаходження об’єму конуса та знайти об’єм конуса, якщо його висота 3 см, а радіус основи 1 см.

π см³

4.

Чи вірно, що об’єм кулі обчислюють за формулою 2?

Ні

5.

Якщо4π𝑅       конус та циліндр мають спільні основу і висоту. Що можна сказати про співвідношення їх об’ємів?

13

6.

Знайти об’єм кулі, радіус якої дорівнює 3 см.

36        ³

7.

SB=5cм; ОВ=4см

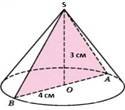
Знайдіть об’єм конуса.

16π см₃

πсм

8.

Намалюйте кулю, вписану в циліндр та знайдіть її об’єм, якщо висота кулі дорівнює 2 см.

43 π

9.

Об’єм конуса 48         ³. Знайдіть об’єм рівновеликої

йому кулі.             см

48см³

10.

Знайти об’єм правильної трикутної піраміди, сторона основи якої дорівнює    см, висота 4 см.

3см³

11.

Запишіть формулу для обчислення3    об’єму порожнистої кулі, якщо R- радіус зовнішньої стінки кулі, а r- радіус внутрішньої стінки.

V= 43 π(𝑅3 − 𝑟3)

12.

Знайти об’єм правильної чотирикутної піраміди із стороною основ 3 см та висотою 4 см.

12      ³

Тема: Площі поверхонь геометричних тіл

№

Зміст запитання

Відповідь

1.

Площа якої поверхні більша: куба, ребро якого дорівнює 1 см, чи правильної чотирикутної призми, площа основи якої дорівнює 1 ², а висота дорівнює стороні основи?            см

Рівні

2.

Обчислити повну поверхню прямокутного паралелепіпеда, площі граней якого дорівнюють

             2, 2      2                       2.

12 см²

3.

Знайти1 см площусм ; 3бічної см поверхні _{циліндра, радіус}

якого дорівнює 2 см , а висота 4 см.

16π см2

4.

Знайти повну поверхню рівностороннього циліндра, діаметр якого дорівнює 2 см.

⁶ πсм²

5.

Обчислити бічну поверхню правильної чотирикутної піраміди, в якої сторона основи дорівнює апофемі і дорівнює 4 см.

32 см²

6.

В скільки раз бічна поверхня циліндра більша за бічну поверхню конуса, якщо радіуси їх основ рівні, а висота циліндра дорівнює твірній конуса?

В 2 рази

7.

Чи може повна поверхня конуса дорівнювати поверхні куба?

Може

8.

Якщо ребро правильної трикутної піраміди дорівнює 2 см, то площа повної поверхні цієї піраміди дорівнює…

4 3 см2

9.

Що більше: площа сфери, радіусом 1 см, чи повна поверхня куба, ребро якого дорівнює 1 см.

І наскільки…?

⁽⁴π − 6) см²

10.

Якщо площа сфери дорівнює 16               Знайдіть її

радіус.                                                π см.

2 см

11.

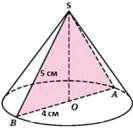
Обчислити бічну поверхню конуса, зображеного на малюнку.

20πсм2

12.

Записати формулу для обчислення площі сфери.

S=4