Збірник олімпіадних задач з математики для учнів 6 класу. Частина 12. Текстові задачі

Текстові задачі

1. Із жовтих, білих і червоних троянд склали букети. Яку найбільшу кількість букетів можна скласти, щоб у всіх букетах троянд кожного кольору було порівну?

2. У коробці лежать сині кульки і кілька червоних. Скільки червоних кульок у коробці, якщо ймовірність того, що вибрана навмання кулька:

а) виявиться синьою, дорівнює ;

б) виявиться червоною, дорівнює ?

3. У коробці було зелені і синіх кульок. Яку найменшу кількість кульок треба вийняти навмання, щоб ймовірність того, що серед вийнятих кульок хоча б одна буде зеленого кольору, дорівнювала ?

4. чоловік мали відремонтувати дорогу за днів. На п’ятий день їх спільної роботи вранці прибуло ще кілька чоловік, і решту роботи було виконано за днів. Скільки робітників прибуло додатково?

5. Є синіх і червоних листів паперу. Яке найбільше число комплектів можна скласти з цих листів для того, щоб в кожному комплекті було по однаковій кількості синіх і червоних листів?

6. На яблуні гілок, на кожній гілці по віток, на кожній віточці по яблук. Скільки всього яблук?

7. Для Івана, Ніни і Мишка купили яблука, які вони повинні були поділити порівну. Першим прийшов Іван: порахував яблука, взяв третю частину і пішов. Потім прийшла Ніна і зробила те саме. Нарешті, прийшов Мишко і взяв собі третю частину яблук, що залишились. Після чого залишилось яблук. Скільки яблук було куплено для трьох дітей?

8. Потрібно перевезти підручники. Відомо, що підручників більше ніж , але менше від . Якщо їх зав’язати в пачки по підручників у кожній, то залишаться підручники. Якщо ж зав’язати пачки по підручників у кожній, то також залишаться підручники. Якщо ж зав’язати пачки по підручників у кожній, то всі підручники будуть зав’язаними. Скільки книг потрібно перевезти?

9. Загін вишикували для походу в ряди по чоловік. Потім загін перебудували, поставивши по чоловік в кожен ряд. Якщо б загін перебудували ще раз, поставивши по чоловік в ряд, то в одному з рядів не вистачило б одного чоловіка. Скільки в загоні чоловік, якщо відомо, що їх більше , але менше ?

10. Вздовж дороги поставлені стовпці на відстані м один від іншого. Їх замінюють новими стовпцями, відстань між якими дорівнює м. Перший стовп ставлять на місце попереднього стовпця. Через скільки метрів від першого стовпця місця установки нових і старих стовпців будуть співпадати?

11. Як можна розділити груш між шістьма хлопчиками так, щоб не розрізати кожну більше, ніж на три частини?

12. В класі було учнів. Коли учнів вийшли з класу, то один учень сказав: „З класу вийшло всіх учнів”. Другий сказав, що вийшло всіх учнів і ще двоє. Яка відповідь правильна? Як ще можна сказати, скільки учнів вийшло?

13. Дві водопровідні труби діаметром по см кожна потрібно замінити однією трубою такою ж пропускною здатністю. Визначити діаметр цієї труби.

14. Мідну проволоку діаметром см витягнули так, що площа поперечного розрізу стала в рази менша. Який тепер діаметр має проволока?

15. Робітник виточив на станку з матеріалу дві кульки діаметрами см і см. У скільки разів маса другої кульки більше маси першої?

16. Роман і Дмитро записують дев’ятнадцятицифрове число, використовуючи тільки цифри , і . Першу цифру пише Роман, другу – Дмитро, третю – знову Роман і т. д. по черзі. Роман хоче отримати в результаті число, яке кратне . Чи може Дмитро завадити йому це зробити?

17. У класі вчиться менше учнів. За контрольну роботу з математики учнів отримали оцінку , учнів – оцінку , учнів – оцінку . Решта учнів, на жаль, отримали оцінку нижчу, ніж балів. Скільки учнів отримали оцінку нижче шести балів?

18. На футбольний матч „Динамо” – „Шахтар” з Донецька приїхало автобусів з уболівальниками. На стадіоні їх поділили на дві рівні групи. Скільки гостей приїхало, якщо усіх донецьких уболівальників не перевищує , а в кожному автобусі була однакова кількість пасажирів?

19. Група альпіністів за перший день подолала висоти гори, за другий – висоти, що залишилася, за третій – знову висоти, що залишилась, а за четвертий день альпіністи подолали решту м і досягли вершини. Знайдіть висоту цієї гори.

20. У чемпіонаті країни з футболу беруть участь команд, кожна з яких має свій стадіон. Усі команди повинні зіграти між собою, причому в кожному турі відбуваються всі ігор. Чи можна скласти розклад турів так, щоб кожна команда грала по черзі вдома та на виїзді?

21. Шаховий кінь починає свій маршрут у лівому куті дошки, а закінчує його в правому верхньому куті. Чи може кінь при цьому побувати на всіх полях дошки по одному разу?

22. Сім однакових буханців хліба потрібно розділити порівну між людьми. Як це виконати, не розрізаючи жодного буханця на рівних частин?

23. Як можна від шматка вірьовки довжиною дві третини метра відрізати шматок в півметра, не маючи жодних пристосувань для вимірювання?

24. В магазин привезли бочок, в яких було , , , , і декалітрів керосину. В перший день дві фірми закупили бочок, одна з них дві, а інша три бочки, причому виявилось, що перша закупила вдвічі менше керосину, ніж друга. Яка бочка залишилась в магазині?

25. Чи можна яблук розділити між хлопчиками порівну так, щоб не знадобилось жодного яблука розрізати більше, ніж на частини?

26. Як великих яблук розрізати порівну між хлопчиками, не розрізаючи жодного яблука більше, ніж на частини?

27. На чудо-дереві садівник виростив бананів і апельсинів. Кожного дня він зриває два плоди, і одразу на дереві виростає один новий. Якщо садівник зриває два однакових фрукти, то виростає апельсин, а якщо два різних – то банан. Яким виявиться останній фрукт на цьому дереві?

28. На полі розміром клітинок для гри у „морський бій” поставили корабель прямокутної форми розміром клітинки. Чи можна, зробивши постріли, гарантовано в нього влучити?

29. Із старовинної книги випала частина сторінок, які йдуть поспіль. Перша сторінка, що випала, має номер , а номер останньої записано тими самими цифрами в іншому порядку. Який номер останньої сторінки, що випала?

30. Сергій і Сашко по черзі беруть камінці з купи, у якій лежить камінців. За один хід кожному дозволяється брати або камінець, або . Хто з них візьме останній камінець, якщо гру починає Сергій?

31. Василь і Сашко грають у таку гру: вони по черзі (Василь першим) ламають шоколадку, що має клітинок. За один хід дозволяється зробити прямолінійний розлом будь-якого куска вздовж поглиблення між клітинками шоколадки. Програє той, хто в черговий раз не зможе цього зробити. Хто з них виграє?

32. В один ряд розміщено фішок. Будь-які дві фішки, розміщені через одну, дозволяється поміняти місцями. Чи можна переставити фішки у зворотному порядку?

33. Кожну грань куба пофарбовано в білий або чорний колір. Доведіть, що знайдуться дві грані зі спільним ребром, які пофарбовано в один колір.

34. Віктор купив зошит обсягом аркушів і пронумерував усі сторінки по порядку від до . Василь вирвав з цього зошита аркушів і додав усі чисел, які на них були написані. Чи могла отримана сума дорівнювати ?

35. В першій флязі молока в рази більше, ніж у другій. Коли з першої фляги перелили у другу л, молока в обох флягах стало порівну. Скільки літрів молока було в кожній флязі спочатку?

36. На столі лежать чотири чорні палички різної довжини, причому сума їх довжин дорівнює см, і п’ять білих паличок, сума довжин яких також дорівнює см. Чи можна розрізати ті й інші палички так, щоб потім розташувати їх парами, у кожній з яких довжини паличок будуть однаковими, а кольори різними?

37. Діти збирали в лісі гриби. Вийшовши з лісу, вони стали парами – хлопчик з дівчинкою, причому в хлопчика грибів або вдвічі більше, або вдвічі менше, ніж у дівчинки. Чи могло так статися, що всі діти разом зібрали грибів?

38. У клітинках таблиці розміром клітинок стоять нулі. Дозволяється вибрати будь-який квадрат розміром і збільшити числа в усіх його клітинках на одиницю. Чи можна отримати після кількох таких операцій таблицю, наведену на рисунку?

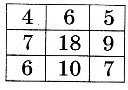
39. Футбольний м’яч щільно обтягнуті сіткою. З кожного вузла сітки виходять мотузки. Чи може в цій сітці бути вузлів?

40. Для Дмитрика, який захворів, лікар залишив шість зовні однакових пігулок – по дві кожного з трьох видів ліків. Дмитрику треба прийняти три пігулки вранці (по одній кожного виду) і три ввечері. Проте Дмитрик переплутав усі ліки. Чи зможе він виконати призначення лікаря?

41. Є кілька колод завдовжки м і м, загальна довжина яких дорівнює м. Яку найбільшу кількість розпилів може знадобитися зробити, щоб розпиляти всі колоди на чурбаки завдовжки м? (Кожним розпилом розрізається тільки одна колода).

42. Кожний учасник шахового турніру, граючи білими, виграв стільки партій, скільки всі інші разом, граючи чорними. Доведіть, що всі учасники здобули однакову кількість перемог.

43. У змаганнях з тенісу беруть участь гравців. Тенісист вибуває з турніру після першої поразки. Скільки зустрічей треба провести, щоб виявити переможця?

44. Доведіть, що в будь-якій компанії з осіб знайдеться троє попарно знайомих або троє попарно незнайомих.

45. У чемпіонаті України з футболу у вищій лізі беруть участь команд. Доведіть, що в будь-який момент чемпіонату є дві команди, які зіграли однакову кількість матчів. (Команди, які не зіграли жодного матчу, вважають такими, що зіграли їх однакову кількість).

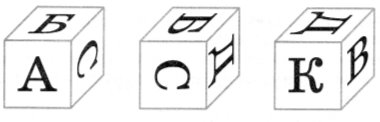
46. На рисунку зображено один і той самий кубик в різних положеннях. Яка буква написана на грані, протилежної до грані з літерою ?

47. Чотири хлопчики змагалися з кількох (більше одного) видів спорту. У кожному з видів спорту за одне й те саме місце нараховувалась однакова кількість балів (виражених натуральним числом), причому кожне з місць (, , , ) міг зайняти тільки один з учасників. Наприкінці цих змагань виявилося, що хлопчики здобули , , і балів відповідно. З’ясуйте, у скількох видах спорту вони змагались.

48. Населення України становить майже мільйонів чоловік. Доведіть, що є такий день у році, у який свій день народження святкують понад українців.

49. У країні Севентаун сім міст, кожне з яких сполучене шляхами більш ніж з двома містами. Доведіть, що з будь-якого міста можна дістатися до будь-якого іншого (можливо, проїжджаючи через інші міста).

50. У шаховій дошці розміром клітинок вирізали крайню ліву верхню і крайню праву нижню клітинки. Чи можна решту дошки замостити кісточками доміно, покриваючи однією кісточкою рівно дві клітинки дошки?

51. В одній купці лежить камінець, а в другій – камінці. За один хід дозволяється брати будь-яку кількість камінців, але тільки з однієї купки. Програє той, кому не буде чого брати. Хто виграє при правильній стратегії – той, хто починає, чи інший гравець?

52. Бабуся спекла торт для онуків, що мають приїхати до неї у гості на канікули. Але вона не знає точно, троє, п’ятеро чи шестеро онуків у неї гостюватимуть. Для того, щоб кожний внук отримав однакову частину торта, бабуся, передбачаючи всі три випадки, на скільки частин повинна розрізати торт?

53. Дві дівчинки і три хлопці з’їли разом порцій морозива. Кожен хлопець з’їв вдвічі більше порцій від кожної дівчинки. Скільки порцій з’їдять три дівчинки і два хлопці?

54. Йшли людей і несли буханців хліба. Кожен чоловік ніс по дві хлібини, кожна жінка – по половині хлібини, а кожна дитина – по чверті хлібини. Скільки йшло чоловіків, жінок і дітей?

55. Бібліотеці потрібно переплести книг. Одна майстерня може виконати цю роботу за днів, друга – за дні і третя – за днів. В який строк можуть виконати цю роботу три майстерні, працюючи одночасно, і скільки книг встигнуть переплести кожна з майстерень?

56. Косарі повинні були викосити дві галявини. Почавши вранці косити більшу галявину, вони після о півдня розділились: половина залишилась на першій галявині і до вечору її докосила, а інша половина перейшла косити іншу галявину, яка за площею вдвічі менша від першої. Скільки було косарів, якщо відомо, що на протязі наступного дня частину роботи, що залишилась, виконав один косар? 

57. Розділити яблук, що знаходяться у корзині, між п’ятьма друзями так, щоб кожний отримав по яблуку і одне яблуко залишилось у корзині.

58. Було аркушів паперу. Кожний з них розрізали на частин, потім деякі з отриманих частин знову розрізали на частин. Коли перерахували загальну кількість частин, то отримали частини. Довести, що обчислили провели невірно.

59. У дівчинки запитали: “Скільки грибів ти знайшла?”. Та відповіла: “Менше , і тому якби я їх розклала на купки по , або по , або по грибів, то в кожному випадку остачі не було б”. Скільки грибів знайшла дівчинка?

60. У змаганнях приймають участь учнів. На футболку кожного із учасників нанесено номер від до включно. Деяка фірма подарувала призи володарям тих номерів, котрі діляться на кожну з цифр в запису номера. Скільки учнів отримали призи?

61. На диво-дереві ростуть банани і ананаси. За один раз з дерева можна зірвати тільки два фрукти. Якщо зірвати два банани або два ананаси, то виростає один ананас, а якщо зірвати один банан і один ананас, то виростає один банан. Через деякий час на диво-дереві залишився один фрукт. Що це за фрукт, якщо спочатку на диво-дереві росло бананів і ананасів?

62. В сім’ї шестеро дітей, причому вік кожного з них в роках виражається простим числом. П’ятеро з них, відповідно, на , , , і років старші від наймолодшого. Скільки років наймолодшому?

63. З повної чашки кави відпили половину і долили стільки ж молока. Потім відпили третю частину кави з молоком і долили стільки ж молока. Потім відпили шосту частину кави з молоком і долили стільки ж молока. Після цього випили всю каву з молоком. Чого в результаті випили більше – кави чи молока?

64. Трьом учням в темній кімнаті наділи на голови чорні шапки. Перед ними поставили завдання: визначити, кому яку шапку наділи, якщо всього шапок було п’ять, причому дві з них – сірі, а три – чорні. Перед тим як увімкнути світло, сірі шапки заховали. Через деякий час один учень сказав, що він у чорній шапці. Як він розмірковував?

65. В гості до Кролика прийшли Вінні-Пух, П’ятачок і ослик Іа. Скількома способами Кролик може розсадити гостей на синю, червону і жовту табуретки?