ЗБІРНИК ЗАДАЧ З МАТЕМАТИКИ («Площі поверхонь» і «Об’єми тіл»)

 

 

 

 

 

 

 

 

 

 

 

 

 

ЗБІРНИК ЗАДАЧ З МАТЕМАТИКИ

 («Площі поверхонь» і «Об’єми тіл»)

Для учнів 11 класів.

Підготовка до З Н О.

 

 

 

 

 

 

Номінація: інноватика в організації

самостійної роботи учнів.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

                                                     Буча   2020.

       

 

 

 

 

 

Автор: В.І.Репенко, вчитель вищої категорії Бучанська Українська гімназія

 

 

 

 

 

Рецензент: С.С.Ковтун, доцент кафедри вищої математики НУБіП України.

 

 

 

 

Анотація: Пропонований збірник призначений для ефективного вивчення тем математики «Многогранники», «Двогранні кути», «Площі поверхонь» і «Об’єми тіл». Його структура і зміст завдань цілком відповідають вимогам чинної програми.

У збірнику міститься 238 задач, які пропонуються учням 11 класів для практичних занять і самостійного опрацювання, та довідковий матеріал для вивчення цих тем.

 

 

 

 

 

 

 

 

 

 

 

 

ЗМІСТ

Передмова	4
1. Задачі за темами Тема 1. Многогранники.  Двогранні кути та тригранні кути	5 5
Тема 2. Площа поверхні призми та піраміди. Зрізана піраміда та її поверхня	8
Тема 3. Піраміда. Перерізи піраміди	11
Тема 4. Розв’язування задач на обчислення площ поверхонь призми і піраміди	13
Тема 5. Тіла обертання: конус, циліндр та сфера.	15
Тема 6.Площа поверхні конуса, циліндра, сфери.	17
Тема 7. Розв’язування задач на комбінацію тіл.	20
Тема 8. Об’єми тіл, властивості об’ємів.  Об’єми призми та піраміди.	21
Тема 9. Обчислення площі поверхні та об’ємів повної і зрізаної піраміди	22
Тема 10. Обчислення об’ємів  многогранників	24
Тема 11.Обчислення об’ємів та поверхонь тіл обертання за допомогою  визначеного інтеграла. Об’єм циліндра	26
Тема 12.Конус, зрізаний конус. Об’єм і площа поверхні конуса та зрізаного конуса	28
Тема 13. Сфера, куля. Об’єм кулі та  її частин.  Площа сфери	29
Тема 14.Розв’язування задач на обчислення об’ємів тіл обертання	30
2. Довідковий матеріал	31
Використана література	44

 

 

 

 

 

 

 

 

 

 

Передмова

Глибокі й міцні знання з математики можна здобути, лише засвоївши основний теоретичний матеріал і розв’язавши достатню кількість вправ щодо його застосування.

Збірник задач з математики  при вивченні основних розділів стереометрії складено відповідно до чинної навчальної програми з математики, яка передбачає забезпечення шкільної математичної освіти на достатньому рівні.

Збірник може бути використаний для проведення практичних занять з математики, зокрема, при вивченні тем «Многогранники», «Двогранні кути», «Площі поверхонь» і «Об’єми тіл».

Видання містить задачі для самостійного опрацювання. Можливе використання його й на факультативних заняттях з математики.

 

1. ЗАДАЧІ ЗА ТЕМАМИ

Тема 1. Многогранники. Двогранні кути та тригранні кути

Задачі для класної  роботи

1.  У гранях  двогранного кута проведено прямі  а і b, паралельні його ребру, на відстані 10см і 6см від нього відповідно. Знайти величину цього двогранного кута, якщо відстань між прямими а і b дорівнює 14см.

2. Двогранний кут дорівнює 30°. Площина перетинає грані двогранного кута по паралельним прямим, віддаленим від ребра двогранного кута на 2√3 см і 6см. Знайти відстань від ребра двогранного кута до площини .

3.   Величина двогранного кута дорівнює 60°. На його ребрі вибрано точки А і В відстань між якими 24см , а у гранях - точки С і D такі, що AC = BC  = 13см, AD = BD = 15см. Знайти відстань між точками С і D.

4.  Двогранний кут дорівнює 45°. Дано точку на одній із граней кута. Відстань від цієї точки до другої грані кута – 12 см. Знайдіть відстань від даної точки до ребра двогранного кута.

5. Усередині двогранного кута, що дорівнює 30°, взято точку, віддалену від граней на 2 см і 3√3 см. Знайти відстань від цієї точки до ребра двогранного кута.

6. Всередині двогранного кута проведено пряму, паралельну його ребру. Знайдіть відстань між ребром кута і даною прямою, якщо двогранний кут дорівнює 30°, а відстані від даної прямої до граней кута дорівнюють 4 і 6√3см.

7. У тригранного кута два плоскі кути по 45°, двогранний кут між ними прямий. Знайдіть третій плоский кут. 

8.  Дано двогранний гострий кут α. З точки на ребрі даного кута в кожній з його граней проведено по променю. Відомо, що один з променів перпендикулярний до ребра кута, а інший утворює з ребром кут β. Знайдіть кут між даними променями.

9. Відрізки АВ і АС лежать у різних гранях двогранного кута. Знайдіть величину кута, якщо АВ= см, АС = 10см, ВС = 7см, а проекцією точок В і С на ребро двогранного кута є точка Д, віддалена від точки А на 6см.

10. У тригранного кута плоскі кути по 60°, а третій - 90°. Знайдіть кут між площиною прямого кута і протилежним ребром.

11. Через гіпотенузу прямокутного рівнобедреного трикутника проведено площину, яка утворює з площиною трикутника кут 45°. Знайдіть кути, які утворюють катети трикутника з цією площиною.

12. З точки А до площини α проведено похилі АВ і АС, які утворюють з площиною кути по 60°. Знайдіть відстань між точками В і С, якщо , а відстань від точки А до площини α дорівнює 3см.

 

Задачі для самостійного опрацювання

13. Двогранний кут дорівнює. Точка, яка належить одній з граней цього кута,  віддалена від другої грані на 4√2см. Знайдіть відстань від даної точки до ребра двогранного кута.

14. Відрізок АВ лежить в одній з граней двогранного кута, причому точка В лежить на ребрі кута. Знайдіть величину двогранного кута, якщо точка А віддалена від ребра кута на 4см, АВ=7 см, а його проекція на другу грань  дорівнює 3√5 см.

15. Площина γ перетинає грані двогранного кута, який дорівнює 60°, по  паралельних прямих, відстань між якими дорівнює 7см. Одна з прямих віддалена від ребра кута на 3см. Знайдіть відстань від ребра кута до другої прямої.

16. Всередині двогранного кута проведено пряму, паралельну його ребру. Знайдіть відстань між ребром кута і даною прямою, якщо двогранний кут дорівнює 30°, а відстань від даної прямої до граней кута дорівнюють 4 і 6√3см.

17. Визначте на рисунку (рис. 1) лінійний кут двогранного кута з ребром ВС, якщо у трикутника і  PA (ABC).

18.  Через сторону правильного трикутника проведено площину, яка утворює з площиною трикутника кут  30°. Знайдіть кути, які утворюють дві інші сторони трикутника з цією площиною.

19.  Визначте, чи можуть плоскі кути тригранного кута дорівнювати 60°,  20° і 30°. Відповідь поясніть.

20. Через сторону квадрата проведено площину, яка утворює з площиною квадрата кут 45°. Знайдіть кут між діагоналлю квадрата і цією площиною.

21. Точки А і В лежать на одній грані двогранного кута. Знайдіть величину цього кута, якщо точки А і В віддалені від другої грані на 6 і 8см, а точка В віддалена від ребра кута  на 4см дальше, ніж  точка А.

22. Дано двогранний гострий кут α. З точки на ребрі даного кута в кожній з його граней проведено по променю. Відомо, що обидва промені утворюють з ребром кути, рівні β, а кут між променями – гострий. Знайдіть кут між даними променями.

 

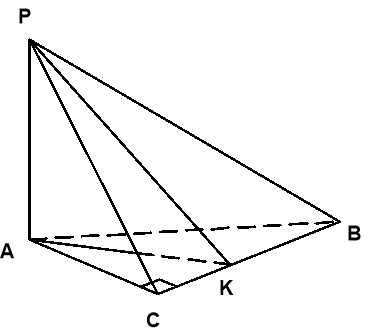
рис. 1

Тема 2. Площа поверхні призми та піраміди. Зрізана піраміда та її поверхня

Задачі для класної роботи

23. У похилій трикутній призмі відстані між бічними ребрами дорівнюють 5, 12, 9 см. Знайти бічне ребро призми, якщо бічна поверхня її дорівнює 260 см².

24. В похилій трикутній призмі дві бічні грані перетинаються під кутом 60° і мають рівні площі 24 см². Знайдіть бічну поверхню призми.

25. Обчисліть площу бічної поверхні правильної чотирикутної призми, діагональ якої дорівнює см і нахилена до площини основи під кутом 30º.

26. Основа прямої призми – трикутник зі стороною с і прилеглими до неї кутами α і β. Діагональ бічної грані, що проходить через сторону основи, яка протилежна куту α, нахилена до площини основи під кутом γ. Знайдіть висоту призми.

27. Основою прямого паралелепіпеда є ромб зі стороною а і гострим кутом α. Менша діагональ паралелепіпеда нахилена до площини основи під кутом β. Знайдіть площу бічної поверхні паралелепіпеда.

28. ABCA₁B₁C₁ - правильна зрізана піраміда (рис. 3) Перемалювати рисунок у зошит і побудувати: 1) кут нахилу бічного ребра до площини основи; 2) кут нахилу бічної грані до площини основи.

                                                       A₁                   B₁

                                                                        C₁

 

                                         A                                              B

 

                                С

(рис.3)

29. Основа правильної зрізаної піраміди дорівнюють 10см, 6см а бічне ребро утворює з площиною більшої основи кут 45°. Знайти площу діагонального перерізу піраміди.

30.У правильній зрізаній трикутній піраміді сторони основи дорівнюють 8см і 16см, а висота піраміди – 4см. Знайти площу бічної поверхні піраміди.

31.Сторона меншої основи правильної трикутної зрізаної піраміди дорівнює 2  см, а бічне ребро піраміди завдовжки √2 см утворює зі стороною більшої основи кут 45°. Знайдіть бічну поверхню зрізаної піраміди. Яку частину вона складає від бічної поверхні повної піраміди, з якої отримано дану зрізану піраміду?

32.Основа прямої призми – ромб з діагоналями 16см і 30см. Більша діагональ призми дорівнює 50см. Обчисліть площу бічної поверхні призми.

 

 

 

 

Задачі для самостійного опрацювання

33. Основа прямої призми – ромб з діагоналями 10см і 24см. Менша діагональ призми дорівнює 26см. Обчисліть площу бічної поверхні призми.

34. У похилій трикутній призмі  дві бічні грані взаємно перпендикулярні, а їх спільне ребро дорівнює 10см і знаходиться від інших бічних ребер на відстанях 5 і 12см. Знайдіть площу бічної поверхні призми.

35. Основою прямого паралелепіпеда є ромб зі стороною а і тупим кутом α. Більша діагональ паралелепіпеда нахилена до площини основи під кутом β.  Знайдіть площу бічної поверхні паралелепіпеда.

 

Тема 3. Піраміда. Перерізи піраміди

Задачі для класної роботи

36. Апофема правильної трикутної піраміди дорівнює 6см, а висота – 3см. Знайти площу бічної поверхні піраміди.

37. Сторона основи правильної чотирикутної піраміди дорівнює 6см. Знайдіть повну поверхню піраміди, якщо кут між апофемою та висотою піраміди дорівнює 30°.

38. Знайдіть площу бічної поверхні правильної трикутної піраміди, у якої бічне ребро дорівнює 10см, а апофема – 6см.

39. У правильній трикутній піраміді кут між апофемами дорівнює 60°. Знайти площу повної поверхні піраміди, якщо сторона її основи дорівнює 4см.

40. Основою піраміди АВCD є правильний трикутник АВС. Грань АВD перпендикулярна до площини основи. Відомо, що AD=BD=7, AB=8. Знайдіть довжину ребра CD.

41. В основі піраміди лежить прямокутний трикутник з кутом 30° і протилежним йому катетом, що дорівнює 30см. Бічні ребра нахилені до площини основи під кутом 60°. Знайдіть висоту піраміди.

42. Кожна бічна грань чотирикутної піраміди, в основі якої лежить квадрат, нахилена до основи під кутом 60°. Площа основи піраміди 16 . Знайдіть площу бічної поверхні піраміди.

43.Основою піраміди є трикутник зі сторонами 13, 20 і 21см. Знайдіть висоту піраміди, якщо двогранні кути при основі дорівнюють по 30°.

44. Побудувати переріз трикутної піраміди SABC площиною, яка проходить через площину S точку на ребрі АС і паралельну прямій BC.

45.Побудуйте переріз піраміди SABC площиною, яка проходить через точки M, N, K – середини ребер SB, BC, AC відповідно.

46. Побудуйте переріз тетраедра SABC площиною, яка проходить через ребро SC і точку перетину медіан грані АВС.

47. Основа чотирикутної піраміди SABC – квадрат  ABCD.  Всі ребра піраміди дорівнюють а.  Побудуйте переріз піраміди, який проходить через точку В і середину ребра SA паралельно ребру SC. Визначте вид побудованого перерізу і знайдіть його площу.

48. Основа піраміди – квадрат зі стороною 9см, а суміжні бічні грані перпендикулярні до площини основи. Обчисліть площу бічної поверхні піраміди, якщо середнє за довжиною бічне ребро піраміди дорівнює 15см.

49. Основа піраміди – трикутник зі сторонами 13см, 14см і 15см. Знайдіть площу перерізу, який проходить паралельно площині основи і ділить висоту піраміди у відношенні 1:2, рахуючи від вершини піраміди.

 

 

 

Задачі для самостійного опрацювання

50. Знайти площу бічної поверхні правильної чотирикутної піраміди, бічне ребро якої дорівнює 8см, а висота - 4см.

51. Дано трикутну піраміду SABC (рис. 2). Побудуйте: а) точку перетину прямої MN і площини АВС; б) лінію перетину площин ANC і SBC.

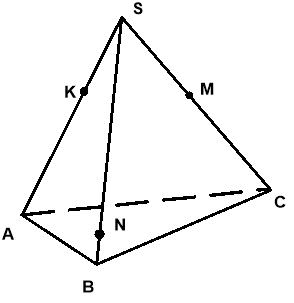
рис. 2

52. Основою піраміди КМNF є трикутник MNF, <MFN=90º, <FMN=30º, MN=12 см. Бічна грань MKF перпендикулярна до площини основи, а дві інші нахилені до неї під кутом 45º. Знайдіть довжину ребра KF.

53. Основою піраміди     SABC є трикутник зі сторонами АС = 13см, АВ = 15см, СВ = 14см. Бічне ребро SA перпендикулярне до площини основи і дорівнює 9см. Знайдіть площу повної поверхні піраміди.

54. Основа чотирикутної піраміди SABC – квадрат  ABCD.  Всі ребра піраміди дорівнюють а.  Побудуйте переріз піраміди, який проходить через точку В і середину ребра SAпаралельно ребру SC. Визначте вид побудованого перерізу і знайдіть його площу.   

55. В правильній чотирикутній піраміді сторона основи дорівнює 6см, а апофема – 4см. Знайдіть: а) бічне ребро піраміди;  б) висоту піраміди;  в) повну поверхню піраміди.

56.  Скільки всього граней у піраміди, основою якої є шестикутник?

57. Бічне ребро правильної чотирикутної піраміди дорівнює 8см і утворює з площиною основи кут 60º. Знайдіть площу бічної поверхні піраміди.

58. Основою піраміди МАВС є трикутник АВС, <АСВ=90º, <ВАС=60º, см. Бічна грань ВМС перпендикулярна до площини основи, а дві інші нахилені до неї під кутом 30º. Знайдіть довжину ребра МС.

59. Сторона основи правильної  трикутної піраміди дорівнює 8см, а бічна грань нахилена до площини основи під кутом 30º. Знайдіть площу повної поверхні піраміди.

60. Обчисліть площу бічної поверхні правильної чотирикутної призми, діагональ якої дорівнює 8√2см і нахилена до площини основи під кутом 45°.

 61. Основа прямої призми – трикутник зі стороною а, протилежним цій стороні кутом α і прилеглим  кутом β. Діагональ бічної грані, яка містить сторону основи, до якої прилягають кути α і β, нахилена до площини основи під кутом γ. Знайдіть висоту призми.

 

Тема 4. Розв’язування задач на обчислення площ поверхонь призми і піраміди

Задачі для класної роботи

62. Діагональ куба дорівнює 6 см. Знайдіть площу повної поверхні куба.
63. Ребро куба дорівнює а. Знайдіть діагональ.
64. Діагональ куба дорівнює 7. Знайдіть його повну поверхню.
65. Знайти повну поверхню куба за відомою площею S його діагонального перерізу.
66. Діагональ прямокутного паралелепіпеда дорівнює d і утворює з площиною однієї бічної грані кут α, а іншої – кут β. Знайдіть площу бічної поверхні паралелепіпеда.
67. Основа прямої призми – ромб з гострим кутом α. Діагональний переріз призми, що проходить через більшу діагональ основи, має площу S. Знайдіть площу бічної поверхні призми.
68. Основа піраміди – квадрат зі стороною 12 см, а дві суміжні бічні грані перпендикулярні до площини основи. Обчисліть площу бічної поверхні піраміди, якщо її висота дорівнює 5 см.
69. У правильній трикутній призмі 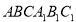сторона основи дорівнює 8 см, а бічне ребро – 2 см. Через сторону АС нижньої основи і середину сторони 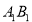верхньої проведено площину. Знайдіть площу перерізу.
70. В правильній трикутній піраміді двогранний кут при основі дорівнює α. Відстань від основи висоти піраміди до її апофеми дорівнює l. Знайдіть бічну поверхню піраміди.
71. Основа піраміди – рівнобедрений трикутник з бічною стороною 5 см і основою 6 см. Всі двогранні кути при основі піраміди дорівнюють 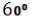. Знайдіть повну поверхню піраміди.
72. Основа прямої  призми – рівнобедрений прямокутний трикутник, катет якого дорівнює 5 см. Кут між діагоналями рівних бічних граней, які проведені з однієї вершини верхньої основи, дорівнює 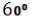. Обчисліть площу бічної поверхні призми.

 

Задачі для самостійного опрацювання

73.  Ребро куба 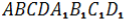дорівнює 2 см. Чому дорівнює площа трикутника ?
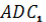74. Діагональ основи куба дорівнює а. Чому дорівнює діагональ куба?
75. Діагональ прямокутного паралелепіпеда дорівнює d і утворює з площиною основи кут α, а з площиною бічної грані – кут β. Знайдіть площу бічної поверхні  паралелепіпеда.
76.  У правильній чотирикутній призмі 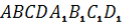  сторона  основи дорівнює 4 см, а бічне ребро – 3 см. Через діагональ BD нижньої основи і середину сторони 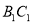верхньої проведено площину. Знайдіть площу перерізу.
77.  Основа піраміди – прямокутний трикутник з катетами 6 і 8 см. Всі двогранні кути при основі піраміди дорівнюють 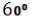. Знайдіть повну поверхню піраміди.
78.  Основа прямої призми – рівнобедрений трикутник з бічною стороною 8 см і кутом 120° при вершині. Кут між діагоналями рівних бічних граней, які проведено з однієї вершини верхньої основи, дорівнює 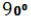. Обчисліть площу бічної поверхні призми.

 

Тема 5. Тіла обертання: конус, циліндр та сфера.

Задачі для класної роботи

79. Радіус основи циліндра дорівнює 4 см, висота 6 см. Знайти діагональ осьового перерізу.
80. Площа осьового перерізу циліндра дорівнює 20 см, а площа основи дорівнює 4π 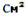. Знайти висоту циліндра.
81. Висота циліндра дорівнює 6 см, радіус основи дорівнює 5 м. Знайти площу перерізу, проведеного паралельно осі циліндра на відстані 4 м від неї.
82. Паралельно до осі циліндра проведено площину, яка відтинає від кола основи дугу 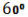. Радіус циліндра дорівнює 6 см. Знайдіть площу отриманого перерізу, якщо висота циліндра дорівнює 5 см.
83. Діаметр основи конуса дорівнює 6 см, а висота дорівнює 4 см. Знайти твірну конуса.
84. У рівнобічному конусі (в осьовому перерізі – правильний трикутник) радіус основи дорівнює R. Знайти площу перерізу, проведеного через дві твірні, кут між якими дорівнює 30°.
85. Твірна конуса дорівнює к і нахилена до площини основи під кутом α. Знайдіть: а) висоту конуса; б) радіус основи конуса; в) площу основи; г) площу осьового перерізу; д) відстань від центра основи конуса до твірної.
86. Відношення площі основи конуса до площі осьового перерізу дорівнює π. Знайдіть кут нахилу твірної до основи.
87. Радіус основи конуса дорівнює 28 см, а твірна довша висоти на 8 см. Знайдіть площу осьового перерізу конуса.
88. Твірна конуса дорівнює а. Знайти площу перерізу, проведеного через дві твірні, кут між якими дорівнює α.
89. Твірна конуса дорівнює l. Радіус основи дорівнює r. Знайдіть площу перерізу, проведеного через вершину конуса і хорду основи, що стягує дугу, кутова величина якої дорівнює α.
90. Радіус кулі дорівнює 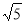см. Всередині чи зовні кулі розміщена точка А, якщо вона віддалена: 1) від центра кулі на 2см; 2) від центра кулі на 2,3см; 3) від точки на  поверхні кулі на 4,5см?
91.  Площа великого круга даної кулі дорівнює Q, а площа перерізу площиною дорівнює 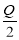. На якій відстані від центра кулі проведено переріз?
92. Кулю радіуса 5 см перетнуто площиною на відстані 3 см від центра. Знайдіть площу перерізу.
93. Радіус сфери дорівнює 15 см. Знайдіть довжину кола перерізу, віддаленого від центра сфери на 12 см.

 

 

 

Задачі для самостійного опрацювання

94. Осьовий переріз циліндра – квадрат, площа якого 100 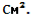Знайти площу основи циліндра.
95. Площа основи циліндра дорівнює 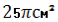 , а довжина твірної – 24 см. Знайдіть діагональ осьового перерізу.
96. Паралельно до осі циліндра на відстані 2 см від неї проведено площину, яка відтинає від кола основи дугу 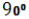. Знайдіть площу отриманого перерізу, якщо висота циліндра дорівнює 6 см.
97. Бічну поверхню рівностороннього циліндра (осьовий переріз – квадрат) з висотою 4 см розрізали по твірній. Знайдіть площу отриманої розгортки.
98. Твірна конуса дорівнює 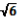м і нахилена до площини основи під кутом 45°. Знайти площу повної поверхні циліндра.
99. Переріз конуса, що проходить через його вершину, утворює з площиною основи кут β і відтинає від кола основи дугу α. Висота конуса дорівнює Н. Знайдіть площу перерізу.
100. Кулю перетнуто площиною на відстані 6 см від центра. Площа перерізу дорівнює 64π 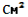. Знайдіть радіус кулі.
101. Кулю перетнули площиною на відстані 12 см від її центра. Площа утвореного перерізу дорівнює 25π 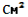. Знайдіть довжину радіуса кулі.

Тема 6. Площа поверхні конуса, циліндра, сфери.

Задачі для класної роботи

102. Відрізок, що сполучає центр верхньої основи циліндра з точкою кола нижньої основи, дорівнює 6 см. Знайдіть площу бічної поверхні циліндра, якщо його висота дорівнює діаметру основи.
103. У нижній основі циліндра проведено хорду, яку видно з центра цієї основи під кутом 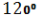, а з центра верхньої основи – під кутом 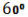. Знайдіть площу бічної поверхні циліндра, якщо довжина хорди становить 6 см.

104.  У циліндрі паралельно його осі проведено площину, що перетинає нижню основу циліндра по хорду, яку видно з центра цієї основи під кутом α. Діагональ утвореного перерізу нахилена до площини основи під кутом β. Знайдіть площу бічної поверхні циліндра, якщо площа його основи дорівнює S.

105. В основі конуса проведено хорду, яку видно із центра основи під кутом α, а із вершини конуса – під кутом β. Знайдіть площу бічної поверхні конуса, якщо радіус основи дорівнює R.

106.Через вершину конуса проведено площину, яка перетинає основу по хорді, довжина якої дорівнює а. Ця хорда стягує дугу, градусна міра якої дорівнює . Кут між твірними в перерізі дорівнює . Знайдіть площу бічної поверхні конуса.

107. Катет прямокутного трикутника дорівнює а, а прилеглий кут дорівнює α. Знайдіть площу бічної поверхні конуса, утвореного при обертанні цього трикутника навколо даного катета.

108. Через дві твірні конуса, кут між якими дорівнює α, проведено переріз, який утворює з площиною основи конуса кут β. Знайдіть площу бічної поверхні конуса, якщо його висота дорівнює Н.

109. У кулі на відстані 12 см від її центра проведено переріз, площа якого дорівнює . Знайдіть площу поверхні кулі.

110. Через кінець радіуса кулі проведено переріз, який утворює з цим радіусом кут .. Знайдіть площу поверхні кулі, якщо площа перерізу дорівнює .

111.  Хорду нижньої основи циліндра видно із центра цієї основи під кутом α. Відрізок, що сполучає центр верхньої основи із серединою даної хорди, нахилений до площини основи під кутом β. Знайдіть площу бічної поверхні циліндра, якщо радіус основи дорівнює R.

112.  Діагональ осьового перерізу циліндра дорівнює 12 см. Знайдіть площу бічної поверхні циліндра, якщо його висота дорівнює діаметру основи.

113.  Діагональ прямокутника дорівнює d і утворює з його більшою стороною кут α. Знайдіть площу бічної поверхні циліндра, утвореного обертанням даного прямокутника навколо його меншої основи.

      

Задачі для самостійного опрацювання

114. У циліндрі паралельно його осі проведено площину, що перетинає нижню основу циліндра по хорді, яку видно з центра цієї основи під кутом α. Знайдіть площу бічної поверхні циліндра, якщо площа утвореного перерізу дорівнює S.

115. В основі конуса проведено хорду завдовжки а, яку видно із центра основи під кутом α, а з вершини конуса – під кутом β. Знайдіть площу бічної поверхні конуса.

116. Кут при вершині осьового перерізу конуса дорівнює α, а відстань від центра основи до твірної конуса дорівнює а. Знайдіть площу бічної поверхні конуса.

117. Pадіус основи конуса дорівнює 2√5 см, а відстань від центра його основи до твірної – 4см. Знайдіть площу бічної поверхні конуса.

118. Через дві твірні конуса проведено площину, яка нахилена до площини його основи під кутом α. Ця площина перетинає основу конуса по хорді, яку видно із центра його основи під кутом β. Знайдіть площу бічної поверхні конуса, якщо його твірна дорівнює m.

119. Переріз кулі площиною, яка віддалена від її центра на 15см, має площу . Знайдіть площу поверхні кулі.

120. Довжина лінії перетину сфери і площини, яка віддалена від її центра на 12см, дорівнює 10π см. Знайдіть площу сфери.

121. Хорду нижньої основи циліндра видно із центра цієї основи під кутом α. Відрізок, що сполучає центр верхньої основи із серединою даної хорди, нахилений до площини основи під кутом β. Знайдіть площу бічної поверхні циліндра, якщо твірна циліндра дорівнює l.

 

Тема 7. Розв’язування задач на комбінацію тіл.

Задачі для класної роботи

122. У нижній основі циліндра проведено хорду, яку видно із центра цієї основи під кутом α. Відрізок, що сполучає центр верхньої основи з одним із кінців проведеної хорди, утворює з площиною основи кут β. Знайдіть площу бічної поверхні циліндра, якщо відстань від центра нижньої основи до проведеної хорди дорівнює а.

79. Чи можна описати циліндр навколо прямої призми, в основі якої лежить прямокутник?
80. Визначити вид трикутника, який лежить в основі призми, вписаної в циліндр, якщо вісь циліндра  проходить поза призмою.
81. Основа прямої призми – квадрат з діагоналлю 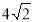см. Повна поверхня призми дорівнює 112 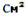. Знайдіть площу осьового перерізу циліндра, вписаного в дану призму.
82. В циліндр з радіусом R і висотою Н вписано правильну трикутну призму. Знайдіть бічну поверхню призми.
83. У конус вписано правильну чотирикутну піраміду. Висота і радіус конуса відповідно дорівнюють 1 і 2 см. Знайдіть: а) бічне ребро піраміди; б) сторону основи піраміди; в) апофему піраміди; г)  площу основи піраміди; д) площу бічної поверхні піраміди.
84. Бічне ребро правильної трикутної піраміди і сторона основи відповідно дорівнюють 5 і 6 см. У дану піраміду вписано конус. Знайдіть : а) твірну конуса; б) радіус основи конуса; в) висоту конуса.
85. Бічне ребро правильної чотирикутної піраміди, описаної навколо конуса, дорівнює l, а плоский кут при вершині піраміди - 2α. Знайдіть: а) твірну конуса; б) сторону основи піраміди; в) радіус основи конуса; г) висоту конуса.

Задачі для самостійного опрацювання

130. Чи можна вписати призму в циліндр, в основі якого лежіть ромб?

131. Основа прямої призми – прямокутник зі сторонами 6 і 8 см. Діагональ призми утворює з площиною основи кут . Знайдіть площу осьового перерізу циліндра, описаного навколо призми.

132. Навколо циліндра з радіусом R і висотою Н описано правильну трикутну призму. Знайдіть бічну поверхню призми.

133. Бічне ребро правильної трикутної піраміди і сторона основи відповідно дорівнюють 5 і 6 см. У дану піраміду вписано конус. Знайдіть : а) площу бічної поверхні піраміди; б) площу осьового перерізу конуса.

134. Бічне ребро правильної чотирикутної піраміди, описаної навколо конуса, дорівнює l, а плоский кут при вершині піраміди - 2α. Знайдіть площу бічної поверхні піраміди.

 

Тема 8. Об’єми тіл, властивості об’ємів.

Об’єми призми та піраміди.

Задачі для класної роботи

135. В основі прямої призми лежить рівнобедрений трикутник, основа якого дорівнює 12см, а висота, проведена до неї, - 8см. Знайдіть об'єм призми, якщо її висота дорівнює 10см.

136.  В основі прямої призми лежить трапеція з основами 9 і 15см і висотою 5см. Знайдіть об'єм призми, якщо її бічне ребро дорівнює 10см.

137. Сторона основи правильної чотирикутної призми дорівнює 5см, а діагональ бічної грані - 13см. Знайдіть об'єм призми.

138. грані трикутної піраміди мають площі 36см², і 48см² і утворюють кут 150°. Знайти об'єм призми, якщо її бічне ребро дорівнює 12см.

139. Бічне ребро похилої трикутної призми дорівнює 6см, дві бічні грані її взаємно перпендикулярні і мають площі 24 см² і 30 см². Знайдіть об'єм призми.

140.  У правильній чотирикутній піраміді висота дорівнює 3см, бічне ребро - 5см. Знайдіть об'єм піраміди.

141. Сторона основи правильної трикутної піраміди дорівнює 4см, висота піраміди дорівнює 6√3 см. Знайдіть об'єм піраміди.

 

Задачі для самостійного опрацювання

142.  В основі прямої призми лежить трикутник, сторона якого дорівнює 12см, а висота, проведена до неї, - 5см. Бічне ребро призми дорівнює 8см. Знайдіть об'єм призми.

143. Основа прямої призми - рівнобедрений трикутник з бічною стороною 5см і периметром 18см. Знайдіть об'єм призми, якщо одна її бічна грань - квадрат.

144.  Бічне ребро правильної трикутної піраміди дорівнює 5см, висота – 4см. Знайдіть об'єм піраміди.

145.  Усі грані призми - рівні ромби зі стороною 8см і гострим кутом 60°. Знайти об'єм призми.

Тема 9. Обчислення площі поверхні та об’ємів повної і зрізаної піраміди

Задачі для класної роботи

146. Знайдіть об'єм правильної трикутної піраміди,  сторона її основи дорівнює 6см, а бічне ребро утворює з площиною основи кут .

147. Апофема правильної чотирикутної піраміди дорівнює l, двогранний кут при основі дорівнює α. Знайдіть повну поверхню та об'єм піраміди.

148.  Бічне ребро правильної трикутної піраміди дорівнює b і утворює з площиною основи кут β. Знайдіть об'єм піраміди.

149.  Основою піраміди є трикутник із сторонами 5, 5 і 6см. Кожна бічна грань нахилена до площини основи під кутом . Знайдіть об'єм піраміди.

150.  Бічною гранню правильної зрізаної чотирикутної піраміди є трапеція, більша основа якої дорівнює 8см, а менша основа і бічні сторони – по 4см. Знайдіть об'єм даної зрізаної піраміди.

151.  Знайдіть об'єм правильної чотирикутної зрізаної піраміди, висота якої дорівнює 3см, а радіуси кіл, описаних навколо основ, і см.

 

Задачі для самостійного опрацювання

160.  Сторона основи правильної трикутної піраміди дорівнює 6см, а двогранний кут при основі піраміди - . Знайдіть повну поверхню та об'єм піраміди.

161.  Бічною гранню правильної зрізаної чотирикутної піраміди є трапеція, більша основа і бічні сторони якої дорівнюють по 6см, а менша основа – по 4см. Знайдіть об'єм даної зрізаної піраміди.

162.  Сторона основи правильної зрізаної чотирикутної піраміди дорівнює 2см і 6см, а площа бічної поверхні у два рази більша за суму площ її основ. Знайдіть об'єм піраміди.

163.  Сторони основ правильної зрізаної трикутної піраміди дорівнюють 3см і 6см, а висота повної піраміди 10см. Знайти об'єм зрізаної піраміди.

        

 

 

Тема 10. Обчислення об’ємів  многогранників

Задачі для класної роботи

164.  В основі прямої призми лежить прямокутний трикутник із катетами 6 і 8 см. Висота призми дорівнює 10 см. Знайдіть об'єм призми.

165.  Основа піраміди – ромб з більшою діагоналлю 12 см і гострим кутом . Всі двогранні кути при основі піраміди дорівнюють . Знайдіть об'єм піраміди.

166.  В основі піраміди лежить рівнобедрений трикутник з кутом при основі і бічною стороною 12 см. Усі бічні ребра піраміди утворюють з площиною основи кут . Знайдіть об'єм піраміди.

167.  Знайдіть об'єм куба, діагональ якого дорівнює d.

168.  Знайдіть об'єм куба, площа грані якого дорівнює Q.

169.  Площі трьох граней прямокутного паралелепіпеда дорівнюють 6 ,  6 , 9 . Знайдіть його об'єм.

170.  Діагональ бічної грані прямокутного паралелепіпеда дорівнює 5√2 см. Діагональ паралелепіпеда утворює з площиною цієї грані кут , а з площиною основи – кут . Знайдіть об'єм паралелепіпеда.

171. Основа прямої призми – прямокутний трикутник з катетом а і протилежним кутом α. Діагональ бічної грані, що містить гіпотенузу, нахилена до площини основи під кутом β. Знайдіть об'єм призми.

172.  В основі прямої призми лежить рівнобедрений трикутник з кутом α при вершині. Діагональ грані, що містить бічну сторону трикутника, дорівнює d і утворює з площиною основи кут β. Знайдіть об'єм призми.

173.  Основа прямої призми – прямокутний трикутник з катетами 3 і 4 см. Діагональ бічної грані, яка містить гіпотенузу трикутника, дорівнює 13 см. Знайдіть об'єм призми.

174.  Основа прямої призми – ромб з гострим кутом . Діагональ бічної грані дорівнює 8 см і утворює з площиною основи кут  . Знайдіть об'єм призми.

175. Діагональ куба дорівнює а. Чому дорівнює об'єм куба?

176. Площі двох граней правильної трикутної призми дорівнюють і      см? Знайдіть об'єм призми.

177.  Сторони основ правильної чотирикутної піраміди дорівнюють 2 см і 4 см, а гострий кут бічної грані . Знайдіть об'єм піраміди.

178.  Основою піраміди є рівнобедрений трикутник, у якого бічна сторона дорівнює а, а кут при вершині дорівнює φ. Усі бічні ребра нахилені до площини основи під кутом γ. Знайдіть об'єм піраміди.

179.  Основа прямого паралелепіпеда – ромб з периметром 40 см. Бічне ребро паралелепіпеда дорівнює 9 см, а одна з його діагоналей – 15 см. Знайдіть об'єм паралелепіпеда.

180.  В правильній трикутній піраміді двогранний кут при основі дорівнює α. Знайдіть об'єм піраміди, якщо відстань від середини її висоти до апофеми дорівнює d.

 

Задачі для самостійного опрацювання

181.  В основі піраміди лежить рівнобедрений трикутник з основою 12 см і кутом при вершині. Усі бічні ребра піраміди утворюють з площиною основи кут . Знайдіть об'єм піраміди.

182.  Знайдіть об'єм куба, діагональ грані якого дорівнює d.

183.  Знайдіть об'єм куба, площа діагонального перерізу якого дорівнює S.

184.  Периметри трьох граней прямокутного паралелепіпеда дорівнюють 10 см,  14 см, 16 см. Знайдіть об'єм паралелепіпеда.

185.  Діагональ прямокутного паралелепіпеда дорівнює 6 см і утворює з бічними гранями кути і . Знайдіть об'єм паралелепіпеда.

186.  Основа прямої трикутної призми – рівнобедрений трикутник з кутом α при основі. Діагональ бічної грані призми, що містить бічну сторону основи, дорівнює l і нахилена до площини основи під кутом β. Знайдіть об'єм призми.

187.  Основа прямої призми – прямокутний трикутник з гіпотенузою с і гострим кутом α. Діагональ бічної грані, що містить катет, протилежний куту α, нахилена до площини основи під кутом β. Знайдіть об'єм призми.

188.  Периметри двох граней правильної трикутної призми дорівнюють 30 і 48 см. Знайдіть об'єм призми.

189.  Основа прямого паралелепіпеда – ромб з периметром 40 см. Одна з діагоналей ромба дорівнює 12 см.  Знайдіть об'єм паралелепіпеда, якщо його більша діагональ дорівнює 20 см.

190.  В правильній трикутній піраміді бічні ребра нахилені до площини основи під кутом α. Відстань від середини висоти піраміди до бічного ребра дорівнює d. Знайдіть об'єм піраміди.

 

Тема 11. Обчислення об’ємів та поверхонь тіл обертання за допомогою визначеного інтеграла. Об’єм циліндра

Задачі для класної роботи

191. Знайдіть об'єм тіла, утвореного при обертанні квадрата навколо його сторони, яка дорівнює а.

192.  Осьовий переріз циліндра - квадрат, діагональ якого дорівнює l. Знайдіть об'єм циліндра.

193.  Діагональ осьового перерізу циліндра утворює з твірною кут α. Знайдіть об'єм циліндра, якщо радіус основи циліндра дорівнює R.

194. Площа осьового перерізу циліндра дорівнює 8, кут між діагоналлю перерізу і площиною основи дорівнює α. Знайдіть об'єм циліндра.

195.  Хорда основи циліндра дорівнює 16 см і віддалена від центра цієї основи на 6 см. Відрізок, що сполучає центр іншої основи циліндра з кінцем даної хорди, утворює з площиною основи кут 45°. Знайдіть об'єм циліндра.

196. В основі циліндра проведено хорду, яку видно із центра цієї основи під кутом β. Відстань від центра цієї основи до хорди дорівнює d. Відрізок, який з'єднує центр однієї основи з точкою кола другої основи, утворює з площиною основи кут α. Знайдіть об'єм циліндра.

197. У нижній основі циліндра проведено хорду, яку видно з центра цієї основи під кутом 120°, а з центра верхньої основи - під кутом 60°. Знайдіть площу бічної поверхні циліндра, якщо довжина хорди становить 6 см.

 

Задачі для самостійного опрацювання

198. Осьовий переріз циліндра - квадрат зі стороною а. Знайдіть об'єм циліндра.

199. Знайдіть об'єм циліндра, якщо розгортка його бічної поверхні - квадрат зі стороною а.

200. Радіус основи циліндра дорівнює R, площа осьового перерізу - S. Знайдіть об'єм циліндра.

201. Діагональ осьового перерізу циліндра утворює з основою кут α. Знайдіть об'єм циліндра, якщо його висота дорівнює Н.

202. У циліндрі, паралельно його осі проведено площину. Вона перетинає основу по хорді, яку видно із центра цієї основи під кутом α. Діагональ утвореного перерізу дорівнює d і нахилена до основи під кутом β. Знайдіть об'єм циліндра.

Тема 12. Конус, зрізаний конус. Об’єм і площа

поверхні конуса та зрізаного конуса

Задачі для класної роботи

203. Висота конуса дорівнює 6 см, твірна - 10 см. Знайдіть об'єм конуса.

204. Із центра основи конуса проведено перпендикуляр до твірної, який утворює з висотою кут β. Знайдіть об'єм конуса, якщо його твірна дорівнює l.

205. Хорда основи конуса дорівнює а і стягує дугу α. Відрізок, який з'єднує вершину конуса із серединою хорди, нахилений до основи під кутом β. Знайдіть об'єм конуса.

206. Хорда основи конуса видна з центра основи під кутом α, а з вершини конуса - під кутом β. Знайдіть об'єм конуса, якщо відстань від центра його основи до середини твірної дорівнює d.

207. Осьовим перерізом конуса є рівнобедрений прямокутний трикутник, площа якого дорівнює а². Знайти об'єм конуса.

208. В основі конуса проведено хорду завдовжки 8√2 см на відстані 4см від центра основи. Знайдіть об'єм конуса, якщо його твірна нахилена до площини основи під кутом 60°.

209. Радіус основи конуса дорівнює R, а його осьовий переріз - прямокутний трикутник. Знайдіть об'єм конуса.

210. Радіуси основ зрізаного конуса дорівнюють 2 і 5 см. Один з кутів осьового перерізу конуса дорівнює 135°. Знайдіть об'єм конуса.

211. Радіуси основ зрізаного конуса дорівнюють 3 і 6, а твірна дорівнює 5. Знайти його об'єм.

212. Висота зрізаного конуса дорівнює 3 см. Радіус однієї основи вдвічі^; більший радіуса другої основи, а твірна нахилена до площини основи під кутом 45°. Знайдіть об'єм зрізаного конуса.

 

 

 

Задачі для самостійного опрацювання

213. Осьовий переріз конуса - рівнобедрений трикутник, один з кутів якого дорівнює 120°. Знайдіть об'єм конуса, якщо його висота дорівнює 4 см.

214. Площа повної поверхні конуса дорівнює 200π см², а його твірна - 17 см. Знайдіть об'єм конуса.

215. Гіпотенуза прямокутного трикутника дорівнює l, а один із гострих кутів дорівнює α. Знайдіть об'єм конуса, утвореного при обертанні цього трикутника навколо катета, протилежного даному куту.

216. Об'єм зрізаного конуса дорівнює 584π см³, а радіуси основ - 10 см і 7 см. Знайдіть висоту конуса.

217.  Площина, яка проходить через вершину конуса, утворює з площиною основи конуса кут β. Хорда, по якій дана площина перетинає основу конуса, стягує кут α. Знайдіть об'єм конуса, якщо відстань від його вершини до даної хорди дорівнює l.

 

Тема 13. Сфера, куля. Об’єм кулі та  її частин.  Площа сфери

Задачі для класної роботи

218. Радіус кулі дорівнює 9 см. Знайдіть об'єм кулі.

219. Об'єм кулі дорівнює 36л см². Знайдіть радіус кулі.

220. Довжина кола перерізу, який проходить через центр кулі, дорівнює 8π см. Знайдіть об'єм кулі.

221. Переріз кулі, віддалений від її центра на 3 см, має площу 16л см². Знайдіть об'єм кулі.

222. Знайдіть об'єм кульового сектора, якщо радіус кулі дорівнює 6 см, а висота сектора - 2 см.

223. В кулі, об'єм якої дорівнює 288π см³, проведено переріз. Відрізок, що сполучає центр кулі з точкою кола даного перерізу, утворює з площиною перерізу кут 60°. Знайдіть площу перерізу.

224. Радіус кулі дорівнює R. Знайдіть об'єм кульового сектора, якщо дуга у його осьовому перерізі дорівнює 90°.

225. Через кінець радіуса кулі проведено переріз, який утворює з цим радіусом кут 30°.  Знайдіть площу поверхні кулі, якщо площа перерізу дорівнює 36π см².

Задачі для самостійного опрацювання

226.  Знайдіть об'єм кулі, діаметр якої дорівнює 12 см.

227.  На відстані 4 см від центра кулі проведено переріз, довжина кола якого дорівнює 6π см. Знайдіть об'єм кулі.

228.  Знайдіть об'єм кульового сегмента, якщо радіус кулі дорівнює 8 см, а висота сегмента – 3 см.

229.  Радіус кулі дорівнює R. Знайдіть об'єм кульового сегмента, якщо його діаметр дорівнює радіусу кулі.

 

Тема 14. Розв’язування задач на обчислення об’ємів тіл обертання

Задачі для класної роботи

230.  Переріз, паралельний до осі циліндра, перетинає його основу по хорді, яка дорівнює а, що стягує кут α. Діагональ перерізу складає з твірною циліндра кут β. Знайдіть об'єм циліндра.

231.  Діаметр перерізу, віддаленого від центра кулі на см, дорівнює 4 см. Знайдіть площу поверхні та об'єм кулі.

232.  Хорда нижньої основи циліндра дорівнює а і видна з центра цієї основи під кутом α. Знайдіть об'єм циліндра, якщо відрізок, що сполучає центр верхньої основи з одним з кінців даної хорди, утворює з площиною основи кут β.

233.  Прямокутний трикутник з катетом 3 см і протилежним до нього кутом обертається навколо даного катета. Знайдіть повну поверхню тіла обертання.

234.  Через дві твірні конуса, кут між якими дорівнює α, проведено переріз, що перетинає основу конуса по хорді завдовжки а. Знайдіть об'єм конуса, якщо кут між його твірною і висотою дорівнює β.

Задачі для самостійного опрацювання

235.  На відстані 4 см від центра кулі проведено переріз, діаметр якого дорівнює 6 см. Знайдіть площу поверхні та об'єм кулі.

236.  Хорда нижньої основи циліндра дорівнює а і видна з центра цієї основи під кутом α. Знайдіть бічну поверхню циліндра, якщо відрізок, що сполучає центр верхньої основи з серединою даної хорди, утворює з площиною основи кут β.

237.  Прямокутний трикутник з катетом 3 см і прилеглим до нього кутом обертається навколо другого катета. Знайдіть об'єм тіла обертання.

238.  Твірна конуса нахилена до площини його основи під кутом β. Хорда основи конуса завдовжки а видна з його вершини під кутом α. Знайдіть повну поверхню конуса.

 

2. ДОВІДКОВИЙ МАТЕРІАЛ

 

Многогранники. У стереометрії вивчають фігури у просторі, які називаються тілами. Наочно (геометричне) тіло можна уявити як частину простору, зайняту фізичним тілом і обмежену поверхнею.

   Многогранник – це таке тіло, поверхня якого складається із скінченної кількості плоских многокутників. Многогранник називається опуклим, якщо він лежить по один бік від площини кожного з плоских многокутників на його поверхні. Спільна частина такої площини і поверхні опуклого многогранника називається гранню. Грані опуклого многогранника є плоскими опуклими многокутниками. Сторони граней називаються ребрами многогранника, а вершини - вершинами многогранника.

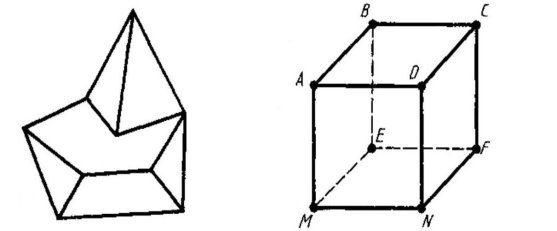
Двогранні кути.  Двогранним кутом називається фігура, утворена двома півплощинами із спільною прямою, що їх обмежує. Півплощини називаються гранями, а пряма, що їх обмежує,- ребром двогранного кута.

 Площина,  перпендикулярна до ребра двогранного кута,перетинає його грані по двох пів прямих. Кут, утворений цими півпрямими, називається лінійним кутом двогранного кута. За міру двогранного кута приймається міра відповідного йому лінійного кута. Усі лінійні кути двогранного кута суміщаються паралельним перенесенням, а отже, вони рівні. Тому міра двогранного кута не залежить від вибору лінійного кута.

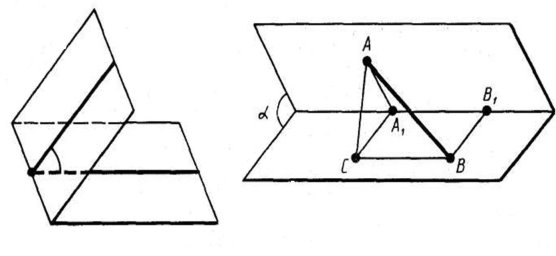
Тригранні кути. Розглянемо три промені а, b, c, які виходять з однієї точки і не лежать в одній площині. Тригранним кутом (abc) називається фігура, яка складається з трьох плоских кутів (ab), (bc), і (ac). Ці кути називаються гранями тригранного кута, а їх сторони – ребрами. Спільна вершина плоских кутів називається вершиною тригранного кута. Двогранні кути, утворені гранями тригранного кута, називаються двогранними кутами тригранного кута. 

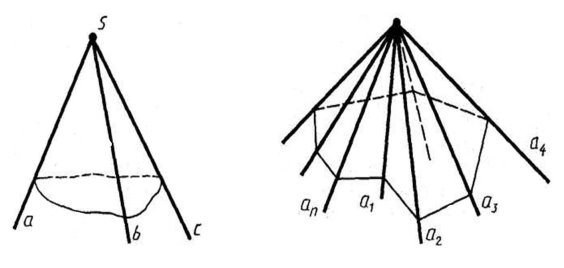
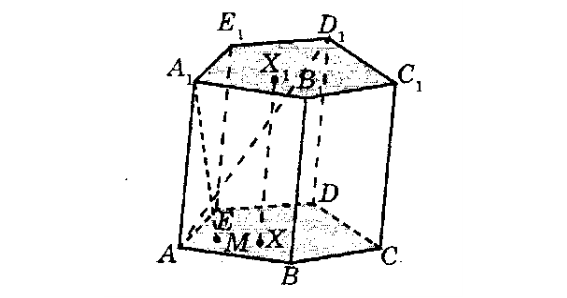
Призма

 

Довільна призма. Призмою називають многогранник, що складається з двох плоских многокутників, які лежать у різних площинах і суміщаються паралельним перенесенням, та всіх відрізків, що сполучають відповідні точки цих многокутників.

ABCDE і A₁B₁C₁D₁E₁ – основи призми

AA₁, BB₁, … - бічні ребра

ABB₁A₁, BCC₁B₁. … - бічні грані

 

1.  Основи призми рівні:

     ABCDE = A₁B₁C₁D₁E₁

 

2.  Основи призми лежать у паралельних площинах:

     пл. ABCDE || пл. A₁B₁C₁D₁E₁

 

3.  Бічні ребра призми паралельні й рівні:

     AA₁ || BB₁|| CC₁ …,

     AA₁= BB₁ =CC₁ …

 

4.  Вічні грані призми – паралелограми:

     ABB₁A₁  паралелограм

     BCC₁B₁ паралелограм

 

5 . V_призми = S_осн * H_призми

 

6.  S_бічн = P_{перп. перерізу} * AA₁

(S _бічн =S _ABB1A1 +  S_BCC1B1 + …)

 

АD₁ — діагональ призми — сполучає дві вершини призми, що не належать одній грані. Висота призми — відстань між площинами її основ

Пряма призма. Призму називають прямою, якщо її бічні ребра перпендикулярні до основ.

AM  пл. ABCDE; A₁M  = H  висота

 

 

1. Основи призми рівні:

    ABCDE = A₁B₁C₁D₁E₁

 

2. Основи призми лежать у паралельних площинах:

    пл. ABCDE || пл. A₁B₁C₁D₁E₁

 

3. Бічні ребра призми паралельні і рівні:

   АА₁ || BB₁|| CC₁ …,

   АА₁ = BB₁= CC₁ …

 

4. Бічні грані призми  паралелограми:

   ABB₁A₁  паралелограм;

   BCC₁B₁  паралелограм, …

 

5. V_призми = S_осн. * H_призми

 

6. S_бічн. = P_{перп. перерізу} * AA₁

   (S_бічн. =S_ABB1A1 +S_BCC1B1 + …+ S_AEE1A1)

 

7. S_повна = S_бічн. + 2S_осн

 

 

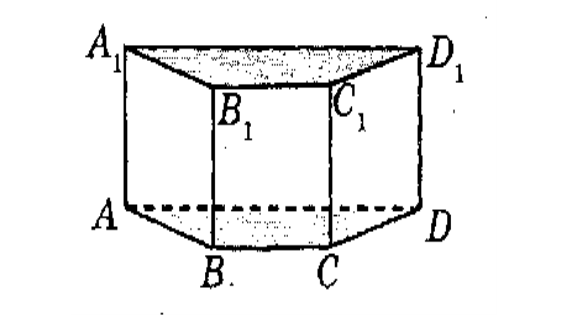
1. Висота прямої призми дорівнює бічному ребру:

   H _{прямої призми}  = AA₁ = BB₁= …

 

2. Бічні грані прямої призми  прямокутники:

    ABB₁A₁  прямокутник;

    BCC₁B₁  прямокутник, …

 

3. V_{прямої призми} = S_осн. *H = S_осн. AA₁

 

4. S_бічна = P_осн.AA₁

 

5. S_повна = S_бічна + 2S_осн.

 

                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                       

Паралелепіпед.

Довільний паралелепіпед

 

 

Паралелепіпедом називають призму, в основі якої лежить паралелограм.

1. У паралелепіпеда всі грані — паралелограми.

2. У паралелепіпеда протилежні грані паралельні й рівні.

3. Діагоналі паралелепіпеда перетинаються в одній точці і точкою перетину діляться навпіл.

О  середина діагоналей A₁C B₁D AC₁ B₁D

 

Прямокутний паралелепіпед

Прямий паралелепіпед, у якого осно­вою є прямокутник, називають пря­мокутним паралелепіпедом.

 

 

 

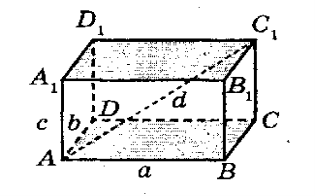
1. У прямокутного паралелепіпеда всі грані  прямокутники.

 

2. d² =a²+b²+c², або AC₁² +AB² +AD² +AA₁²

У прямокутному паралелепіпеді квадрат будь-якої діагоналі дорівнює сумі квадратів трьох його вимірів.

 

3.  V_{прямокут. паралелеп}  AB*AD*AA₁ = abc

 

4. S_бічн.  = P_осн. * AA₁ = 2(AB+ AD)* AA₁ =  2(a+b)c

 

5. S_повна = S _бічн. + 2S_осн.

 

Куб

Кубом називають прямокутний паралелепіпед, у якого всі ребра рівні.

 

 

 

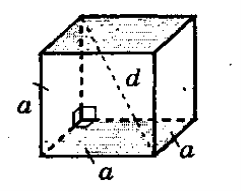
1. У куба всі грані  квадрати.

 

2. d = a3,

де d  діагональ куба,

d² =  a²  + a²  + a² , де а  ребро куба

 

3. V_куба =  a³

 

4. S_бічн.= 4a² ;

S_повна=6a²

 

                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                  

Піраміда. Довільна піраміда

 

 

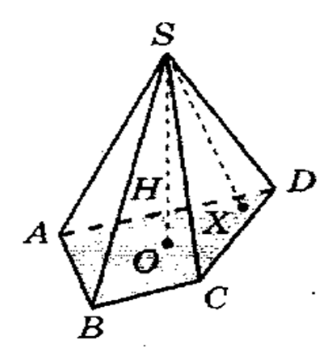
Пірамідою називають многогранник, який складається з плоского многокутника (основи піраміди), точки, яка не лежить у площині основи (вершини піраміди), і всіх від­різків, що сполучають вершину піраміди з точками основи.

 

            Трикутна                                                            Чотирикутна

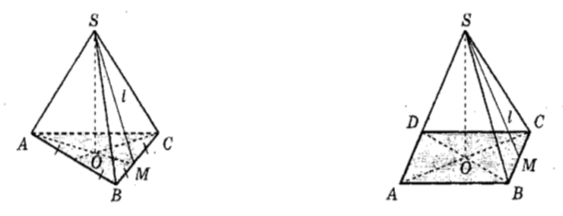
  ABC  правильний                    ABCD  квадрат

О  точка перетину медіан (висот і бісектрис),         O  точка перетину діагоналей

       центр вписаного й описаного кіл

 

Піраміду називають правильною, якщо її основою є правильний многокутник, а основа висоти збігається з центром цього многокутника.

SO  висота правильної піраміди

(SO  пл.ABC;  O  центр основи)

SM  апофема правильної піраміди  висота бічної грані  (SM  BC)

 

1. У правильній піраміді бічні ребра рівні й однаково нахилені до площини основи:

SA = SB = SC = …

 SAO  = SBO  = SCO = …

 

2. Бічні грані правильної піраміди  рівні між собою рівнобедрені трикутники, однаково нахилені до площини основи.

 

3. S_бічн.= P_осн. * SM =  P_осн. * l, де l  апофема.

 

4. S_бічн.=  , де  =  SMO   кут нахилу всіх бічних граней до основи;

S_бічн.=  S_{бічн. грані} * n, де n   кількість граней.

 

5. S_повна =  S_бічн. +  S_осн.

 

6. V_пір = S_осн *H

 

 

ABCD  основа піраміди; SA, SB, SC, SD  бічні ребра

 ASB,  BSC,  CSD, ASD  бічні грані

 

SO пл. ABC

 

S_бічн = S_ASB + S_BSC + S_CSD +S_ASD

 

V_{пір =} S_осн *H

 

S_повна = S_бічн + S_осн

 

 

 

Циліндр

 

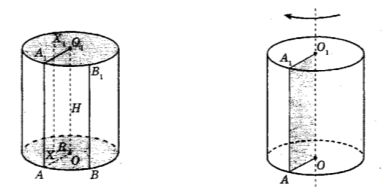
Циліндром (круговим циліндром) називають тіло, що складається з двох кругів, які не лежать в одній площині й суміщаються паралельним перенесенням, і всіх відрізків, які сполучають відповідні точки цих кругів. Круги — основи циліндра.

 

Відрізки, що сполучають відповідні точки кіл кругів,— твірні;

Циліндр називають прямим, якщо його твірні перпендикулярні до площин основ. У шкільних підручниках:

циліндр = прямий круговий циліндр

 

1. Основи циліндра рівні і паралельні:

OA = O₁A₁ = R;  пл. AOB || пл.  A₁O₁B₁ ,

де О  центр нижньої основи циліндра; О₁ центр верхньої основи

 

2. Твірні циліндра паралельні й рівні: AA₁ || BB₁, AA₁ = BB₁

 

3. Висота циліндра (відстань між площинами основ) дорівнює твірній:

H_цил = AA₁ =  OO₁

 

4. Під час обертання прямокутника навколо його сторони як осі утворюється циліндр: OAA₁O₁  прямокутник; ОО₁  вісь утвореного циліндра;

R_{утв. цил.} = OA = O₁A₁, H_цикл = OO₁ = AA₁

 

5. S_осн = R2; S_бічн = 2RH; S_повна = S_бічн + 2S_осн = 2R (H+R)

 

6. V_цил = S_осн *H = R²H

 

 

Конус

 

 

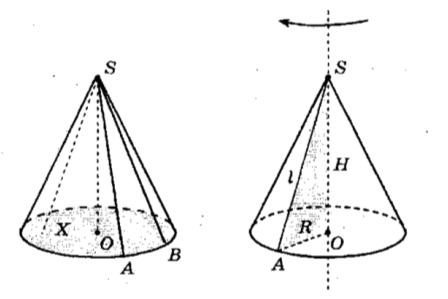
Конусом (круговим конусом) називають тіло, що складається з круга, точки, яка не лежить у площині цього круга, і всіх відрізків, що сполучають дану точку з точками круга.

 

Круг — основа конуса.

 

Відрізки, що сполучають вершину конуса з точками основи,  твірні.

SA, SB  твірні конуса.

Конус називають прямим, якщо SO   пл.AOB (O  центр круга основи).

У шкільних підручниках:

конус = прямий круговий конус

 

1. Твірні конуса рівні: SA = SB = …

 

2. H_кон =  SO (SO || пл. AOB)

 

3. Під час обертання прямокутного трикутника навколо його катета як осі утворюється конус:  AOS прямокутний,  AOS = 90⁰, пряма SO  вісь конуса, R _{осн. кон} = AO,  H_кон = SO,  AS  твірна,  AS = l.

 

4. S_{осн. кон} = R²;  S_{бічн. кон} = Rl;  S_повна = S_бічн + S_осн = R (l + R)

 

5. V_кон =    S_осн *H =   R²H

 

Сфера та куля.

Сфера

 

O  центр сфери;

OA  радіус сфери,  OA = R

S_сфери = 4R²

 

Сферою називають поверхню, яка складається з усіх точок простору, що розташовані на даній відстані (В) від даної точки (О).

 

Куля

                                          O – центр кулі

                                                         OB – радіус кулі, OB=R

                                V= R²

 

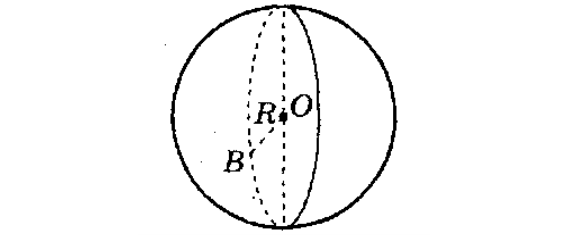
Кулею називають тіло, що складається з усіх точок простору, що розташовані на відстані, не більшій за дану (Н), від даної точки (О).

Переріз кулі площиною

 

Будь-який переріз кулі площиною є кругом.

Центр цього круга — основа перпендикуляра, опущеного з центра кулі на січну площину.

V= R³

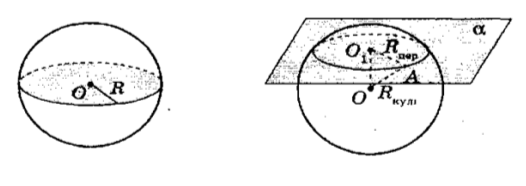
O центр кулі

O₁  центр круга перерізу; ОО1  .

Із  OO₁A: AO₁ = R R OO

R_пер  =  R² _кулі – ОО₁²

Переріз, що проходить через центр кулі,  великий круг.

R_{вел. круга} = R_кулі

 

 

 

 

 

 

Використана література

1. Бевз Г.П. Математика 10-11.  – К.: «Бліц» - 2005.
2. Бурда М.І., Біляніна О.Я., Вашуленко О.П., Прокопенко Н.С. Збірник завдань для державної підсумкової атестації з математики. Книга 1, книга 2. – Х.: «Гімназія» - 2008.
3. Мерзляк А.Г., Полонський В.Б., Рабінович Ю.М., Якір М.С. Збірник задач і завдань для тематичного оцінювання з геометрії для 11 класу. – Х.: «Гімназія» - 2001.
4. Нелін Є.П., Роганін О.М. Математика. Збірник завдань для ЗНО. – Х.: «Гімназія» - 2010.
5. Погорєлов О.В. Геометрія 10-11. – К.: «Освіта»-2001.